Сбалансированные деревьяЕсли элементы вставляются в дерево бинарного поиска с помощью алгоритма выполнения вставки, рассмотренного нами в предыдущей теме, то структура дерева зависит от порядка, в котором вставляются записи. Если записи вставляются в отсортированном порядке или в порядке, обратном отсортированному, то результирующее дерево будет иметь все левые (или правые) связи пустыми, так что поиск по дереву сводится к последовательному поиску (скорость n/2). Для последовательности 1, 3, 5, 7, 8, 12 дерево будет выглядеть следующим образом.
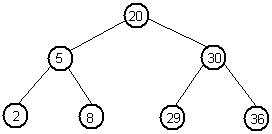
Если, однако, записи вставляются так, что половина записей, вставленных после любой заданной записи с ключом k, имеют ключи меньше, чем k, а половина записей имеют ключи больше чем k, то получается некоторое сбалансированное дерево, в котором для извлечения элемента достаточно выполнить примерно LOG2n сравнений ключей. Для последовательности 20, 30, 5, 8, 29, 36, 2 дерево будет выглядеть следующим образом. Поэтому время, необходимое для поиска по дереву бинарного поиска, изменяется в диапазоне от LOG2n в лучшем случае до n/2 в худшем. Для дерева из 256 вершин количество сравнений при поиске может находиться в диапазоне от 8 до 128, что является очень большим разбросом.
Таким образом степень баланса зависит от последовательности, в которой ключи вставляются в это дерево. Следовательно, двоичное дерево представляет интерес, только если оба поддерева всякой вершины почти равновесны. В этом случае каждый этап операции просмотра или включения делит примерно надвое размер двоичного дерева, которое еще остается просмотреть. Однако, рассмотренные на предыдущей лекции алгоритмы вставки и удаления не гарантируют нам сохранения равновесности в дереве. Поэтому хотелось бы иметь некоторый алгоритм эффективного поиска, вставки и удаления, который сохранял бы дерево в равновесном, сбалансированном состоянии. Давайте определим точный термин "сбалансированное дерево". Высотой (глубиной) некоторого бинарного дерева является максимальный уровень его листьев. Высоту пустого дерева будем определять как -1. Баланс некоторого узла определяется как высота его левого поддерева минус высота его правого поддерева. Сбалансированным бинарным деревом является такое бинарное дерево, у которого абсолютное значение баланса каждого узла меньше или равно 1. Рассмотрим пример сбалансированного бинарного дерева. Каждый узел в таком дереве имеет баланс, равный 1, -1 или 0, в зависимости от того, что высота его левого поддерева больше, меньше или равна высоте его правого поддерева.
Постановка задачи балансировки Предположим, что задано некоторое сбалансированное бинарное дерево и мы использует алгоритм поиска и вставки, рассмотренный на предыдущей лекции, чтобы вставить новый узел в данное дерево. Тогда результирующее дерево может остаться сбалансированным, а может и не остаться им. Очевидно, что дерево становится несбалансированным, если только заново вставляемый узел является левым потомком некоторого узла, который ранее имел баланс, равный 1, или если он является правым потомком некоторого узла, который ранее имел баланс, равный -1. Если после включения новой вершины баланс дерева нарушен, то необходимо найти самый нижний разбалансированный узел. Далее рассмотрим поддерево, имеющее корень в самом младшем предке, который стал несбалансированным в результате некоторой вставки. Рассмотрим случай, где баланс этого поддерева ранее был 1 (для -1 все рассуждения аналогичны). Назовем несбалансированный узел узлом A. Поскольку баланс этого узла – 1, то его левое поддерево непусто. Следовательно, мы можем обозначить его левого потомка как узел B. Так как узел A является самым младшим предком, который стал несбалансированным из-за нового узла, то узел B должен иметь баланс, равный 0 (рассмотреть, почему это так). Таким образом, узел B должен иметь до вставки левое и правое поддеревья равной высоты n (возможно n=-1). Поскольку баланс узла A был 1, то правое поддерево A должно также быть высотой n (вышеизложенное рассмотреть на рисунке).
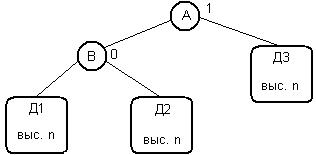
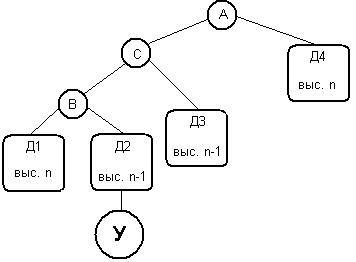
Теперь надо рассмотреть два случая. В первом случае узел вставляется в левое поддерево, изменяя баланс узла B на 1, а баланс узла A на 2 (Рис. 1).
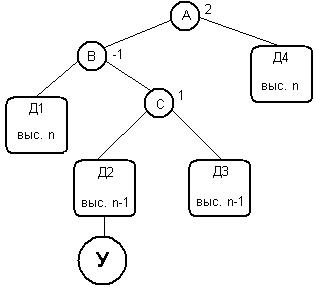
Во втором случае узел вставляется в правое поддерево B, изменяя баланс узла B на -1, а баланс узла A на 2 (Рис. 2). Пусть узел C будет сыном узла B. Имеется три случая – узел C может быть заново вставляемым узлом, и в этом случае n=-1, или заново вставляемый узел может быть в левом или правом поддереве узла C. Рассмотрим случай, когда вставляемый узел находится в левом поддереве узла C. В остальных двух случаях балансировка выполняется аналогично.
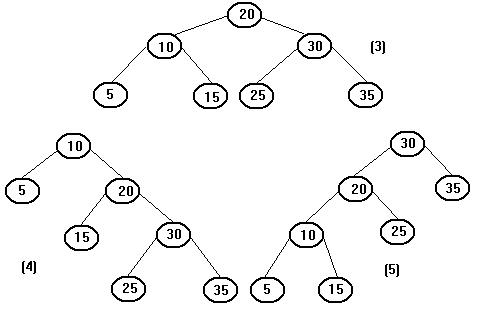
Чтобы получить сбалансированное дерево, необходимо выполнить некоторую трансформацию данного дерева так, чтобы выполнялись следующие условия: 1. Прохождение трансформированного дерева в симметричном порядке должно быть таким же, как для первоначального дерева (т.е. трансформированное дерево должно оставаться деревом бинарного поиска). 2. Трансформированное дерево должно быть сбалансированным. Решение первого условия Сначала поищем пути решения первой проблемы. Найдем способы изменения дерева таким образом, чтобы оно оставалось деревом бинарного поиска. Рассмотрим следующие деревья.
Дерево, представленное на рисунке (4), будет некоторым правым поворотом дерева (3). Аналогичным образом говорят, что дерево, представленное на рисунке (5), будет некоторым левым поворотом дерева (3). Как видно из рисунков, получаемые в результате поворотов деревья остаются деревьями бинарного поиска. Кроме того, при прохождении всех трех деревьев методом "слева направо" порядок узлов сохраняется (5, 10, 15, 20, 25, 30, 35). Рассмотрим алгоритм выполнения левого поворота для некоторого поддерева, где Work1 – указатель на корень этого поддерева (алгоритм правого поворота аналогичен). 1. Work2 = Work1->PRP 2. Work3 = Work2->PLP 3. Work2->PLP = Work1 4. Work1->PRP = Work3 Конечно, при любом повороте значение указателя на корень поддерева, для которого осуществляется поворот, также должно быть изменено, чтобы указывать на новый корень. В случае левого поворота новый корень в вершине, на который указывает Work2. Так как при любом повороте порядок узлов сохраняется и дерево остается деревом бинарного поиска, то для получения некоторого сбалансированного дерева может быть выполнено любое число левых или правых поворотов без нарушения первого из рассмотренных выше условий. Решение второго условия Вернемся теперь к рисункам 1 и 2. Для рисунка 1 выполним правый поворот для поддерева с корнем в узле A. Результирующее дерево будет иметь следующий вид.
Отметим, что полученное дерево дает такое же прохождение методом "слева направо" и является сбалансированным. Кроме того, поскольку высота исходного поддерева (1) до вставки была равна n+2, а высота результирующего поддерева после вставки также равна n+2, то баланс каждого предка узла A в первоначальном дереве остается неизменным. Таким образом, замена поддерева (1) на поддерево с правым поворотом гарантирует, что сохраняется сбалансированное дерево бинарного поиска. Рассмотренный выше поворот еще называют LL-поворотом. Для балансировки дерева (2) необходимо выполнить два поворота: левый поворот поддерева с корнем в узле B, и правый поворот поддерева с корнем в узле A. После выполнения левого поворота получим следующее дерево.
А после выполнения правого поворота получим дерево.
Отметим, что полученное дерево дает такое же прохождение методом "слева направо" и является сбалансированным. Высота дерева (2) до вставки была равна n+2, как и высота сбалансированного поддерева. Следовательно, балансировка не повлияла на баланс вершин, находящихся выше вершины A. Рассмотренный выше случай балансировки называется двойным RL-поворотом. RR- и RL-повороты выполняются аналогично. Каждый из четырех поворотов уникально определяется балансом вершин, участвующих в повороте (см. таблицу).
|