Собственные числа и собственные векторы матрицыПриведем основные определения и теоремы, необходимые для решения практических задач вычисления собственных чисел и собственных векторов матриц. Определение 3.5. Собственным числом (или собственным значением) квадратной матрицы A называется число λ такое, что система уравнений A x = λ x (3.35) имеет ненулевое решение x. Это решение называется собственным вектором матрицы A, соответствующим собственному значению λ. Собственный вектор определяется с точностью до постоянного множителя, — если x удовлетворяет (3.35), то и c x также является решением (3.35). Преобразуем систему (3.35) к виду (A – λ E) x = 0, где E — единичная матрица. Так как система линейных однородных уравнений имеет ненулевые решения лишь тогда, когда определитель матрицы равен нулю, получим уравнение для определения собственных значений det(A – λ E) = 0, (3.36) которое называется характеристическим или вековым уравнением. Если раскрыть определитель, то получим в левой части (3.36) многочлен n -й степени, корнями которого являются собственные значения матрицы A. На практике, при больших порядках n матрицы, задача раскрытия определителя (3.36) является сложной. Как известно из алгебры, многочлен n -й степени имеет n корней (действительных или комплексных), если кратные корни учитывать столько раз, какова их кратность. Пример 3.9. Найти собственные значения и собственные векторы матрицы
Решение. Составим характеристическое уравнение и решим его:
Найдем собственные векторы, решая системы уравнений.
Отсюда следует, что x 3 — произвольное число. Выберем x 3 = 1, тогда
Первое и второе уравнения оказались одинаковыми, мы получили одно уравнение с двумя неизвестными. Пусть x 2 = 1, тогда x 1 = –0,618 и второй собственный вектор равен x 2 = (–0,618; 1; 0) T.
Аналогично предыдущему, пусть x 1 = 1, тогда x 2 = 0,618 и третий собственный вектор равен x 3 = (1; 0,618; 0) T. Нормируем найденные векторы, т.е. разделим каждый вектор на его длину:
Правильность вычислений можно проверить в программе Mathcad с помощью функций eigenvals(A) и eigenvecs(A):
Как видим, результаты ручного расчета практически совпадают со значениями, полученными в программе Mathcad. Проверьте самостоятельно, что найденные собственные векторы взаимно ортогональны, т.е. при i ≠ k равно нулю скалярное произведение Вычислить собственные значения матрицы в общем случае труднее, чем найти при известных собственных значениях соответствующие собственные векторы. В некоторых частных случаях собственные значения вычисляются легко. Например, если матрица диагональная или треугольная, то определитель равен произведению диагональных элементов и поэтому собственные значения равны диагональным элементам. Нетрудно вычислить собственные значения для трехдиагональной матрицы, а также для почти треугольной матрицы. Для диагональной матрицы собственному значению λ i = aii отвечает единичный собственный вектор x i = (0, …, 1, …,0) T, у которого i -я компонента равна 1, а остальные компоненты равны 0. Теорема 3.5. Собственные значения симметричной матрицы с действительными элементами действительны, а собственные векторы, соответствующие различным собственным значениям, взаимно ортогональны. Теорема 3.6. Если λmin и λmax — наименьшее и наибольшее собственные значения действительной симметричной матрицы A, то для любого вектора x справедливо неравенство
λmin(x, x) ≤ (A x, x) ≤ λmax(x, x) (3.37)
Определение 3.6. Действительная симметричная матрица A называется положительно определенной, если для любого вектора x ≠ 0 выполняется условие (A x, x) > 0 (3.38) Теорема 3.7. Действительная симметричная матрица A является положительно определенной тогда и только тогда, когда все её собственные значения положительны. Теорема 3.8 (критерий Сильвестра). Для того чтобы действительная симметричная матрица A = [ aij ] была положительно определенной необходимо и достаточно, чтобы все главные диагональные миноры её определителя были положительны:
Теорема 3.9 (теорема Перрона). Если все элементы квадратной матрицы положительны, то её наибольшее по модулю собственное значение положительно и не является кратным, а соответствующий собственный вектор имеет положительные координаты. Рассмотрим итерационный метод определения наибольшего по модулю собственного значения и соответствующего собственного вектора матрицы A, который запишем в виде следующего алгоритма [7]:
|

 .
.




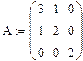
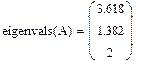

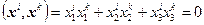 .
.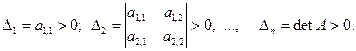 (3.39)
(3.39)


