Теорема Ляпунова.Теперь вычислим период, для этого составим дифференциальные уравнения, которым удовлетворяют переменные ρ и θ. Вычислим
Заменяя в системе (1.15) производные
Из второго уравнения определим t:
Для того чтобы удовлетворить условиям (1.13), необходимо константу (1.17) принять равной нулю. Используем тот факт, что ρ - аналитическая функция μ. Это позволит разложить подынтегральную функцию в выражении (1.17) в ряд по степеням μ
где
не зависит от θ0 и его можно записать в виде
где
не зависящие от θ0. Пусть теперь Ф(θ) – некоторая периодическая функция θ периода 2π, тогда
Рассматривая ее как функцию t, будем иметь
Равенство (1.19) справедливо для любых θ, следовательно, и равенство (1.20) справедливо для любых t, т. е. Ф(t) – периодическая функция t. Значит, величина Т, определенная формулой (1.18) как функция μ, и есть период решения. Используя (1.17), мы можем записать его в следующем виде:
где Покажем теперь, что Т- четная функция μ. Вернемся сова к интегралу (1.11). рассматривая его как уравнение относительно ρ, мы получаем в окрестности точки ρ=0 два решения. Одно из них
другое
Теперь заметим, что левая часть уравнения (1.11) не изменится, если заменим ρ на -ρ и θ на θ + 2π. Следовательно, на основании (1.21) будем иметь
Значение ρ, определенное рядом (1.22), будет корнем уравнения (1.11), не совпадающее с (1.21) (потому, что для малых ρ из (1.21) следует ρ = μ+О(μ2), а из (1.22) ρ = - μ+О(μ2)). Следовательно, оно будет определяться рядом (1.21’). Сравнивая (1.21’) и (1.22), получаем
и т.д. Отсюда следует, что если в выражении (1.21) заменить μ на – μ, а θ на θ + π, то величина ρ примет свое значение с обратным знаком:
Выпишем теперь выражение для периода Т. На основании (1.17) имеем
Сделаем замену в (1.23) замену μ на –μ, а θ на θ + π. Тогда получим величину
Согласно доказанному величины
Итак,
т. е. период – четная функция величины μ. Таким образом, выше было доказано теорему Ляпунова, а теперь сформулируем ее. Теорема Ляпунова. Если постоянная достаточно мала, то все решения системы уравнения (1.8) ─ периодические функции t, причем период ─ четная функция величин и при стремится к. Решения системы (1.8) являются аналитическими функциями величины c ─ начального отклонения переменной x. Имея в виду формулу выражение периода можно переписать в следующем виде:
Раздел 2. Условия существования периодических решений
|

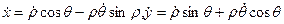 (1.15)
(1.15)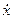 и
и 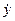 их выражениями из уравнений (1.8) и разрешая полученную систему относительно производных
их выражениями из уравнений (1.8) и разрешая полученную систему относительно производных 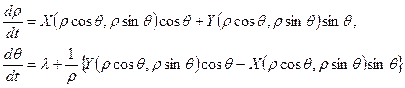 (1.16)
(1.16)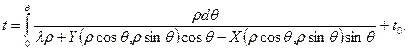 (1.17)
(1.17)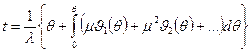 (1.17’)
(1.17’)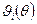 - периодические функции θ периода 2π. Следовательно, подынтегральная функция в (1.17’) также периодическаяфункцияθ периода 2π. Следовательно, интеграл
- периодические функции θ периода 2π. Следовательно, подынтегральная функция в (1.17’) также периодическаяфункцияθ периода 2π. Следовательно, интеграл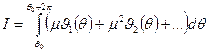
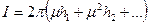 ,
,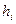 - вполне определенные числа. Таким образом, при измени θ; на 2π время t получает приращение Т
- вполне определенные числа. Таким образом, при измени θ; на 2π время t получает приращение Т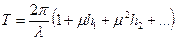 , (1.18)
, (1.18)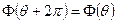 . (1.19)
. (1.19)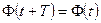 . (1.20)
. (1.20)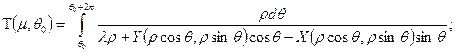
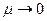 период Т стремится к периоду линейных колебаний 2π/λ, т. е. к периоду колебаний в системе (1.8) при
период Т стремится к периоду линейных колебаний 2π/λ, т. е. к периоду колебаний в системе (1.8) при 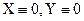 .
.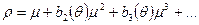 (1.21)
(1.21)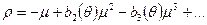 (1.21’)
(1.21’)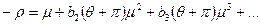 (1.22)
(1.22)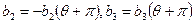
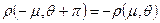 .
.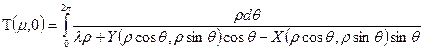 . (1.23)
. (1.23)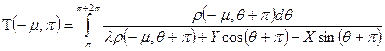 .
.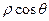 и
и 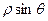 сохраняют свои значения. Следовательно, то же самое можно сказать и о функциях Х и Y. В то же время
сохраняют свои значения. Следовательно, то же самое можно сказать и о функциях Х и Y. В то же время 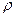 ,
, 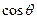 и
и 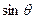 изменяют свои знаки. Следовательно, знаменатель изменит знак на обратный, но и числитель изменит знак на обратный. Следовательно,
изменяют свои знаки. Следовательно, знаменатель изменит знак на обратный, но и числитель изменит знак на обратный. Следовательно,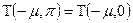 .
.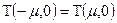 ,
,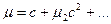
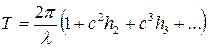 (1.24)
(1.24)


