Определение наибольших ошибок переноса Числовые значения характеристик ПН изменяются в зависимости от количества наблюдаемых машин N и условий их эксплуатации. Оценивают эти изменения доверительными границами или доверительным интервалом.
При расчетах характеристик ПН и переносе их на другие группы машин той же марки необходимо оценивать наибольшую возможную ошибку такого переноса. Абсолютная ошибка переноса опытных характеристик ПН при заданной доверительной вероятности будет равна величин e α .
Для удобства расчета относительную предельную ошибку δ определяют в процентах от среднего значения ПН
Например, при расчете среднего доремонтного ресурса двигателя для N =69 и α=0,90 относительную ошибку переноса может достигать предельной величины:
ПРИЛОЖЕНИЕ
Таблица 1. Варианты контрольного задания
№
НАРОБОТКА НА ОТКАЗ, МОТО-ЧАС
с
Таблица 1. Интегральная функция закона нормального распределения
0,50 0,51 0,52 0,53 0,54 0,55 0,56 0,57 0,58 0,59 0,60 0,61 0,62 0,63 0,64 0,65 0,66 0,67
0,000 0,025 0,051 0,075 0,100 0,125 0,150 0,176 0,202 0,228 0,254 0,279 0,306 0,332 0,358 0,385 0,412 0,440
0,68 0,69 0,70 0,71 0,72 0,73 0,74 0,75 0,76 0,77 0,78 0,79 0,80 0,81 0,82 0,83 0,84 0,85
0,468 0,469 0,524 0,553 0,583 0,613 0,643 0,674 0,706 0,739 0,772 0,806 0,842 0,878 0,915 0,954 0,995 1,036
0,86 0,87 0,88 0,89 0,90 0,91 0,92 0,93 0,94 0,95 0,96 0,97 0,98 0,99 0,999 0,9999 0,99999
1,080 1,126 1,175 1,227 1,281 1,341 1,405 1,476 1,555 1,645 1,751 1,881 2,054 2,326 3,090 3,720 4,265
Таблица 2. Коэффициенты Ирвина
Повторность информации N
Повторность информации N
2,8
2,2
1,5
1,3
3,7
2,9
2,0
1,8
1,2
1,1
1,0
0,9
1,7
1,6
1,5
1,3
Таблица 3. Дифференциальная функция (функция плотности вероятности) закона нормального распределения (ЗНР)
Сотые доли
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,8
3,0
0,40
0,40
0,39
0,38
0,37
0,35
0,33
0,31
0,29
0,27
0,24
0,22
0,19
0,17
0,15
0,13
0,11
0,09
0,08
0,07
0,05
0,04
0,04
0,03
0,02
0,02
0,01
0,01
0,00
0,40
0,40
0,39
0,38
0,37
0,35
0,33
0,31
0,29
0,26
0,24
0,22
0,19
0,17
0,15
0,13
0,11
0,09
0,08
0,06
0,05
0,04
0,04
0,03
0,02
0,02
0,01
0,01
0,00
0,40
0,40
0,39
0,38
0,37
0,35
0,33
0,31
0,29
0,26
0,24
0,21
0,19
0,17
0,15
0,13
0,11
0,09
0,08
0,06
0,05
0,04
0,03
0,03
0,02
0,02
0,01
0,01
0,00
0,40
0,40
0,39
0,38
0,37
0,35
0,33
0,31
0,29
0,26
0,24
0,21
0,19
0,17
0,15
0,13
0,11
0,09
0,08
0,06
0,05
0,04
0,03
0,03
0,02
0,02
0,01
0,01
0,00
0,40
0,40
0,39
0,38
0,36
0,35
0,33
0,30
0,28
0,26
0,23
0,21
0,19
0,16
0,14
0,12
0,10
0,09
0,08
0,06
0,05
0,04
0,03
0,03
0,02
0,02
0,01
0,01
0,00
0,40
0,40
0,39
0,38
0,36
0,34
0,32
0,30
0,28
0,25
0,23
0,21
0,18
0,16
0,14
0,12
0,10
0,09
0,07
0,06
0,05
0,04
0,03
0,03
0,02
0,02
0,01
0,01
0,00
0,40
0,39
0,39
0,37
0,36
0,34
0,32
0,30
0,28
0,25
0,23
0,20
0,18
0,16
0,14
0,12
0,10
0,09
0,07
0,06
0,05
0,04
0,03
0,03
0,02
0,02
0,01
0,01
0,00
0,40
0,39
0,39
0,37
0,36
0,34
0,32
0,30
0,27
0,25
0,23
0,20
0,18
0,16
0,14
0,12
0,10
0,08
0,07
0,06
0,05
0,04
0,03
0,02
0,02
0,02
0,01
0,01
0,00
0,40
0,39
0,38
0,37
0,36
0,34
0,32
0,29
0,27
0,25
0,22
0,20
0,18
0,15
0,13
0,12
0,10
0,08
0,07
0,06
0,05
0,04
0,03
0,02
0,02
0,01
0,01
0,01
0,00
0,40
0,39
0,38
0,37
0,35
0,34
0,31
0,29
0,27
0,24
0,22
0,20
0,17
0,15
0,13
0,11
0,10
0,08
0,07
0,06
0,05
0,04
0,03
0,02
0,02
0,01
0,01
0,01
0,00
Таблица 4. Параметры и коэффициенты закона распределения Вейбулла (ЗРВ)
b
V
0,800
0,820
0,840
0,860
0,880
0,900
0,920
0,940
0,960
0,980
0,000
1,040
1,080
1,120
1,160
1,200
1,240
1,280
1,320
1,360
1,400
1,420
1,440
1,460
1,480
1,500
1,520
1,540
1,560
1,580
1,600
1,620
1,640
1,660
1,680
1,700
1,720
1,740
1,760
1,780
1,800
1,820
1,840
1,860
1,880
1,900
1,920
1,940
1,960
1,980
2,000
2,020
2,040
2,060
2,080
2,100
2,120
2,140
2,160
2,180
2,200
2,220
2,240
2,260
2,280
2,300
2,320
2,340
2,360
2,380
2,400
2,420
2,440
2,460
2,480
2,500
2,520
2,540
2,560
2,580
2,600
2,620
2,640
2,680
2,700
2,720
2,740
2,760
2,780
2,800
2,820
2,840
2,860
2,880
2,900
2,920
2,940
2,960
2,980
3,000
3,020
3,040
3,060
3,080
3,100
3,120
3,140
3,160
3,180
3,200
3,220
3,240
3,260
3,280
3,300
3,320
3,340
3,360
3,380
3,400
3,420
3,440
3,460
3,480
3,500
3,520
3,540
3,560
3,580
3,600
3,620
3,640
3,660
3,680
3,700
3,720
3,740
3,760
3,780
3,800
3,820
3,840
3,860
3,880
3,900
3,920
3,940
3,960
3,980
4,000
4,020
4,040
4,060
4,080
4,100
4,120
4,140
4,160
4,180
4,200
1,133
1,114
1,096
1,080
1,066
1,052
1,040
1,029
1,018
1,009
1,000
0,984
0,971
0,959
0,949
0,941
0,933
0,926
0,921
0,916
0,911
0,909
0,908
0,906
0,904
0,903
0,901
0,900
0,899
0,898
0,897
0,896
0,895
0,894
0,893
0,892
0,892
0,891
0,890
0,890
0,889
0,889
0,888
0,888
0,888
0,887
0,887
0,887
0,887
0,886
0,886
0,886
0,886
0,886
0,886
0,886
0,886
0,886
0,886
0,886
0,886
0,886
0,886
0,886
0,886
0,886
0,886
0,886
0,886
0,886
0,886
0,887
0,887
0,887
0,887
0,887
0,887
0,888
0,888
0,888
0,888
0,888
0,889
0,889
0,889
0,889
0,890
0,890
0,890
0,890
0,891
0,891
0,891
0,891
0,892
0,892
0,892
0,892
0,893
0,893
0,893
0,893
0,894
0,894
0,894
0,895
0,895
0,895
0,895
0,896
0,896
0,896
0,896
0,897
0,897
0,897
0,898
0,898
0,898
0,898
0,899
0,899
0,899
0,899
0,900
0,900
0,900
0,901
0,901
0,901
0,901
0,902
0,902
0,902
0,902
0,903
0,903
0,903
0,903
0,904
0,904
0,904
0,905
0,905
0,905
0,905
0,906
0,906
0,906
0,906
0,907
0,907
0,907
0,907
0,908
0,908
0,908
0,908
0,909
0,909
1,428
1,367
1,311
1.261
1,214
1,171
1,132
1,095
1,061
1,029
1,000
0,947
0,900
0,858
0,821
0,787
0,757
0,729
0,704
0,681
0,660
0,650
0,640
0,631
0,622
0,613
0,605
0,579
0,589
0,581
0,574
0,567
0,560
0,553
0,546
0,540
0,534
0,528
0,522
0,517
0,511
0,506
0,501
0,496
0,491
0,486
0,481
0,476
0,472
0,468
0,463
0,459
0,455
0,451
0,447
0,443
0,439
0,436
0,432
0,428
0,425
0,421
0,418
0,415
0,412
0,408
0,405
0,402
0,399
0,396
0,393
0,391
0,388
0,385
0,382
0,380
0,377
0,374
0,372
0,369
0,367
0,364
0,362
0,357
0,355
0,353
0,351
0,348
0,346
0,344
0,342
0,340
0,338
0,336
0,334
0,332
0,330
0,328
0,326
0,325
0,323
0,321
0,319
0,317
0,316
0,314
0,312
0,310
0,309
0,307
0,306
0,304
0,302
0,301
0,299
0,298
0,296
0,295
0,293
0,292
0,290
0,289
0,287
0,286
0,285
0,283
0,282
0,281
0,279
0,278
0,277
0,275
0,274
0,273
0,272
0,270
0,269
0,268
0,267
0,266
0,264
0,263
0,262
0,261
0,260
0,259
0,258
0,256
0,255
0,254
0,253
0,252
0,251
0,250
0,246
0,248
0,247
0,246
0,245
0,244
1,261
1,227
1,196
1,167
1,139
1,113
1,088
1,064
1,042
1,020
1,000
0,962
0,927
0,894
0,865
0,837
0,811
0,787
0,765
0,744
0,724
0,714
0,705
0,696
0,687
0,679
0,671
0,663
0,655
0,647
0,640
0,633
0,626
0,619
0,612
0,605
0,599
0,593
0,587
0,581
0,575
0,569
0,564
0,558
0,553
0,547
0,542
0,537
0,532
0,527
0,523
0,518
0,513
0,509
0,505
0,500
0,496
0,492
0,488
0,484
0,480
0,476
0,472
0,468
0,465
0,461
0,457
0,454
0,451
0,447
0,444
0,441
0,437
0,434
0,431
0,428
0,425
0,422
0,419
0,416
0,413
0,410
0,407
0,402
0,399
0,397
0,394
0,392
0,389
0,387
0,384
0,382
0,379
0,377
0,375
0,372
0,370
0,368
0,366
0,363
0,361
0,359
0,357
0,355
0,353
0,351
0,349
0,347
0,345
0,343
0,341
0,339
0,337
0,335
0,334
0,332
0,330
0,328
0,326
0,325
0,323
0,321
0,320
0,318
0,316
0,315
0,313
0,312
0,310
0,308
0,307
0,305
0,304
0,302
0,301
0,299
0,298
0,297
0,295
0,294
0,292
0,291
0,290
0,288
0,287
0,286
0,284
0,283
0,282
0,280
0,279
0,278
0,277
0,276
0,274
0,273
0,272
0,271
0,270
0,268
2,815
2,707
2,608
2,514
2,427
2,345
2,268
2,195
2,127
2,062
2,000
1,886
1,782
1,688
1,601
1,521
1,447
1,378
1,314
1,255
1,198
1,172
1,146
1,120
1,096
1,072
1,049
1,026
1,004
0,983
0,962
0,942
0,922
0,902
0,883
0,865
0,847
0,829
0,812
0,795
0,779
0,763
0,747
0,731
0,716
0,701
0,687
0,672
0,658
0,645
0,631
0,618
0,605
0,592
0,579
0,567
0,555
0,543
0,531
0,520
0,509
0,498
0,487
0,476
0,465
0,455
0,444
0,434
0,424
0,415
0,405
0,395
0,386
0,377
0,368
0,359
0,350
0,341
0,332
0,324
0,315
0,307
0,299
0,283
0,275
0,267
0,260
0,252
0,245
0,237
0,230
0,223
0,216
0,209
0,202
0,195
0,188
0,181
0,175
0,168
0,162
0,155
0,149
0,143
0,136
0,130
0,124
0,118
0,112
0,106
0,101
0,095
0,089
0,983
0,078
0,072
0,067
0,061
0,056
0,051
0,046
0,040
0,035
0,030
0,025
0,020
0,015
0,010
0,005
0,001
–0,004
–0,009
–0,014
–0,018
–0,023
–0,027
–0,032
–0,036
–0,041
–0,045
–0,050
–0,054
–0,058
–0,062
–0,067
–0,071
–0,075
–0,079
–0,083
–0,087
–0,091
–0,095
–0,099
–0,103
–0,107
–0,111
–0,115
–0,118
–0,122
0,126
0,669
0,661
0,658
0,655
0,652
0,649
0,645
0,641
0,638
0,635
0,632
0,626
0,620
0,615
0,610
0,605
0,600
0,596
0,592
0,588
0,584
0,582
0,580
0,578
0,577
0,576
0,574
0,572
0,570
0,569
0,568
0,566
0,564
0,563
0,562
0,561
0,559
0,558
0,557
0,556
0,555
0,553
0,552
0,551
0,550
0,549
0,548
0,547
0,546
0,545
0,544
0,543
0,542
0,541
0,540
0,539
0,538
0,537
0,536
0,535
0,535
0,534
0,533
0,533
0,532
0,531
0,531
0,530
0,529
0,528
0,527
0,527
0,526
0,526
0,525
0,524
0,524
0,523
0,522
0,521
0,520
0,520
0,519
0,518
0,517
0,517
0,516
0,516
0,515
0,514
0,514
0,513
0,513
0,512
0,512
0,511
0,511
0,510
0,510
0,509
0,509
0,508
0,508
0,507
0,507
0,507
0,506
0,506
0,505
0,505
0,505
0,504
0,504
0,503
0,503
0,503
0,502
0,502
0,501
0,501
0,501
0,500
0,500
0,499
0,499
0,499
0,498
0,498
0,497
0,497
0,497
0,496
0,496
0,495
0,495
0,495
0,495
0,494
0,494
0,494
0,494
0,494
0,493
0,493
0,493
0,492
0,492
0,492
0,491
0,491
0,491
0,490
0,490
0,489
0,489
0,489
0,488
0,488
0,487
0,487
Таблица 5. Дифференциальная функция (функция плотности вероятности) законараспределения Вейбулла (ЗРВ)
Параметр b
1,0
1,2
1,4
1,6
1,8
2,0
3,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
0,91
0,82
0,74
0,67
0,61
0,55
0,50
0,45
0,41
0,37
0,33
0,30
0,27
0,25
0,22
0,20
0,18
0,17
0,15
0,14
0,12
0,11
0,10
0,09
0,08
0,71
0,75
0,75
0,72
0,68
0,63
0,58
0,53
0,49
0,44
0,40
0,36
0,32
0,29
0,26
0,23
0,20
0,18
0,16
0,14
0,12
0,11
0,09
0,08
0,07
0,54
0,66
0,72
0,74
0,73
0,70
0,55
0,62
0,57
0,52
0,46
0,41
0,37
0,32
0,28
0,25
0,21
0,18
0,16
0,13
0,11
0,09
0,08
0,07
0,06
0,39
0,57
0,67
0,73
0,76
0,76
0,73
0,70
0,65
0,59
0,53
0,47
0,41
0,35
0,30
0,25
0,21
0,18
0,14
0,12
0,09
0,08
0,06
0,05
0,04
0,28
0,47
0,61
0,71
0,78
0,80
0,80
0,77
0,72
0,66
0,59
0,52
0,45
0,38
0,31
0,26
0,21
0,16
0,13
0,10
0,07
0,05
0,04
0,03
0,02
0,20
0,38
0,55
0,68
0,78
0,84
0,86
0,84
0,80
0,74
0,66
0,57
0,48
0,39
0,32
0,25
0,19
0,14
0,10
0,07
0,05
0,04
0,02
0,02
0,01
0,03
0,12
0,26
0,45
0,66
0,87
1,04
1,15
1,17
1,10
0,96
0,77
0,56
0,38
0,23
0,13
0,06
0,03
0,01
0,00
0,00
–
–
–
–
Таблица 6. Вероятность совпадения
1 2 3 4 5 6 7 8 9 10
0,00 0,10 0,35 0,71 1,14 1,64 2,17 2,73 3,32 3,94
0,02 0,21 0,58 1,06 1,61 2,20 2,83 3,49 4,17 4,86
0,06 0,45 1,00 1,65 2,34 3,07 3,82 4,59 5,38 6,18
0,15 0,71 1,42 2,20 3,00 3,83 4,67 5,53 6,39 7,27
0,45 1,39 2,37 3,36 4,35 5,35 6,34 7,34 8,34 9,34
1,07 2,41 3,66 4,88 6,06 7,23 8,38 9,52 10,7 11,8
1,64 3,22 4,64 5,99 7,29 8,56 9,80 11,0 12,2 13,4
2,71 4,60 6,25 7,78 9,24 10,6 12,0 13,4 14,7 16,0
Таблица 7. Коэффициенты
N
α=0,60
α =0,80
α =0,90
α =0,95
1,06
0,98
0,94
0,92
0,91
0,90
0,89
0,88
0,88
0,88
0,87
0,87
0,87
0,86
0,86
0,85
0,85
0,85
0,85
0,85
0,85
1,95
1,74
1,62
1,54
1,48
1,43
1,40
1,37
1,34
1,33
1,31
1,29
1,28
1,24
1,21
1,18
1,16
1,14
1,12
1,10
1,09
0,70
0,73
0,75
0,76
0,77
0,78
0,79
0,80
0,80
0,81
0,81
0,83
0,83
0,85
0,86
0,87
0,88
0,89
0,90
0,91
0,92
1,89
1,64
1,53
1,48
1,44
1,42
1,40
1,38
1,37
1,36
1,36
1,35
1,35
1,33
1,32
1,31
1,30
1,30
1,30
1,29
1,29
2,73
2,29
2,05
1,90
1,80
1,72
1,66
1,61
1,57
1,53
1,50
1,48
1,46
1,37
1,33
1,29
1,24
1,21
1,19
1,16
1,14
0,57
0,60
0,62
0,65
0,67
0,68
0,69
0,70
0,70
0,71
0,73
0,74
0,74
0,77
0,79
0,70
0,73
0,84
0,86
0,87
0,88
2,92
2,35
2,13
2,02
1,94
1,90
1,86
1,83
1,81
1,80
1,78
1,77
1,76
1,73
1,71
1,70
1,68
1,68
1,67
1,66
1,66
3,66
2,93
2,54
2,29
2,13
2,01
1,91
1,83
1,78
1,73
1,69
1,65
1,62
1,51
1,44
1,39
1,32
1,28
1,25
1,21
1,19
0,48
0,52
0,55
0,57
0,59
0,61
0,63
0,64
0,64
0,65
0,66
0,67
0,68
0,72
0,74
0,76
0,78
0,80
0,82
0,84
0,86
4,30
3,18
3,78
2,57
2,45
2,37
2,31
2,26
2,23
2,20
2,18
2,16
2,15
2,09
2,06
2,04
2,02
2,01
2,00
1,99
1,98
4,85
3,67
3,07
2,72
2,48
2,32
2,18
2,09
2,00
1,94
1,88
1,83
1,79
1,64
1,55
1,48
1,40
1,35
1,31
1,27
1,23
0,42
0,46
0,49
0,51
0,54
0,56
0,57
0,59
0,60
0,61
0,62
0,63
0,64
0,67
0,70
0,72
0,75
0,77
0,79
0,81
0,83
Таблица 9. Интегральная функция (функция распределения)
Параметр b
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
0,12
0,21
0,29
0,35
0,41
0,47
0,52
0,56
0,60
0,63
0,66
0,69
0,72
0,74
0,76
0,78
0,80
0,82
0,83
0,85
0,86
0,87
0,88
0,89
0,90
0,91
0,91
0,92
0,10
0,18
0,26
0,33
0,39
0,45
0,50
0,55
0,59
0,63
0,67
0,70
0,73
0,75
0,78
0,80
0,82
0,84
0,85
0,87
0,88
0,89
0,90
0,91
0,92
0,93
0,93
0,94
0,08
0,16
0,23
0,31
0,37
0,43
0,49
0,54
0,59
0,63
0,67
0,71
0,74
0,77
0,79
0,81
0,83
0,85
0,87
0,88
0,90
0,91
0,92
0,93
0,94
0,94
0,95
0,96
0,06
0,12
0,19
0,26
0,33
0,40
0,47
0,53
0,58
0,63
0,67
0,71
0,75
0,78
0,80
0,83
0,85
0,87
0,89
0,90
0,91
0,92
0,93
0,94
0,95
0,96
0,96
0,97
0,05
0,12
0,19
0,26
0,33
0,40
0,47
0,53
0,58
0,63
0,68
0,72
0,76
0,79
0,82
0,84
0,86
0,88
0,90
0,92
0,93
0,94
0,95
0,96
0,96
0,97
0,97
0,98
0,04
0,10
0,17
0,24
0,32
0,39
0,46
0,52
0,58
0,63
0,68
0,73
0,76
0,80
0,83
0,86
0,88
0,90
0,91
0,93
0,94
0,95
0,96
0,97
0,97
0,98
0,98
0,99
0,03
0,
Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
Дизартрии у детей Выделение клинических форм дизартрии у детей является в большой степени условным, так как у них крайне редко бывают локальные поражения мозга, с которыми связаны четко определенные синдромы двигательных нарушений...
Педагогическая структура процесса социализации Характеризуя социализацию как педагогический процессе, следует рассмотреть ее основные компоненты: цель, содержание, средства, функции субъекта и объекта...
Типовые ситуационные задачи. Задача 1. Больной К., 38 лет, шахтер по профессии, во время планового медицинского осмотра предъявил жалобы на появление одышки при значительной физической
Задача 1. Больной К., 38 лет, шахтер по профессии, во время планового медицинского осмотра предъявил жалобы на появление одышки при значительной физической нагрузке. Из медицинской книжки установлено, что он страдает врожденным пороком сердца....
Тактика действий нарядов полиции по предупреждению и пресечению правонарушений при проведении массовых мероприятий К особенностям проведения массовых мероприятий и факторам, влияющим на охрану общественного порядка и обеспечение общественной безопасности, можно отнести значительное количество субъектов, принимающих участие в их подготовке и проведении...
Тактические действия нарядов полиции по предупреждению и пресечению групповых нарушений общественного порядка и массовых беспорядков В целях предупреждения разрастания групповых нарушений общественного порядка (далееГНОП) в массовые беспорядки подразделения (наряды) полиции осуществляют следующие мероприятия...
Механизм действия гормонов а) Цитозольный механизм действия гормонов. По цитозольному механизму действуют гормоны 1 группы...
, независимо от выбранного закона распределения:
(32)
%.
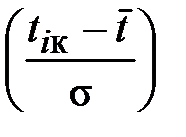
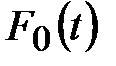
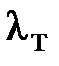
при α=0,95
при
α =0,99
при
α =0,95
при
α =0,99
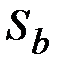
% по критерию согласия 
и 
для двусторонних доверительных границ
закона распределения Вейбулла (ЗРВ)
