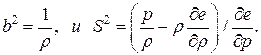Переход к недивергентным формам записи системы уравнений Навье-СтоксаПри использовании дивергентной формы записи (уравнение (8)) искомый вектор состояния течения находится в массовых переменных, как комбинация газодинамических параметров. Это не всегда удобно. Для нахождения самих параметров течения переходят к другим формам представления исходной системы.При этом, как правило, теряется дивергентность, но для гладких решений точность вычислений не ухудшается. Рассмотрим новый вектор состояния потока (см.[7]):
Рассмотрим более подробно производную от вектора потока. Сам вектор потока равен
Например, если Теперь полученное выражение для производной вектора потока подставим в уравнение (13):
и после преобразований получаем квазилинейное уравнение второго порядка Здесь Последняя система уравнений уже недивергентного вида. Рассмотрим три частных случая этой системы уравнений в зависимости от нового вектора состояния течения 1. В случае, когда новый вектор потока равен
систему уравнений, для нахождения которой: 1) сначала находим матрицу Якоби и матрицу, обратную к ней
тогда
2) дальше надо находить производные от вектора потока
3) Для нахождения матрицы В недивергентной формы записи системы имеем:
Аналогично находится матрица С= Таким образом, в одномерном случае уравнение (14) с вектором течения Для нахождения коэффициентов системы уравнений недивергентной формы рассмотрим и другой способ решения. Он сводится к преобразованию уже полученной ранее дивергентной системы (11) с учетом нового вектора течения
Учитывая уравнение состояния
Выписывая теперь матрицу коэффициентов системы (16) при первых частных производных вектора течения
Матрица совпадает с вычисленной раньше матрицей В. Из системы (16) также можно выписать и другие коэффициенты:
В многомерном случае, когда новый вектор состояния течения равен
Здесь коэффициенты
где
2. Рассмотрим другой случай, когда новый вектор течения ищется в переменных:
3. В третьем случае, когда новый вектор течения
|


 , взаимообратный к вектору
, взаимообратный к вектору  . Перейдем в уравнении (8) к вектору
. Перейдем в уравнении (8) к вектору  по формуле:
по формуле:  . Здесь матрица
. Здесь матрица  есть матрица Якоби, обратная к которой
есть матрица Якоби, обратная к которой  . Умножим уравнение (8) на матрицу
. Умножим уравнение (8) на матрицу  . Получим новую недивергентную форму представления системы уравнений
. Получим новую недивергентную форму представления системы уравнений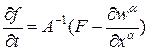 . (13)
. (13) . Тогда
. Тогда .
. , то
, то  , тогда
, тогда  .
.
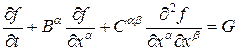 (14)
(14) .
. .
. система уравнений
система уравнений с искомым вектором
с искомым вектором  преобразуется в
преобразуется в
 ,
, (см.уравнение (11)):
(см.уравнение (11)):  и
и  И после вычислений получаем:
И после вычислений получаем:
 .
. и вектор правых частей
и вектор правых частей 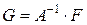 .
. получается следующее
получается следующее  Здесь
Здесь  , а матрица В вычислена раньше.
, а матрица В вычислена раньше. . Выпишем систему (11):
. Выпишем систему (11): (15)
(15) , можно заменить производную давления во втором уравнении системы (15) по формуле
, можно заменить производную давления во втором уравнении системы (15) по формуле  . Тогда система преобразуется в следующую:
. Тогда система преобразуется в следующую: (16)
(16) , получаем
, получаем .
. .
. , аналогично одномерному случаю, получаем первый матричный коэффициент недивергентной формы записи системы (14):
, аналогично одномерному случаю, получаем первый матричный коэффициент недивергентной формы записи системы (14): .
. и
и 
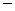 символы Кронекера. Другие коэффициенты недивергентной системы равны:
символы Кронекера. Другие коэффициенты недивергентной системы равны: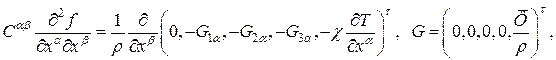


 ,
,  . В этом случае меняются коэффициенты
. В этом случае меняются коэффициенты  и
и  . Из уравнений состояния
. Из уравнений состояния  и
и  находим
находим  ,
, . Заменяя градиент давления во втором уравнении системы (16), получаем:
. Заменяя градиент давления во втором уравнении системы (16), получаем:  . В уравнении энергии заменяем производные
. В уравнении энергии заменяем производные  и, используя уравнение неразрывности преобразуем его к виду:
и, используя уравнение неразрывности преобразуем его к виду: . Тогда для нового вектора течения матрица
. Тогда для нового вектора течения матрица . Здесь
. Здесь  .
. ,
,  , после преобразований получаем матрицу
, после преобразований получаем матрицу Здесь
Здесь