Исходные данные
Анализируется одноконтурная замкнутая импульсная САУ, состоящая из непрерывной части (НЧ) и импульсного элемента (ИЭ), формирующего прямоугольные импульсы длительностью  , где T – период дискретизации,
, где T – период дискретизации, 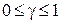 . Исходные данные для расчетов приведены в таблице 4. Для всех вариантов заданий передаточная функция непрерывной части имеет вид
. Исходные данные для расчетов приведены в таблице 4. Для всех вариантов заданий передаточная функция непрерывной части имеет вид
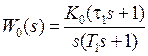 .
.
Импульсный элемент представляется в виде идеального ключа и формирующего устройства с передаточной функцией
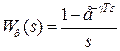 .
.
Структурная схема системы представлена на рисунке 3. В таблице 4
T – период дискретизации; T 1, 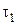 – постоянные времени имеют размерность секунды; К 0 – коэффициент передачи НЧ имеет размерность с-1 и выбирается далее.
– постоянные времени имеют размерность секунды; К 0 – коэффициент передачи НЧ имеет размерность с-1 и выбирается далее.

Рисунок 3
Таблица 4
| Номер варианта
| 
| Т
| Т 1
| 
|
|
| 0, 3
|
|
| 0, 1
|
|
| 0, 3
| 0, 9
| 0, 9
| 0, 2
|
|
| 0, 3
| 0, 8
| 0, 8
| 0, 2
|
|
| 0, 3
| 0, 7
| 0, 7
| 0, 1
|
|
| 0, 3
| 0, 6
| 0, 6
| 0, 1
|
|
| 0, 3
| 0, 5
| 0, 5
| 0, 2
|
|
| 0, 3
| 0, 4
| 0, 4
| 0, 2
|
|
| 0, 3
| 0, 3
| 0, 3
| 0, 1
|
|
| 0, 3
| 0, 2
| 0, 2
| 0, 1
|
|
| 0, 3
| 0, 1
| 0, 1
| 0, 05
|
|
| 0, 5
|
|
|
|
|
| 0, 5
| 0, 9
| 0, 9
|
|
|
| 0, 5
| 0, 8
| 0, 8
|
|
|
| 0, 7
| 0, 7
| 0, 7
|
|
|
| 0, 7
| 0, 6
| 0, 6
|
|
|
| 0, 7
| 0, 5
| 0, 5
|
|
|
| 0, 7
| 0, 4
| 0, 4
|
|
|
| 0, 8
| 0, 3
| 0, 3
|
|
|
| 0, 8
| 0, 2
| 0, 2
|
|
|
| 0, 8
| 0, 1
| 0, 1
|
|
|
|
|
|
|
|
|
|
| 0, 9
| 0, 9
|
|
|
|
| 0, 8
| 0, 8
|
|
|
|
| 0, 7
| 0, 7
|
|
|
|
| 0, 6
| 0, 6
|
|
|
|
| 0, 5
| 0, 5
| 0, 1
|
|
|
| 0, 4
| 0, 4
| 0, 1
|
|
|
| 0, 3
| 0, 3
| 0, 1
|
|
|
| 0, 2
| 0, 2
| 0, 01
|
|
|
| 0, 1
| 0, 1
| 0, 01
|
Задание
1. Найти передаточные функции импульсной САУ:  – разомкнутой системы,
– разомкнутой системы,  – замкнутой системы,
– замкнутой системы,  – системы по ошибке. Параметры T, T 1,
– системы по ошибке. Параметры T, T 1, 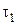 , K 0,
, K 0, 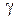 входят в выражения передаточных функций в общем виде, т.е. в буквенном виде. Далее в пункте 3.2 знак * будет относиться к передаточным функциям импульсной системы.
входят в выражения передаточных функций в общем виде, т.е. в буквенном виде. Далее в пункте 3.2 знак * будет относиться к передаточным функциям импульсной системы.
2. Найти интервал изменения коэффициента передачи K 0, при котором система будет устойчива 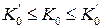 . Для дальнейших исследований выбрать значение
. Для дальнейших исследований выбрать значение 
3. Построить графики логарифмических частотных характеристик разомкнутой импульсной системы  и
и 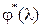 при заданных значениях T, T 1,
при заданных значениях T, T 1, 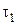 ,
, 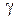 и выбранном
и выбранном  . По графикам определить запасы устойчивости системы по модулю
. По графикам определить запасы устойчивости системы по модулю  и фазе
и фазе  .
.
4. Определить ошибку системы по скорости 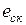 при входном воздействии
при входном воздействии 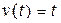 (скачок по скорости), а также первые два коэффициента ошибок
(скачок по скорости), а также первые два коэффициента ошибок  .
.
5. Вычислить переходной процесс в системе при воздействии  (скачок по положению).
(скачок по положению).
Краткие методические указания
1. Основное для дальнейшего правильно определить передаточную функцию разомкнутой системы. Приведем краткую методику, следуя
[5, с. 24-31], [6, с. 412]. Передаточную функцию 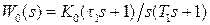 представляем в виде суммы двух слагаемых
представляем в виде суммы двух слагаемых  , где A и B выражаются через
, где A и B выражаются через 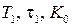 . Далее к
. Далее к 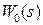 применяется Z -преобразование и получается передаточная функция импульсной системы
применяется Z -преобразование и получается передаточная функция импульсной системы 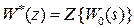 .
.
В соответствии с [5, с. 31] имеем  ,
, 
 ,
,  .
.
Таким образом, имеем
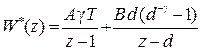 ,
,
где в коэффициенты A, B входит коэффициент передачи K 0. Полученную
передаточную функцию в конечном виде можно представить следующим образом
 .
.
Передаточные функции замкнутой системы легко находятся по
выражениям
 ,
, 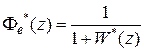 .
.
2. Устойчивость системы определяется корнями характеристического уравнения замкнутой системы 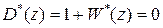 , которое для нашего случая будет иметь вид
, которое для нашего случая будет иметь вид 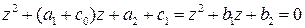 . В соответствии с алгебраическим критерием [6, c. 432] замкнутая система будет устойчива при выполнении неравенств
. В соответствии с алгебраическим критерием [6, c. 432] замкнутая система будет устойчива при выполнении неравенств
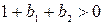 ,
, 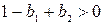 ,
, 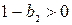 .
.
В неравенстве при известных значениях 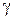 ,
, 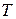 ,
,  ,
, 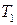 входит величина K 0.
входит величина K 0.
Таким образом, можно выделить отрезок значений 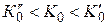 , при которых система будет устойчива и далее принять
, при которых система будет устойчива и далее принять 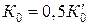 .
.
3. Для построения логарифмических характеристик разомкнутой системы в передаточной функции  делаем замену переменной [5, с. 40],
делаем замену переменной [5, с. 40],
[6, с. 433]
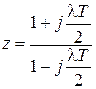 ,
,  ,
,
где 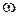 - обычная частота,
- обычная частота,  - псевдочастота,
- псевдочастота,  мнимая единица. При изменении частоты
мнимая единица. При изменении частоты 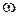 в диапазоне
в диапазоне 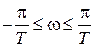 псевдочастота изменяется от
псевдочастота изменяется от 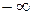 до
до 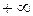 , при
, при  псевдочастота
псевдочастота 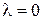 . В результате замены передаточная функция
. В результате замены передаточная функция 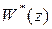 преобразуется в частотную характеристику относительно псевдочатоты следующего вида
преобразуется в частотную характеристику относительно псевдочатоты следующего вида
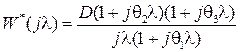 ,
,
где  - некоторые числа при заданных K 0,
- некоторые числа при заданных K 0, 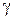 ,
, 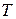 ,
,  ,
, 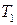 . Величины
. Величины  можно интерпретировать как постоянные времени, причем некоторые из них могут быть отрицательными. Далее находится
можно интерпретировать как постоянные времени, причем некоторые из них могут быть отрицательными. Далее находится 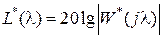 ,
, 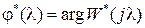 - амплитудная и фазовая частотные логарифмические характеристики системы. Построение их производится как и для непрерывного случая (смотри примеры [5, c. 41-43, 6, c. 434]).
- амплитудная и фазовая частотные логарифмические характеристики системы. Построение их производится как и для непрерывного случая (смотри примеры [5, c. 41-43, 6, c. 434]).
По построенным характеристикам 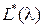 и
и 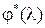 определяем частоту среза
определяем частоту среза  там, где
там, где 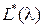 пересекает ось абсцисс
пересекает ось абсцисс  , а также точку, где
, а также точку, где  . В этих точках находим запасы устойчивости системы по модулю
. В этих точках находим запасы устойчивости системы по модулю  и фазе
и фазе  .
.
Следует помнить, что исходя из пункта 2 при заданных параметрах, система всегда будет устойчива.
4. Рассматриваемая система для всех вариантов является астатической с астатизмом первого порядка и имеет следующую передаточную функцию

где  .
.
В силу астатизма первого порядка в такой системе статическая ошибка всегда равна нулю, а скоростная  вычисляется по формуле
вычисляется по формуле 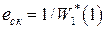 . Величина
. Величина  , а коэффициент ошибки
, а коэффициент ошибки  находится по следующей
находится по следующей
формуле
 ,
,
где 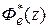 - передаточная функция системы по ошибке. Более подробно смотри [11, c. 115].
- передаточная функция системы по ошибке. Более подробно смотри [11, c. 115].
5. В случае низкого порядка системы переходной процесс на выходе в дискретные моменты времени 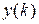 нетрудно вычислить аналитически, либо путем моделирования в среде Matlab (в последнем случае ограничения на порядок системы не имеет значения).
нетрудно вычислить аналитически, либо путем моделирования в среде Matlab (в последнем случае ограничения на порядок системы не имеет значения).
Рассмотрим два способа аналитического вычисления процесса 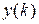 .
.
Первый способ базируется на дискретном преобразовании Лапласа
(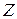 -преобразовании). В этом случае [11, с. 43] реакция системы на единичное воздействие – переходная функция, которая вычисляется по формуле
-преобразовании). В этом случае [11, с. 43] реакция системы на единичное воздействие – переходная функция, которая вычисляется по формуле
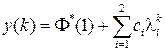 ,
,
где 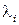 два различных корня характеристического уравнения замкнутой системы
два различных корня характеристического уравнения замкнутой системы  ,
,  - передаточная функция замкнутой системы, а
- передаточная функция замкнутой системы, а  вычисляются из выражения
вычисляются из выражения
 ,
,  .
.
Задавая  , получим значения
, получим значения  и построим точечный график переходного процесса. Если корни уравнения
и построим точечный график переходного процесса. Если корни уравнения  одинаковые (кратный корень), то существует аналогичная формула [11] вычисления
одинаковые (кратный корень), то существует аналогичная формула [11] вычисления  .
.
Второй вариант [6, c. 411] вычисления переходного процесса базируется на рекуррентных свойствах разностных уравнений. Если известна передаточная функция замкнутой системы
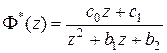 ,
,
то несложно найти разностное уравнение, связывающее выход  и вход
и вход 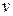 в дискретные моменты времени k
в дискретные моменты времени k
 ,
,
которые можно представить в виде
 .
.
Зададим начальные значения переменных  ,
,  ,
,  , тогда с учетом
, тогда с учетом  получаем рекуррентное соотношение для вычисления
получаем рекуррентное соотношение для вычисления  . Задавая последовательно
. Задавая последовательно  ,
,  ,
,  и т. д. находим
и т. д. находим 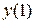 ,
,  и т.д. Зная
и т.д. Зная  ,
, 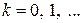 можно построить точечный график переходного процесса.
можно построить точечный график переходного процесса.

 , где T – период дискретизации,
, где T – период дискретизации, 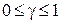 . Исходные данные для расчетов приведены в таблице 4. Для всех вариантов заданий передаточная функция непрерывной части имеет вид
. Исходные данные для расчетов приведены в таблице 4. Для всех вариантов заданий передаточная функция непрерывной части имеет вид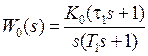 .
.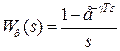 .
.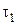 – постоянные времени имеют размерность секунды; К 0 – коэффициент передачи НЧ имеет размерность с-1 и выбирается далее.
– постоянные времени имеют размерность секунды; К 0 – коэффициент передачи НЧ имеет размерность с-1 и выбирается далее.


 – разомкнутой системы,
– разомкнутой системы,  – замкнутой системы,
– замкнутой системы,  – системы по ошибке. Параметры T, T 1,
– системы по ошибке. Параметры T, T 1, 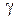 входят в выражения передаточных функций в общем виде, т.е. в буквенном виде. Далее в пункте 3.2 знак * будет относиться к передаточным функциям импульсной системы.
входят в выражения передаточных функций в общем виде, т.е. в буквенном виде. Далее в пункте 3.2 знак * будет относиться к передаточным функциям импульсной системы.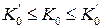 . Для дальнейших исследований выбрать значение
. Для дальнейших исследований выбрать значение 
 и
и 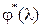 при заданных значениях T, T 1,
при заданных значениях T, T 1,  . По графикам определить запасы устойчивости системы по модулю
. По графикам определить запасы устойчивости системы по модулю  и фазе
и фазе  .
.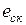 при входном воздействии
при входном воздействии 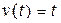 (скачок по скорости), а также первые два коэффициента ошибок
(скачок по скорости), а также первые два коэффициента ошибок  .
. (скачок по положению).
(скачок по положению).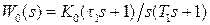 представляем в виде суммы двух слагаемых
представляем в виде суммы двух слагаемых  , где A и B выражаются через
, где A и B выражаются через 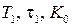 . Далее к
. Далее к 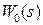 применяется Z -преобразование и получается передаточная функция импульсной системы
применяется Z -преобразование и получается передаточная функция импульсной системы 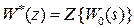 .
.  ,
, 
 ,
,  .
.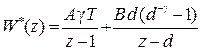 ,
, .
. ,
, 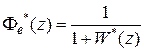 .
.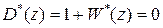 , которое для нашего случая будет иметь вид
, которое для нашего случая будет иметь вид 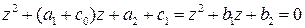 . В соответствии с алгебраическим критерием [6, c. 432] замкнутая система будет устойчива при выполнении неравенств
. В соответствии с алгебраическим критерием [6, c. 432] замкнутая система будет устойчива при выполнении неравенств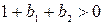 ,
, 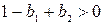 ,
, 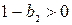 .
.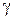 ,
, 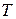 ,
,  ,
, 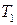 входит величина K 0.
входит величина K 0.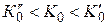 , при которых система будет устойчива и далее принять
, при которых система будет устойчива и далее принять 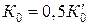 .
. делаем замену переменной [5, с. 40],
делаем замену переменной [5, с. 40], 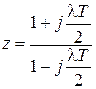 ,
,  ,
,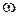 - обычная частота,
- обычная частота,  - псевдочастота,
- псевдочастота,  мнимая единица. При изменении частоты
мнимая единица. При изменении частоты 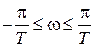 псевдочастота изменяется от
псевдочастота изменяется от 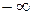 до
до 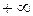 , при
, при  псевдочастота
псевдочастота 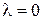 . В результате замены передаточная функция
. В результате замены передаточная функция 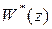 преобразуется в частотную характеристику относительно псевдочатоты следующего вида
преобразуется в частотную характеристику относительно псевдочатоты следующего вида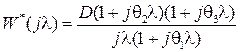 ,
, - некоторые числа при заданных K 0,
- некоторые числа при заданных K 0, 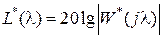 ,
, 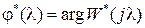 - амплитудная и фазовая частотные логарифмические характеристики системы. Построение их производится как и для непрерывного случая (смотри примеры [5, c. 41-43, 6, c. 434]).
- амплитудная и фазовая частотные логарифмические характеристики системы. Построение их производится как и для непрерывного случая (смотри примеры [5, c. 41-43, 6, c. 434]).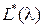 и
и 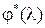 определяем частоту среза
определяем частоту среза  там, где
там, где  . В этих точках находим запасы устойчивости системы по модулю
. В этих точках находим запасы устойчивости системы по модулю 
 .
. вычисляется по формуле
вычисляется по формуле 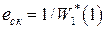 . Величина
. Величина  , а коэффициент ошибки
, а коэффициент ошибки  находится по следующей
находится по следующей  ,
,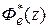 - передаточная функция системы по ошибке. Более подробно смотри [11, c. 115].
- передаточная функция системы по ошибке. Более подробно смотри [11, c. 115].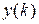 нетрудно вычислить аналитически, либо путем моделирования в среде Matlab (в последнем случае ограничения на порядок системы не имеет значения).
нетрудно вычислить аналитически, либо путем моделирования в среде Matlab (в последнем случае ограничения на порядок системы не имеет значения).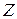 -преобразовании). В этом случае [11, с. 43] реакция системы на единичное воздействие – переходная функция, которая вычисляется по формуле
-преобразовании). В этом случае [11, с. 43] реакция системы на единичное воздействие – переходная функция, которая вычисляется по формуле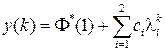 ,
,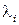 два различных корня характеристического уравнения замкнутой системы
два различных корня характеристического уравнения замкнутой системы  ,
,  - передаточная функция замкнутой системы, а
- передаточная функция замкнутой системы, а  вычисляются из выражения
вычисляются из выражения ,
,  .
. , получим значения
, получим значения  и построим точечный график переходного процесса. Если корни уравнения
и построим точечный график переходного процесса. Если корни уравнения  одинаковые (кратный корень), то существует аналогичная формула [11] вычисления
одинаковые (кратный корень), то существует аналогичная формула [11] вычисления 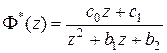 ,
, и вход
и вход 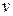 в дискретные моменты времени k
в дискретные моменты времени k ,
, .
. ,
,  ,
,  , тогда с учетом
, тогда с учетом  получаем рекуррентное соотношение для вычисления
получаем рекуррентное соотношение для вычисления  ,
,  ,
,  и т. д. находим
и т. д. находим 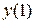 ,
,  и т.д. Зная
и т.д. Зная 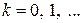 можно построить точечный график переходного процесса.
можно построить точечный график переходного процесса.


