Проекция точки на выпуклые множестваРасстояние d от точки v до множества Х в евклидовом пространстве определяется по формуле d = inf ê ê v - х ê ê;. xÎ Х Определение 3.3. Точка р Î xÎ Х Теорема 3.5. Для любого множества Х ¹ Æ и любой точки v существует точка рÎ Доказательство. Если vÎ X, то p = v, d =0. Пусть vÎ X. Так как X¹ Æ, то существует точка у Î Х. Рассмотрим множество: Y={x/x Î Х, //v-x//£ //v-y//}. (3.4) Очевидно, что расстояние от v до х совпадает с расстоянием от v до Y и проекция точки v на X совпадает с проекциейточки v на Y (если эта проекция существует). Найдем проекцию v на Y. В силу определения нижней грани существует последовательность {xk}Ì Y, такая что lim // v - xk // = d (3.5)
Из ограниченности Y следует ограниченность последовательности {xk}, поэтому из неё можно выделить последовательность {xki} такую что lim xki = p, (3.6)
где pÎ Окончательно получаем также, что // v - p // = d, т.е. p есть проекция точки v. Теорема 3.6. Для того, чтобы точка рÎ < (x-p), (v-p)> £ 0. (3.7) По определению скалярного произведения
< (x-p), (v- p)> = ||x -p|| × || v-p|| cos((x-p), (v-p)), (3.8) то есть знак скалярного произведения определяется углом между векторами (x-p) и (v-p). Таким образом (см. рисунок 3.4) точка pÎ
x X Рис. 3. 4.
Доказательство 1.Необходимость. Пусть р проекция точки v на Х. Если vÎ Рассмотрим случай, когда vÏ z(a)= (1-a)p + a x, где aÎ [0, 1] (3.9) Так как р – проекция, то 0 £ ||x - z(a)||2 + || v-p||2=-2a < (x-p), (v-p)> + a2|| x-p||2 (3.10) для всех aÎ [0, 1]. Это неравенство возможно при всех aÎ [0, 1] лишь в том случае, если выполняется неравенство (3.7). 2. Достаточность. Пусть (3.7) справедливо для любого хÎ || v-x||2 = ||(v -p)+(p-x)||2 =|| v-p||2 + 2 < (v-p), (p -x)> + || p -x||2³ || v-p||2 т.е. p есть проекция v на X Следствие 3.2. Проекция любой точки vÎ Еn на выпуклое множество Х единственна. Доказательство. Если vÎ || v-p||2 = ||(v –p’)+(p’-p)||2 =|| v-p||2 + 2 < (v-p’), (p-p)> +|| p’-p||2. Откуда следует что || v-p||2> ||(v –p’)||. Полученное противоречие доказывает теорему. Следует сделать замечание, что для множества, не являющегося выпуклым, следствие может не выполняться (см. рис. 3.5)
Х р2
Рис. 3. 5
|

 называется проекцией точки v на множество Х, если ê ê v - р ê ê = inf ê ê v - х ê ê;.
называется проекцией точки v на множество Х, если ê ê v - р ê ê = inf ê ê v - х ê ê;. , являющаяся проекцией точки v.
, являющаяся проекцией точки v. k ¥
k ¥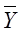 Ì
Ì 
 v
v
 p
p р1
р1 
 v
v


