Множество всех собственных векторов, соответствующих данному собственному значению линейного оператора, не является линейным подпространством, так как это множество не содержит нулевого вектора, который, по определению, не может быть собственным.
Обозначим через 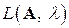 множество всех собственных векторов линейного оператора
множество всех собственных векторов линейного оператора 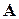 , соответствующих собственному значению
, соответствующих собственному значению 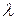 , с добавленным к этому множеству нулевым вектором
, с добавленным к этому множеству нулевым вектором 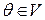 :
:
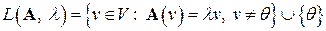 .
.
Теорема 5.13. Множество 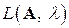 является линейным подпространством пространства
является линейным подпространством пространства 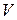 .
.
□ Покажем, что множество 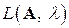 замкнуто относительно операций сложения векторов и умножения вектора на число, то есть при всех
замкнуто относительно операций сложения векторов и умножения вектора на число, то есть при всех  и
и 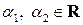 :
: 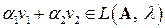 .
.
Действительно, имеем
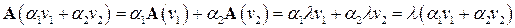 ,
,
что и означает, что вектор 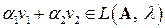 . ■
. ■
Определение 5.13. Подпространство 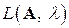 называется собственным подпространством линейного оператора
называется собственным подпространством линейного оператора 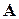 .
.
Определение 5.14. Геометрической кратностью  собственного значения
собственного значения 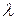 линейного оператора
линейного оператора 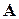 называется размерность собственного подпространства
называется размерность собственного подпространства 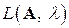 :
: 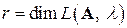 .
.
Согласно определению 5.14, геометрическая кратность собственного значения равна числу  линейно независимых собственных векторов
линейно независимых собственных векторов 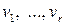 , соответствующих этому собственному значению. Например, для линейного оператора из примера 5.2 были получены два собственных значения
, соответствующих этому собственному значению. Например, для линейного оператора из примера 5.2 были получены два собственных значения  . При этом геометрические кратности для каждого из них равны соответственно
. При этом геометрические кратности для каждого из них равны соответственно
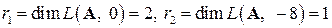 .
.
Теорема 5.14. Если 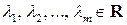 – попарно различные собственные значения линейного оператора
– попарно различные собственные значения линейного оператора 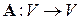 , то система
, то система

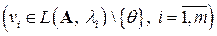
соответствующих им собственных векторов линейно независима.
□ Доказательство проведем методом математической индукции по числу 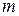 векторов.
векторов.
При 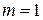 (база индукции) утверждение теоремы верно, так как линейная независимость системы из одного вектора
(база индукции) утверждение теоремы верно, так как линейная независимость системы из одного вектора 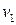 означает, что этот вектор ненулевой, а вектор
означает, что этот вектор ненулевой, а вектор  является ненулевым, так как он собственный вектор для оператора
является ненулевым, так как он собственный вектор для оператора 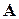 .
.
Предположим, что утверждение теоремы верно при 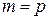 , то есть если
, то есть если 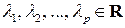 попарно различные собственные значения линейного оператора
попарно различные собственные значения линейного оператора 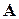 , то система
, то система

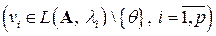
соответствующих им собственных векторов линейно независима (предположение индукции).
Покажем, что утверждение теоремы верно для 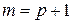 (шаг индукции), то есть система векторов
(шаг индукции), то есть система векторов

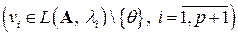 (5.8)
(5.8)
линейно независима (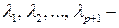 попарно различные собственные значения линейного оператора
попарно различные собственные значения линейного оператора 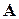 ).
).
Запишем линейную комбинацию векторов (5.8) с произвольными весовыми коэффициентами 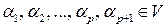 и приравняем ее нулевому вектору
и приравняем ее нулевому вектору
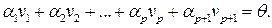 (5.9)
(5.9)
Найдем образы векторов в левой и правой частей равенства (5.9). Учитывая линейность оператора 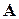 , а также равенства
, а также равенства  , получим
, получим
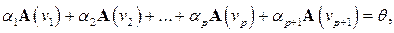
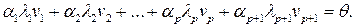 (5.10)
(5.10)
Умножив равенство (5.10) на число 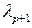 , получим
, получим
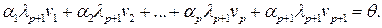
Вычтем последнее равенство из равенства (5.10):
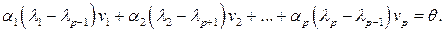
В силу того, что система векторов 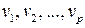 линейно независима, получим, что в последнем равенстве все весовые коэффициенты равны нулю:
линейно независима, получим, что в последнем равенстве все весовые коэффициенты равны нулю:
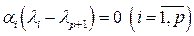 .
.
Так как все собственные значения 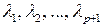 попарно различны, то
попарно различны, то
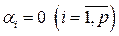 .
.
При этом равенство (5.9) примет вид
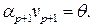
Так как собственный вектор 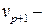 ненулевой, то
ненулевой, то  Итак, в равенстве (5.9) все весовые коэффициенты равны нулю:
Итак, в равенстве (5.9) все весовые коэффициенты равны нулю: 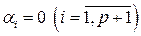 , что и означает линейную независимость системы векторов (5.8). ■
, что и означает линейную независимость системы векторов (5.8). ■
Теорема 5.15. Два собственных подпространства  и
и 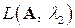 , соответствующие двум различным собственным значениям
, соответствующие двум различным собственным значениям  (
(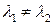 ) линейного оператора
) линейного оператора 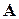 , пересекаются по нулевому вектору.
, пересекаются по нулевому вектору.
□ Предположим, что 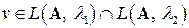 . Покажем, что
. Покажем, что  . Так как
. Так как 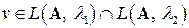 , то
, то  . Вычитая из первого равенства второе равенство, получим
. Вычитая из первого равенства второе равенство, получим
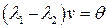 .
.
Так как по условию теоремы 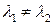 , то последнее равенство возможно только в том случае, когда
, то последнее равенство возможно только в том случае, когда  . ■
. ■
[1] Это подпространство называется алгебраическим дополнением к подпространству ядра оператора

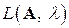 множество всех собственных векторов линейного оператора
множество всех собственных векторов линейного оператора 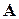 , соответствующих собственному значению
, соответствующих собственному значению 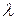 , с добавленным к этому множеству нулевым вектором
, с добавленным к этому множеству нулевым вектором 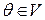 :
: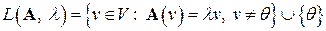 .
.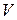 .
. и
и 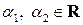 :
: 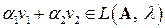 .
.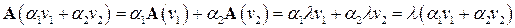 ,
, собственного значения
собственного значения 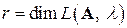 .
.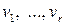 , соответствующих этому собственному значению. Например, для линейного оператора из примера 5.2 были получены два собственных значения
, соответствующих этому собственному значению. Например, для линейного оператора из примера 5.2 были получены два собственных значения  . При этом геометрические кратности для каждого из них равны соответственно
. При этом геометрические кратности для каждого из них равны соответственно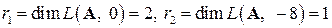 .
.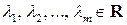 – попарно различные собственные значения линейного оператора
– попарно различные собственные значения линейного оператора 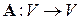 , то система
, то система
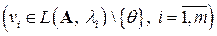
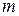 векторов.
векторов.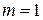 (база индукции) утверждение теоремы верно, так как линейная независимость системы из одного вектора
(база индукции) утверждение теоремы верно, так как линейная независимость системы из одного вектора 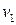 означает, что этот вектор ненулевой, а вектор
означает, что этот вектор ненулевой, а вектор  является ненулевым, так как он собственный вектор для оператора
является ненулевым, так как он собственный вектор для оператора 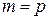 , то есть если
, то есть если 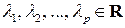 попарно различные собственные значения линейного оператора
попарно различные собственные значения линейного оператора 
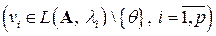
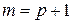 (шаг индукции), то есть система векторов
(шаг индукции), то есть система векторов
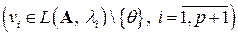 (5.8)
(5.8)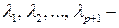 попарно различные собственные значения линейного оператора
попарно различные собственные значения линейного оператора 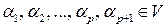 и приравняем ее нулевому вектору
и приравняем ее нулевому вектору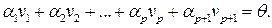 (5.9)
(5.9) , получим
, получим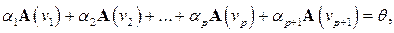
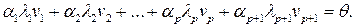 (5.10)
(5.10)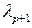 , получим
, получим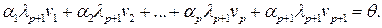
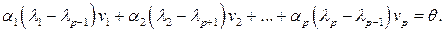
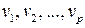 линейно независима, получим, что в последнем равенстве все весовые коэффициенты равны нулю:
линейно независима, получим, что в последнем равенстве все весовые коэффициенты равны нулю: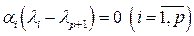 .
.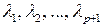 попарно различны, то
попарно различны, то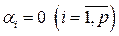 .
.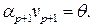
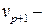 ненулевой, то
ненулевой, то  Итак, в равенстве (5.9) все весовые коэффициенты равны нулю:
Итак, в равенстве (5.9) все весовые коэффициенты равны нулю: 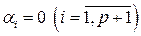 , что и означает линейную независимость системы векторов (5.8). ■
, что и означает линейную независимость системы векторов (5.8). ■ и
и 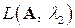 , соответствующие двум различным собственным значениям
, соответствующие двум различным собственным значениям  (
(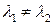 ) линейного оператора
) линейного оператора 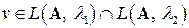 . Покажем, что
. Покажем, что  . Так как
. Так как  . Вычитая из первого равенства второе равенство, получим
. Вычитая из первого равенства второе равенство, получим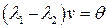 .
.


