Числовые характеристики дискретных случайных величинОпределение. Математическим ожиданием (средним значением) M X дискретной случайной величины X называют сумму произведений значений xi случайной величины и вероятностей pi = P{ Х = xi }, с которыми случайная величина принимает эти значения:
т.е. ряд, определяющий математическое ожидание, сходится абсолютно; в противном случае говорят, что математическое ожидание случайной величины X не существует. Определение. Дисперсией D Х случайной величины X называют математическое ожидание квадрата отклонения случайной величины X от ее среднего значения, т.е.
Дисперсия дискретной случайной величины вычисляется по формуле
Нетрудно видеть, что дисперсия D X имеет размерность квадрата размерности случайной величины X. Для практических же целей удобно иметь величину, характеризующую разброс значений случайной величины вокруг ее математического ожидания, размерность которой совпадает с размерностью X. В качестве такой величины естественно использовать
Пример 1. Математическое ожидание и дисперсию случайной величины X, распределенной по биномиальному закону (число успехов в n испытаниях по схеме Бернулли с вероятностью успеха р):
Пример 2. Пусть случайная величина X имеет распределение Пуассона. Тогда
Пример 3. Пусть случайная величина X имеет геометрическое распределение:
Определение. Функцией распределения (вероятностей) случайной величины X называют функцию F (x), значение которой в точке х равно вероятности события { X < x }, т.е. события, состоящего из тех и только тех элементарных исходов ω, для которых F (x) = P{ X < x } Обычно говорят, что значение функции распределения в точке х равно вероятности того, что случайная величина X примет значение, меньшее х. Теорема. Функция распределения обладает следующими свойствами: 1) 2) F (x 1) < F (x 2) при x 1 < x 2 (т.е. F (x) − неубывающая функция); 3) 4) 5) F (x) = F (x − 0), где
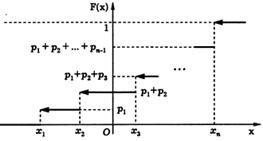
Покажем теперь, как по ряду распределения дискретной случайной величины построить ее функцию распределения F (x). Пусть X − дискретная случайная величина, заданная своим рядом распределения, причем значения x 1, x 2,..., хn расположены в порядке возрастания. Тогда для всех х ≤ x 1 событие { X < x } является невозможным и поэтому в соответствии с определением F (x) = 0. Если x 1 < х ≤ х 2, то событие { X < х }состоит из тех и только тех элементарных исходов ω,для которых Х (ω) = x 1, и, следовательно, F (x) = p. Аналогично при x 2 < х ≤ х 3 событие { X < х } состоит из элементарных исходов ω, для которых либо Х (ω) = х 1, либо Х (ω) = х 2, т.е. { X < x } = { X = x 1} + { X = x 2},а следовательно, F (x) = p 1 + p 2 и т.д. Наконец, при х > хn событие { X < х } достоверно и F (х) = 1. Таким образом, функция распределения дискретной случайной величины является кусочно постоянной функцией, принимающей на промежутке (−∞, x 1] значение 0, на промежутках (xi, xi + 1], 1 ≤ i < n, − значение p 1 +... + pi и на промежутке (хn, +∞) − значение 1.
|

 . При этом, если множество возможных значений случайной величины X счетно, предполагается, что
. При этом, если множество возможных значений случайной величины X счетно, предполагается, что


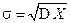 , которую называют средним квадратичным отклонением случайной величины X (иногда также стандартом, или стандартным отклонением).
, которую называют средним квадратичным отклонением случайной величины X (иногда также стандартом, или стандартным отклонением).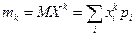 Определение. k -тым центральным моментом дискретной случайной величины X называют математическое ожидание от k -той степени центрированной случайной величины:
Определение. k -тым центральным моментом дискретной случайной величины X называют математическое ожидание от k -той степени центрированной случайной величины:
 Момент первого порядка совпадает с математическим ожиданием, центральный момент первого порядка равен нулю, центральный момент второго порядка является дисперсией. Отметим также, что в теоретических изысканиях рассматривают моменты не обязательно целого порядка k.
Мода случайной величины дискретного типа определяется как такое возможное значение хт, для которого
Момент первого порядка совпадает с математическим ожиданием, центральный момент первого порядка равен нулю, центральный момент второго порядка является дисперсией. Отметим также, что в теоретических изысканиях рассматривают моменты не обязательно целого порядка k.
Мода случайной величины дискретного типа определяется как такое возможное значение хт, для которого
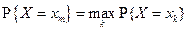 Таким образом, мода случайной величины дискретного типа есть ее наиболее вероятное значение в случае, если такое значение единственно. Мода может не существовать, иметь единственное значение (унимодальное распределение)или иметь множество значений (мультимодальное распределение).
Таким образом, мода случайной величины дискретного типа есть ее наиболее вероятное значение в случае, если такое значение единственно. Мода может не существовать, иметь единственное значение (унимодальное распределение)или иметь множество значений (мультимодальное распределение).

 где Хi − число успехов в i -м испытании. Нетрудно видеть, что
где Хi − число успехов в i -м испытании. Нетрудно видеть, что
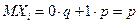 ,
, 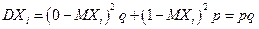 Значит, в силу свойства 3
Значит, в силу свойства 3 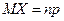 . Учитывая, что случайные величины Хi являются независимыми, в силу свойства 4 дисперсии получаем
. Учитывая, что случайные величины Хi являются независимыми, в силу свойства 4 дисперсии получаем 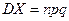 .
.
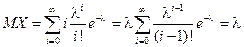
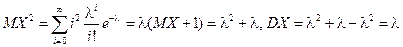
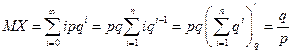
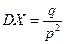
 :
: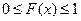 ;
;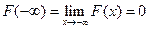 ,
,  ;
;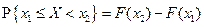 ;
;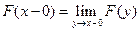 (т.е. F (x) − непрерывная слева функция).
(т.е. F (x) − непрерывная слева функция).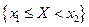 − случайная величина X приняла значение, лежащее в промежутке [ x 1, x 2). Поэтому в соответствии с аксиомой сложения получаем утверждение 4.
5) Наконец, пусть x 1,..., xn,... − любая возрастающая последовательность чисел, стремящаяся к х. Событие { X < х } является объединением событий { X < хn }. Снова воспользовавшись аксиомой непрерывности, приходим к утверждению 5.
− случайная величина X приняла значение, лежащее в промежутке [ x 1, x 2). Поэтому в соответствии с аксиомой сложения получаем утверждение 4.
5) Наконец, пусть x 1,..., xn,... − любая возрастающая последовательность чисел, стремящаяся к х. Событие { X < х } является объединением событий { X < хn }. Снова воспользовавшись аксиомой непрерывности, приходим к утверждению 5.