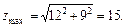Переменных
Введем новый тип экстремумов. Для этого рассмотрим целевую функцию
Геометрический смысл такой ситуации по казан на рис. 22.1, из которого ясно, что в этом случае можно рассматривать новый тип экстремальной задачи: найти точку (  ), лежащую на кривой j (x, y) = 0, в которой функция ), лежащую на кривой j (x, y) = 0, в которой функция 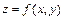 принимает максимальное (минимальное) значение. Такого рода экстремумы называют условными экстремумами. принимает максимальное (минимальное) значение. Такого рода экстремумы называют условными экстремумами.
Если уравнение j (x, y) = 0 разрешить относительно y, то поиск условного сведется к поиску обычного экстремума для функции Продифференцируем
Отсюда с помощью необходимого условия экстремума получаем
С другой стороны, х и у связаны функциональной зависимостью
Сравнивая производные (4.22.1) и (4.22.2), получаем равенство
равносильное системе двух уравнений
относительно неизвестных х, у, l. Введем так называемую функцию Лагранжа: F (x, y, l) =f (x, y) +lj (x, y). (4.22.4) Тогда необходимые условия экстремума для (4.22.4)
приводят нас к уравнениям (4.22.3) и условию j (х, у) = 0. Решая эти три уравнения, мы найдем точку условного экстремума. Таким образом, с помощью функции Лагранжа задача о поиске условного экстремума сводится к задаче о локальных экстремумах для функции Лагранжа. Для общего случая, когда z = f
функция Лагранжа строится по аналогии с (4.22.4):
П р и м е р Найти кратчайшее расстояние от начала координат до кривой Целевая функция здесь имеет вид
а затем записываем необходимые условия локального экстремума:
Используя первые два уравнения системы (4.22.5), находим
Подставляем это выражение в последнее уравнение системы (4.22.5)
Интерпретация полученных результатов ясна из рис. 4.22.2: в первой точке целевая функция достигает максимума, а во второй – минимума, причем
Достаточные условия условного экстремума используются очень редко и в нашем курсе не рассматриваются. Задание для самостоятельного решения 1. Найти экстремумы функции z = x 3при условии
2. Найти экстремумы функции z = xy при условии 2 х+ 3 у= 1.
|


 . Однако такая процедура часто бывает нерациональной или невозможной. Поэтому для поиска условных экстремумов был разработан специальный алгоритм – метод множителей Лагранжа, который мы сейчас рассмотрим.
. Однако такая процедура часто бывает нерациональной или невозможной. Поэтому для поиска условных экстремумов был разработан специальный алгоритм – метод множителей Лагранжа, который мы сейчас рассмотрим.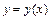 :
:
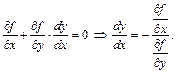 (4.22.1)
(4.22.1) , с помощью которой находим
, с помощью которой находим (4.22.2)
(4.22.2)
 (4.22.3)
(4.22.3)
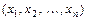 ,
,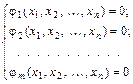

 .
. . Составляем функцию Лагранжа
. Составляем функцию Лагранжа ,
, (4.22.5)
(4.22.5)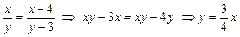 .
.
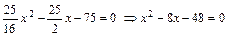


 ;
;