1) Интегрируя первый раз, получим  . После повторного интегрирования будем иметь
. После повторного интегрирования будем иметь
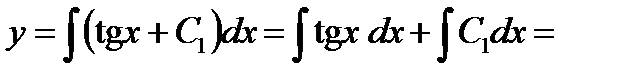

Следовательно,  - общее решение.
- общее решение.
2) Чтобы найти частное решение, подставим в полученное общее решение и в выражение для первой производной значения 
 и
и  , получим систему двух уравнений с неизвестными
, получим систему двух уравнений с неизвестными  и
и  :
:
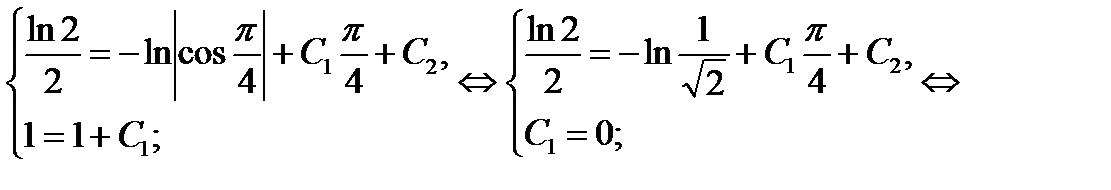
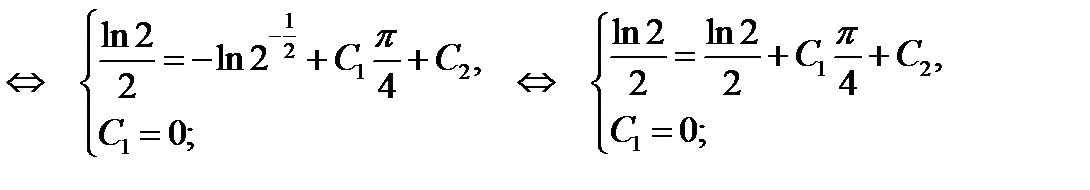
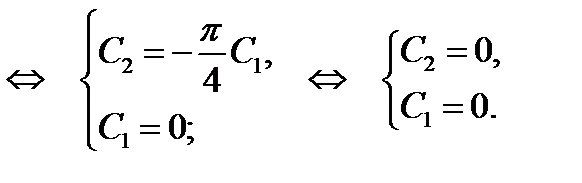
Подставив найденные  и
и  в общее решение получим искомое частное решение
в общее решение получим искомое частное решение  .
.
2.2.2 Уравнение вида
 . (2.7)
. (2.7)
Уравнение (2.7) не содержит искомой функции  и ее нескольких последовательных производных
и ее нескольких последовательных производных  (производных до (k-1) включительно). С помощью замены
(производных до (k-1) включительно). С помощью замены  понизим порядок уравнения на
понизим порядок уравнения на  единиц, тогда
единиц, тогда 
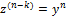
 . (2.8)
. (2.8)
Общее решение уравнения (2.8) имеет вид
 .
.
Тогда искомая функция  решение уравнения (2.7) получается с помощью
решение уравнения (2.7) получается с помощью  кратного интегрирования функции
кратного интегрирования функции 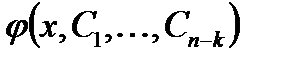 (см. п. 2.2.1).
(см. п. 2.2.1).
Для дифференциального уравнения второго порядка  не содержащего явно искомой функции y подстановка
не содержащего явно искомой функции y подстановка  , тогда
, тогда  преобразует данное уравнение в уравнение I порядка
преобразует данное уравнение в уравнение I порядка 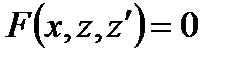
Пример Найти общее решение уравнения  .
.
Решение. Данное уравнение не содержит  и
и  . Положим
. Положим  , тогда
, тогда  и уравнение будет иметь вид:
и уравнение будет иметь вид:  . Это линейное уравнение первого порядка (см. п.1.4.). Его общее решение имеет вид
. Это линейное уравнение первого порядка (см. п.1.4.). Его общее решение имеет вид  . Так как
. Так как  , то для отыскания искомого общего решения надо проинтегрировать уравнение
, то для отыскания искомого общего решения надо проинтегрировать уравнение  . Таким образом,
. Таким образом,
 ,
,
тогда
 .
.
Следовательно,  , где
, где  - произвольные постоянные, является общим решением заданного уравнения.
- произвольные постоянные, является общим решением заданного уравнения.
2.2.3 Уравнения вида
 . (2.9)
. (2.9)
Уравнение (2.9) не содержит явно независимую переменную  . В этом случае примем
. В этом случае примем  за независимую переменную и введем новую функцию
за независимую переменную и введем новую функцию  . Считая, что
. Считая, что  есть функция от
есть функция от  и через посредство
и через посредство  зависит от
зависит от  и, применяя правило дифференцирования сложных функций, получим для производных от
и, применяя правило дифференцирования сложных функций, получим для производных от  по
по  выражения
выражения
 ,
,
 ,
,
аналогично вычисляются  .
.
Подставляя в уравнение (2.9) вместо  и т.д., увидим, что в новых переменных порядок уравнения будет
и т.д., увидим, что в новых переменных порядок уравнения будет  , т.е. на единицу ниже.
, т.е. на единицу ниже.
Если это преобразованное уравнение проинтегрировано и  - его решение, то нахождение общего интеграла данного уравнения сводится к интегрированию
- его решение, то нахождение общего интеграла данного уравнения сводится к интегрированию
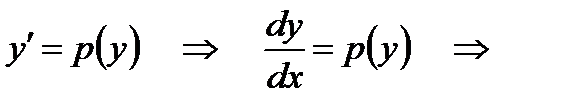
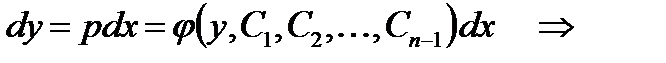
 .
.
Откуда получаем общее решение ОДУ (2.9)
 .
.
Одна из произвольных постоянных  входит в качестве слагаемого к
входит в качестве слагаемого к  , а это означает, что всякую интегральную кривую можно перемещать параллельно оси
, а это означает, что всякую интегральную кривую можно перемещать параллельно оси  .
.
Если дифференциальное уравнение не содержит независимой переменной x, искомой функции y(x) и ее производных до (k-1) порядка включительно, то порядок уравнения можно понизить на (k+1) применяя подстановку 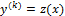

 , а затем
, а затем  .
.
Например, для дифференциального уравнения второго порядка, не содержащего независимой переменной x, т.е. уравнение имеет вид  подстановка
подстановка 
 сводит уравнение к уравнению первого порядка
сводит уравнение к уравнению первого порядка 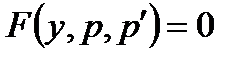
Пример Найти общий интеграл уравнения  .
.
Решение. Положим
 и подставим в исходное уравнение, тогда получим
и подставим в исходное уравнение, тогда получим
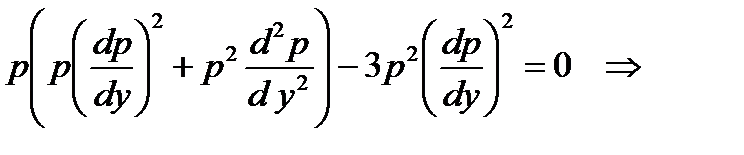
 .
.
Сократим на  , при этом учтем теряемое решение
, при этом учтем теряемое решение  или
или  и получим
и получим
 .
.
Это уравнение рассматриваемого вида, делая ту же замену  придем к уравнению
придем к уравнению
 .
.
Сократив на  (при этом учитываем еще одно решение
(при этом учитываем еще одно решение  , т.е.
, т.е.  и
и  ), получим
), получим
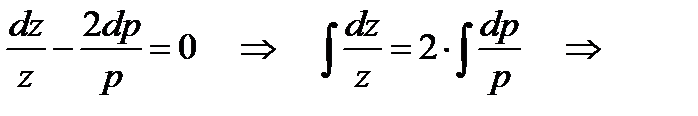
 .
.
Проинтегрировав уравнение  , находим
, находим  , или
, или  Окончательно получим
Окончательно получим
 , где
, где  .
.
Это семейство парабол. Заметим, что в общее решение входят и потерянные ранее частные решения (кроме  ).
).

 . После повторного интегрирования будем иметь
. После повторного интегрирования будем иметь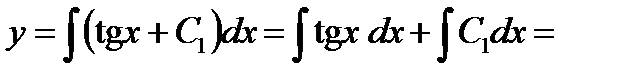

 - общее решение.
- общее решение.
 и
и  , получим систему двух уравнений с неизвестными
, получим систему двух уравнений с неизвестными  и
и  :
: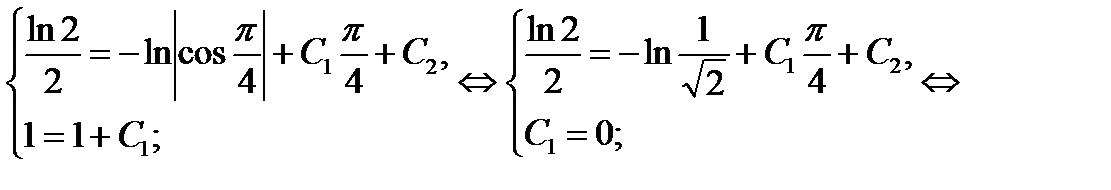
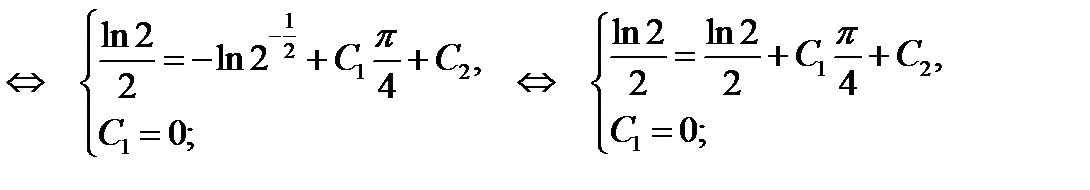
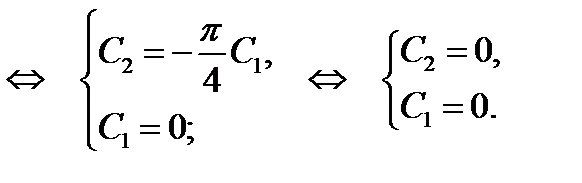
 и
и  в общее решение получим искомое частное решение
в общее решение получим искомое частное решение  .
. . (2.7)
. (2.7) и ее нескольких последовательных производных
и ее нескольких последовательных производных  (производных до (k-1) включительно). С помощью замены
(производных до (k-1) включительно). С помощью замены  понизим порядок уравнения на
понизим порядок уравнения на  единиц, тогда
единиц, тогда 
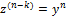
 . (2.8)
. (2.8) .
. решение уравнения (2.7) получается с помощью
решение уравнения (2.7) получается с помощью  кратного интегрирования функции
кратного интегрирования функции 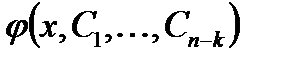 (см. п. 2.2.1).
(см. п. 2.2.1). не содержащего явно искомой функции y подстановка
не содержащего явно искомой функции y подстановка  , тогда
, тогда  преобразует данное уравнение в уравнение I порядка
преобразует данное уравнение в уравнение I порядка 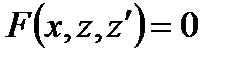
 .
. и
и  . Положим
. Положим  , тогда
, тогда  и уравнение будет иметь вид:
и уравнение будет иметь вид:  . Это линейное уравнение первого порядка (см. п.1.4.). Его общее решение имеет вид
. Это линейное уравнение первого порядка (см. п.1.4.). Его общее решение имеет вид  . Так как
. Так как  , то для отыскания искомого общего решения надо проинтегрировать уравнение
, то для отыскания искомого общего решения надо проинтегрировать уравнение  . Таким образом,
. Таким образом, ,
, .
. , где
, где  - произвольные постоянные, является общим решением заданного уравнения.
- произвольные постоянные, является общим решением заданного уравнения. . (2.9)
. (2.9) . В этом случае примем
. В этом случае примем  за независимую переменную и введем новую функцию
за независимую переменную и введем новую функцию  . Считая, что
. Считая, что  есть функция от
есть функция от  и через посредство
и через посредство  зависит от
зависит от  и, применяя правило дифференцирования сложных функций, получим для производных от
и, применяя правило дифференцирования сложных функций, получим для производных от  по
по  выражения
выражения ,
, ,
, .
. и т.д., увидим, что в новых переменных порядок уравнения будет
и т.д., увидим, что в новых переменных порядок уравнения будет  , т.е. на единицу ниже.
, т.е. на единицу ниже. - его решение, то нахождение общего интеграла данного уравнения сводится к интегрированию
- его решение, то нахождение общего интеграла данного уравнения сводится к интегрированию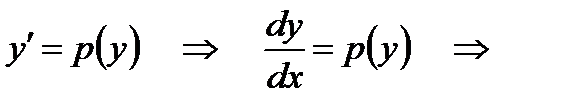
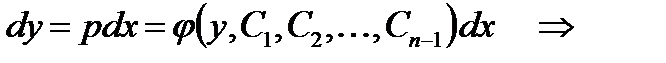
 .
. .
. входит в качестве слагаемого к
входит в качестве слагаемого к  , а это означает, что всякую интегральную кривую можно перемещать параллельно оси
, а это означает, что всякую интегральную кривую можно перемещать параллельно оси  .
.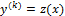

 , а затем
, а затем  .
. подстановка
подстановка 
 сводит уравнение к уравнению первого порядка
сводит уравнение к уравнению первого порядка 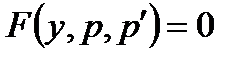
 .
. и подставим в исходное уравнение, тогда получим
и подставим в исходное уравнение, тогда получим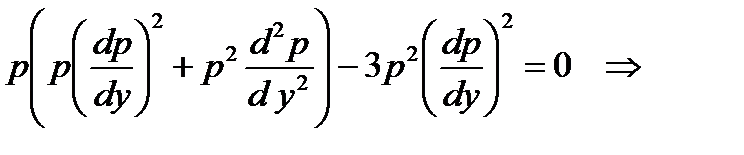
 .
. , при этом учтем теряемое решение
, при этом учтем теряемое решение  или
или  и получим
и получим .
. придем к уравнению
придем к уравнению .
. (при этом учитываем еще одно решение
(при этом учитываем еще одно решение  , т.е.
, т.е.  и
и  ), получим
), получим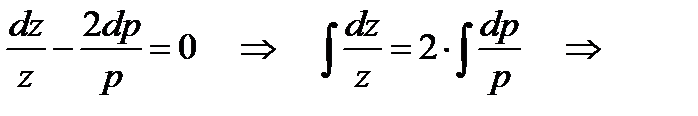
 .
. , находим
, находим  , или
, или  Окончательно получим
Окончательно получим , где
, где  .
. ).
).


