Линейные уравнения первого порядка
Определение. Линейным дифференциальным уравнением первого порядка называется уравнение вида
где По теореме существования и единственности решения задачи Коши (см. п.1.1) через каждую точку полосы
проходит одна и только одна интегральная кривая рассматриваемого уравнения. Если Это уравнение с разделяющимися переменными, его общее решение есть
где При
Пример 1 Проинтегрировать дифференциальное уравнение
Решение. Перепишем данное уравнение в виде
Уравнение (1.31) - неоднородное линейное дифференциальное уравнение. Однородное уравнение, соответствующее (1.31), есть уравнение вида
которое имеет общее решение
или
Общее решение ОДУ (1.31) будем искать в виде (1.32), где
Из (1.33) находим
Подставляя
или
Из последнего находим
Оно, очевидно, есть общее решение и уравнения (1.30). Пример 2 Найти интегральную кривую уравнения
проходящую через точку Решение. Считая
Уравнение (1.35) проинтегрируем методом Лагранжа. Общее решение однородного линейного уравнения, соответствующего (1.35), есть
или
Последнее соотношение перепишем в виде
Общее решение ОДУ (1.35) также будем искать в виде (1.36), при этом считаем
Подставим
или
Из последнего уравнения находим
где
Ясно, что (1.37) есть общий интеграл и уравнения (1.34). Выделим из него частное решение ОДУ (1.34), удовлетворяющее начальным данным
Уравнение (1.28) можно решать следующим образом: будем искать решение уравнения в виде произведения двух функций
Найдем производную подставляя в уравнение 1.28 получаем
Сгруппируем слагаемые в левой части (1.38)
предположим, что функция
Это уравнение с отделяющимися переменными
Нам достаточно иметь только одно решение этого уравнения, поэтому в первой части мы пишем одну первообразную (c=0) Найдя функцию
Уравнение (1.41) также уравнение с разделяющимися переменными. Таким образом указанный прием (способ Бернулли) сводит решение линейного уравнения (1.28) к решению двух уравнений с разделяющимися переменными, т.е. к решению системы
Линейные уравнения не имеют особых решений. Пример 3 Найти общее решение уравнения
Решение. В данном примере Составляем систему (1.42) из уравнения Получаем Решаем I уравнение системы
находим функцию
Подставляем найденные u и v в формулу
|

 (1.28)
(1.28) – непрерывные на некотором интервале
– непрерывные на некотором интервале 
 функции.
функции.
 то уравнение (1.28) называется однородным линейным дифференциальным уравнением.
то уравнение (1.28) называется однородным линейным дифференциальным уравнением.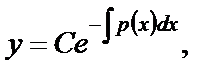 (1.29)
(1.29) произвольная постоянная, а
произвольная постоянная, а  означает первообразную функцию для функции
означает первообразную функцию для функции 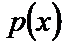 .
. уравнение (1.28) называется неоднородным. При интегрировании неоднородного линейного дифференциального уравнения (1.28) применяют так называемый метод вариации произвольной постоянной или метод Лагранжа. Этот метод состоит в том, что общее решение ОДУ (1.28) ищут в таком же виде, что и общее решение соответствующего ему однородного уравнения, т.е. в виде (1.29). Но при этом считают произвольную постоянную
уравнение (1.28) называется неоднородным. При интегрировании неоднородного линейного дифференциального уравнения (1.28) применяют так называемый метод вариации произвольной постоянной или метод Лагранжа. Этот метод состоит в том, что общее решение ОДУ (1.28) ищут в таком же виде, что и общее решение соответствующего ему однородного уравнения, т.е. в виде (1.29). Но при этом считают произвольную постоянную 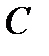 непрерывно дифференцируемой функцией от
непрерывно дифференцируемой функцией от  . Иллюстрацию метода проведем на следующих примерах.
. Иллюстрацию метода проведем на следующих примерах. . (1.30)
. (1.30) (1.31)
(1.31)
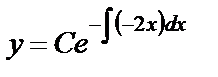
 (1.32)
(1.32) считаем непрерывно дифференцируемой функцией от
считаем непрерывно дифференцируемой функцией от  , т.е. в виде
, т.е. в виде . (1.33)
. (1.33) .
. и найденное выражение
и найденное выражение  в уравнение (1.31), получаем следующее дифференциальное уравнение для определения
в уравнение (1.31), получаем следующее дифференциальное уравнение для определения  :
:
 .
. где
где  произвольная постоянная. Подставив
произвольная постоянная. Подставив  в (1.33), получим общее решение ОДУ (1.31):
в (1.33), получим общее решение ОДУ (1.31):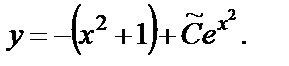
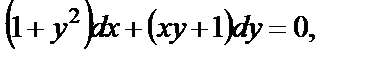 (1.34)
(1.34) .
. функцией от
функцией от  , приведем данное уравнение к линейному относительно
, приведем данное уравнение к линейному относительно  . Для этого обе части (1.34) умножим на функцию
. Для этого обе части (1.34) умножим на функцию  тогда будем иметь
тогда будем иметь . (1.35)
. (1.35)

 . (1.36)
. (1.36) С учетом последнего из (1.36) находим
С учетом последнего из (1.36) находим 
 .
. и
и  в (1.35), получим дифференциальное уравнение для определения
в (1.35), получим дифференциальное уравнение для определения 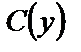 :
:
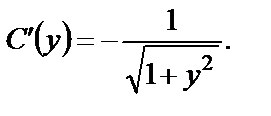
 ,
, произвольная постоянная. Подставим
произвольная постоянная. Подставим  вместо
вместо  в (1.36), найдем общее решение уравнения (1.35)
в (1.36), найдем общее решение уравнения (1.35) . (1.37)
. (1.37)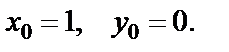 Для этого положим в (1.37)
Для этого положим в (1.37) 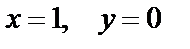 , тогда имеем
, тогда имеем  Следовательно, искомая интегральная кривая уравнения (1.34) задается уравнением
Следовательно, искомая интегральная кривая уравнения (1.34) задается уравнением .
. и
и 
 - (подстановка Бернулли)
- (подстановка Бернулли)
 (1.38)
(1.38)
 (1.39)
(1.39)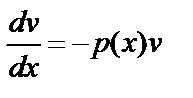


 (1.40)
(1.40) (1.41)
(1.41) (1.42)
(1.42)

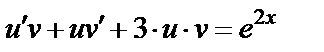

 ;
;  ;
; 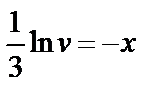 ;
; 
 (полагаем c=0)
(полагаем c=0)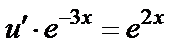 ;
; 

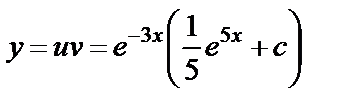 , получаем
, получаем