Определение. Уравнение с разделенными переменными – это уравнение вида
 или
или  , (1.8)
, (1.8)
где  и
и  функции, зависящие только от х и y соответственно, являющиеся непрерывными при рассматриваемых значения х и y.
функции, зависящие только от х и y соответственно, являющиеся непрерывными при рассматриваемых значения х и y.
Общим интегралом такого уравнения является равенство
 ,
,
в котором под выражениями  понимаются произвольные первообразные функций М и N, соответственно, С – произвольная постоянная.
понимаются произвольные первообразные функций М и N, соответственно, С – произвольная постоянная.
Пример 1 Проверить, что общим интегралом ОДУ 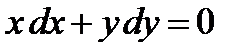 в области
в области  , является равенство
, является равенство
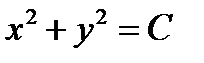 . (1.9)
. (1.9)
Решение. Действительно, проинтегрировав его левую часть, получим
 ,
,
следовательно, общим интегралом рассматриваемого уравнения является соотношение
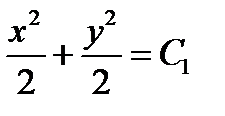 ,
,
откуда, в силу произвольности константы  , следует (1.9), где
, следует (1.9), где  .
.
Пример 2 Уравнение

при 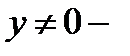 интегрируется так:
интегрируется так:
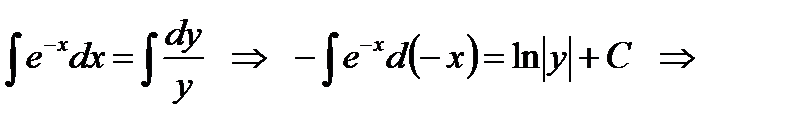
 или
или 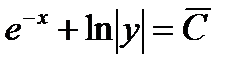 ,
,
где  , следовательно, общий интеграл имеет вид
, следовательно, общий интеграл имеет вид
 ,
,
где  произвольная константа.
произвольная константа.
Определение. Уравнение вида
 , (1.10)
, (1.10)
в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от х и только от y, называется уравнением с разделяющимися переменными.
Умножением обеих частей этого уравнения на функцию
 , (1.11)
, (1.11)
оно приводится к уравнению (1.8) с разделенными переменными. Поэтому общий интеграл ОДУ (1.10) есть
 . (1.12)
. (1.12)
Если уравнения  имеют действительные решения x=a и y=b, то функции
имеют действительные решения x=a и y=b, то функции 
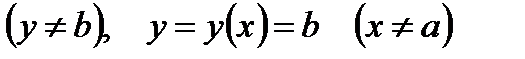 , являясь решением (1.10), могут не входить в общий интеграл (1.12) ни при каком конечном значении С, хотя при этом среди них могут быть частные решения (1.10), то есть последние при интегрировании оказываются потерянными. Точки вида х=а, y=b исключаются из интегральных кривых, соответствующих решениям
, являясь решением (1.10), могут не входить в общий интеграл (1.12) ни при каком конечном значении С, хотя при этом среди них могут быть частные решения (1.10), то есть последние при интегрировании оказываются потерянными. Точки вида х=а, y=b исключаются из интегральных кривых, соответствующих решениям  , так как в этих точках уравнение (1.10) не задано. Необходимо отметить также, что среди решений
, так как в этих точках уравнение (1.10) не задано. Необходимо отметить также, что среди решений  могут быть и особые решения ОДУ (1.10).
могут быть и особые решения ОДУ (1.10).
Пример 3 Проинтегрировать уравнение
 . (1.13)
. (1.13)
Решение. Обе части уравнения умножим на функцию 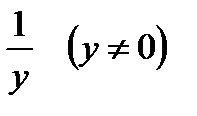 , тогда его можно записать в дифференциальной форме
, тогда его можно записать в дифференциальной форме
 . (1.14)
. (1.14)
Получили уравнение с разделенными переменными. Его общий интеграл при при  есть соотношение
есть соотношение
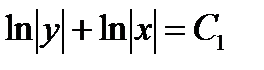 ,
,
где  произвольная постоянная. Константу
произвольная постоянная. Константу  представим в виде
представим в виде  , тогда
, тогда  , откуда имеем
, откуда имеем  или
или  . В последнем соотношении, в силу произвольности
. В последнем соотношении, в силу произвольности  , знаки модуля можно опустить. Следовательно,
, знаки модуля можно опустить. Следовательно,
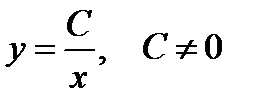 . (1.15)
. (1.15)
Очевидно, решение  уравнения (1.13) не входит в последнюю формулу ни при каком значении
уравнения (1.13) не входит в последнюю формулу ни при каком значении  , хотя соответствующая ему интегральная кривая лежит в областях существования и единственности решения задачи Коши этого уравнения, то есть решение
, хотя соответствующая ему интегральная кривая лежит в областях существования и единственности решения задачи Коши этого уравнения, то есть решение  оказалось потерянным. Однако оно входит в формулу (1.15) при
оказалось потерянным. Однако оно входит в формулу (1.15) при  . Поэтому, допуская в (1.15) и
. Поэтому, допуская в (1.15) и 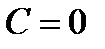 , получаем, что общее решение уравнения (1.13) при
, получаем, что общее решение уравнения (1.13) при 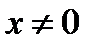 имеет вид
имеет вид
 ,
,
где  произвольная постоянная.
произвольная постоянная.
Заметим, что функция  является решением перевернутого по отношению к (1.13) уравнения
является решением перевернутого по отношению к (1.13) уравнения
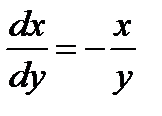 .
.
Пример 4 Найти решение дифференциального уравнения
 ,
,
удовлетворяющее начальному условию  .
.
Решение. Разделим переменные, умножив обе части уравнения на  . Имеем
. Имеем
 .
.
Интегрируя последнее уравнение, получаем

или
 .
.
Так как  , то в последнем соотношении
, то в последнем соотношении  . Отсюда находим общее решение данного уравнения в области
. Отсюда находим общее решение данного уравнения в области  :
:
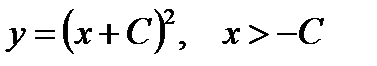 .
.
Выделим частное решение, удовлетворяющее начальному условию  . Для этого в формуле общего решения положим
. Для этого в формуле общего решения положим  , получим уравнение для определения значения константы
, получим уравнение для определения значения константы  . Из него находим
. Из него находим 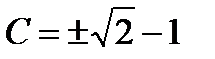 . Из двух, значений
. Из двух, значений  и
и 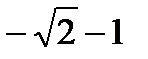 выбираем
выбираем 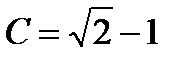 , так как точка
, так как точка  не лежит на кривой
не лежит на кривой  .
.
Итак, искомое решение есть
 .
.
Пример 5 Найти общий интеграл уравнения
 . (1.16)
. (1.16)
Решение. ОДУ (1.16) – это уравнение с разделяющимися переменными. Умножив обе части его на функцию
 ,
,
получим уравнение с разделенными переменными
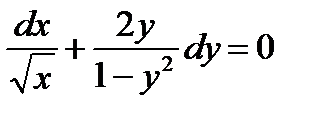 . (1.17)
. (1.17)
Общим интегралом последнего является соотношение
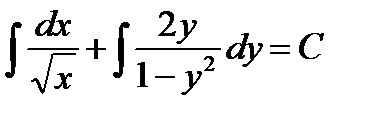
или
 . (1.18)
. (1.18)
Следовательно, (1.18) есть общий интеграл ОДУ (1.16).
Заметим, что формула (1.18) получена в предположении, что  . Функции
. Функции  и
и  являются, очевидно, решениями (1.16) и они не входят в (1.18) ни при каком конечном значении константы С. Покажем, что функции
являются, очевидно, решениями (1.16) и они не входят в (1.18) ни при каком конечном значении константы С. Покажем, что функции  являются частными, а функция
являются частными, а функция  – особым решением уравнения (1.16).
– особым решением уравнения (1.16).
Действительно, полупрямые 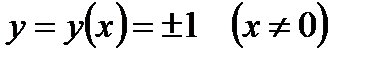 лежат в областях существования и единственности уравнения
лежат в областях существования и единственности уравнения
 , (1.19)
, (1.19)
получающегося из (1.16) разрешением относительно  . Значит, эти полупрямые есть частные решения ОДУ (1.19), а следовательно и (1.16). Записав общий интеграл (1.18) в иной форме, выделим из него эти частные решения. Положим в (1.18)
. Значит, эти полупрямые есть частные решения ОДУ (1.19), а следовательно и (1.16). Записав общий интеграл (1.18) в иной форме, выделим из него эти частные решения. Положим в (1.18)  , где
, где  произвольная константа, тогда (1.18) перепишется так:
произвольная константа, тогда (1.18) перепишется так:

или
 .
.
Отсюда имеем  и, в силу произвольности
и, в силу произвольности  ,
,
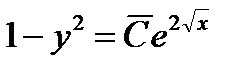 . (1.20)
. (1.20)
Соотношение (1.20) - также общий интеграл ОДУ (1.16). Оно получено в предположении 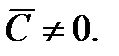 Очевидно, решения
Очевидно, решения  уравнения (1.16) получаются из (1.20) при значении
уравнения (1.16) получаются из (1.20) при значении  Но, как мы показали, эти решения – частные, следовательно, в (1.20) можно допускать и
Но, как мы показали, эти решения – частные, следовательно, в (1.20) можно допускать и  . Таким образом, частные решения
. Таким образом, частные решения  уравнения (1.16) получаются из общего интеграла (1.20) этого уравнения при
уравнения (1.16) получаются из общего интеграла (1.20) этого уравнения при 
Покажем сейчас, что функция 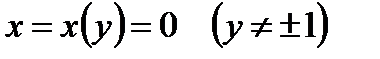 является особым решением уравнения (1.16). Отметим, во-первых, что соответствующая ей интегральная кривая не лежит в областях существования и единственности уравнения
является особым решением уравнения (1.16). Отметим, во-первых, что соответствующая ей интегральная кривая не лежит в областях существования и единственности уравнения
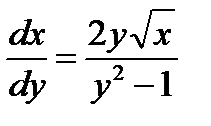 ,
,
перевернутого по отношению к (1.19), так как частная производная по  функции
функции  в точках прямой
в точках прямой  обращается в бесконечность. Убедимся теперь в том, что через каждую точку интегральной кривой
обращается в бесконечность. Убедимся теперь в том, что через каждую точку интегральной кривой 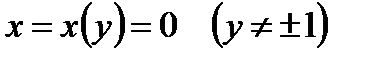 проходит по крайней мере две интегральные кривые уравнения (1.16). Выберем произвольно точку
проходит по крайней мере две интегральные кривые уравнения (1.16). Выберем произвольно точку  на этой кривой и ее координаты подставим в общий интеграл (1.20). Будем иметь соотношение для определения
на этой кривой и ее координаты подставим в общий интеграл (1.20). Будем иметь соотношение для определения  :
:
 .
.
Отсюда находится кривая 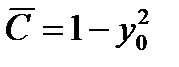 . Таким образом, интегральная кривая
. Таким образом, интегральная кривая 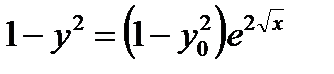 также проходит через точку
также проходит через точку  , то есть функция
, то есть функция 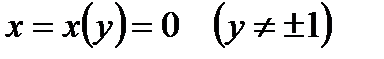 – особое решение ОДУ (1.16).
– особое решение ОДУ (1.16).

 или
или  , (1.8)
, (1.8) и
и  функции, зависящие только от х и y соответственно, являющиеся непрерывными при рассматриваемых значения х и y.
функции, зависящие только от х и y соответственно, являющиеся непрерывными при рассматриваемых значения х и y. ,
, понимаются произвольные первообразные функций М и N, соответственно, С – произвольная постоянная.
понимаются произвольные первообразные функций М и N, соответственно, С – произвольная постоянная.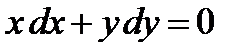 в области
в области  , является равенство
, является равенство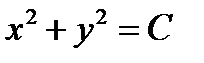 . (1.9)
. (1.9) ,
,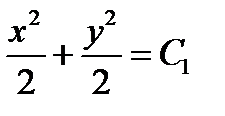 ,
, , следует (1.9), где
, следует (1.9), где  .
.
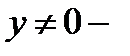 интегрируется так:
интегрируется так: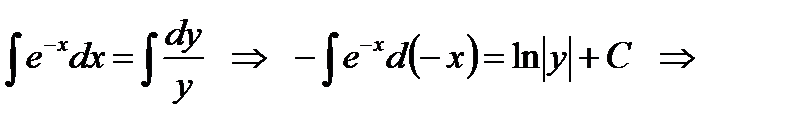
 или
или 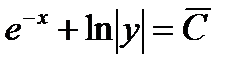 ,
, , следовательно, общий интеграл имеет вид
, следовательно, общий интеграл имеет вид ,
, произвольная константа.
произвольная константа. , (1.10)
, (1.10) , (1.11)
, (1.11) . (1.12)
. (1.12) имеют действительные решения x=a и y=b, то функции
имеют действительные решения x=a и y=b, то функции 
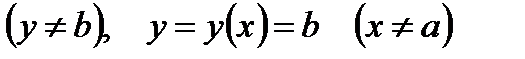 , являясь решением (1.10), могут не входить в общий интеграл (1.12) ни при каком конечном значении С, хотя при этом среди них могут быть частные решения (1.10), то есть последние при интегрировании оказываются потерянными. Точки вида х=а, y=b исключаются из интегральных кривых, соответствующих решениям
, являясь решением (1.10), могут не входить в общий интеграл (1.12) ни при каком конечном значении С, хотя при этом среди них могут быть частные решения (1.10), то есть последние при интегрировании оказываются потерянными. Точки вида х=а, y=b исключаются из интегральных кривых, соответствующих решениям  , так как в этих точках уравнение (1.10) не задано. Необходимо отметить также, что среди решений
, так как в этих точках уравнение (1.10) не задано. Необходимо отметить также, что среди решений  могут быть и особые решения ОДУ (1.10).
могут быть и особые решения ОДУ (1.10). . (1.13)
. (1.13)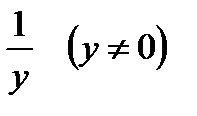 , тогда его можно записать в дифференциальной форме
, тогда его можно записать в дифференциальной форме . (1.14)
. (1.14) есть соотношение
есть соотношение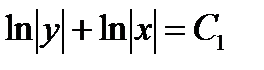 ,
, произвольная постоянная. Константу
произвольная постоянная. Константу  представим в виде
представим в виде  , тогда
, тогда  , откуда имеем
, откуда имеем  или
или  . В последнем соотношении, в силу произвольности
. В последнем соотношении, в силу произвольности  , знаки модуля можно опустить. Следовательно,
, знаки модуля можно опустить. Следовательно,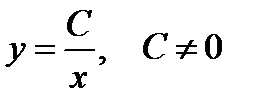 . (1.15)
. (1.15) уравнения (1.13) не входит в последнюю формулу ни при каком значении
уравнения (1.13) не входит в последнюю формулу ни при каком значении  , хотя соответствующая ему интегральная кривая лежит в областях существования и единственности решения задачи Коши этого уравнения, то есть решение
, хотя соответствующая ему интегральная кривая лежит в областях существования и единственности решения задачи Коши этого уравнения, то есть решение  оказалось потерянным. Однако оно входит в формулу (1.15) при
оказалось потерянным. Однако оно входит в формулу (1.15) при  . Поэтому, допуская в (1.15) и
. Поэтому, допуская в (1.15) и 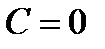 , получаем, что общее решение уравнения (1.13) при
, получаем, что общее решение уравнения (1.13) при 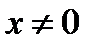 имеет вид
имеет вид ,
, произвольная постоянная.
произвольная постоянная. является решением перевернутого по отношению к (1.13) уравнения
является решением перевернутого по отношению к (1.13) уравнения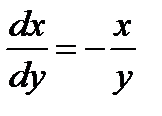 .
. ,
, .
. . Имеем
. Имеем .
.
 .
. , то в последнем соотношении
, то в последнем соотношении  . Отсюда находим общее решение данного уравнения в области
. Отсюда находим общее решение данного уравнения в области  :
: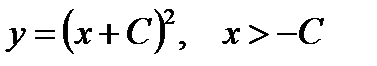 .
. . Для этого в формуле общего решения положим
. Для этого в формуле общего решения положим  , получим уравнение для определения значения константы
, получим уравнение для определения значения константы  . Из него находим
. Из него находим 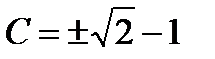 . Из двух, значений
. Из двух, значений  и
и 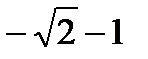 выбираем
выбираем 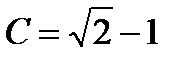 , так как точка
, так как точка  не лежит на кривой
не лежит на кривой  .
. .
. . (1.16)
. (1.16) ,
,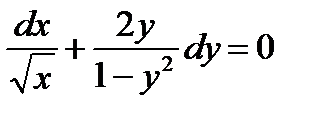 . (1.17)
. (1.17)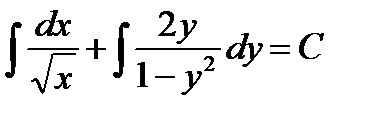
 . (1.18)
. (1.18) . Функции
. Функции  и
и  являются, очевидно, решениями (1.16) и они не входят в (1.18) ни при каком конечном значении константы С. Покажем, что функции
являются, очевидно, решениями (1.16) и они не входят в (1.18) ни при каком конечном значении константы С. Покажем, что функции  являются частными, а функция
являются частными, а функция  – особым решением уравнения (1.16).
– особым решением уравнения (1.16).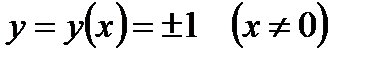 лежат в областях существования и единственности уравнения
лежат в областях существования и единственности уравнения , (1.19)
, (1.19) . Значит, эти полупрямые есть частные решения ОДУ (1.19), а следовательно и (1.16). Записав общий интеграл (1.18) в иной форме, выделим из него эти частные решения. Положим в (1.18)
. Значит, эти полупрямые есть частные решения ОДУ (1.19), а следовательно и (1.16). Записав общий интеграл (1.18) в иной форме, выделим из него эти частные решения. Положим в (1.18)  , где
, где  произвольная константа, тогда (1.18) перепишется так:
произвольная константа, тогда (1.18) перепишется так:
 .
. и, в силу произвольности
и, в силу произвольности  ,
,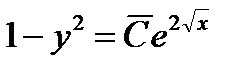 . (1.20)
. (1.20)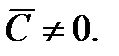 Очевидно, решения
Очевидно, решения  уравнения (1.16) получаются из (1.20) при значении
уравнения (1.16) получаются из (1.20) при значении  Но, как мы показали, эти решения – частные, следовательно, в (1.20) можно допускать и
Но, как мы показали, эти решения – частные, следовательно, в (1.20) можно допускать и  . Таким образом, частные решения
. Таким образом, частные решения  уравнения (1.16) получаются из общего интеграла (1.20) этого уравнения при
уравнения (1.16) получаются из общего интеграла (1.20) этого уравнения при 
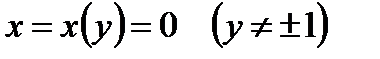 является особым решением уравнения (1.16). Отметим, во-первых, что соответствующая ей интегральная кривая не лежит в областях существования и единственности уравнения
является особым решением уравнения (1.16). Отметим, во-первых, что соответствующая ей интегральная кривая не лежит в областях существования и единственности уравнения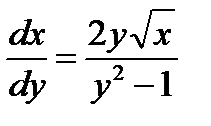 ,
, функции
функции  в точках прямой
в точках прямой  обращается в бесконечность. Убедимся теперь в том, что через каждую точку интегральной кривой
обращается в бесконечность. Убедимся теперь в том, что через каждую точку интегральной кривой 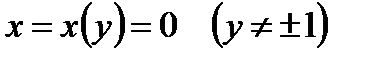 проходит по крайней мере две интегральные кривые уравнения (1.16). Выберем произвольно точку
проходит по крайней мере две интегральные кривые уравнения (1.16). Выберем произвольно точку  на этой кривой и ее координаты подставим в общий интеграл (1.20). Будем иметь соотношение для определения
на этой кривой и ее координаты подставим в общий интеграл (1.20). Будем иметь соотношение для определения  :
: .
.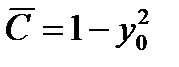 . Таким образом, интегральная кривая
. Таким образом, интегральная кривая 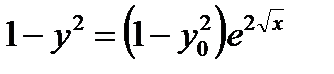 также проходит через точку
также проходит через точку  , то есть функция
, то есть функция 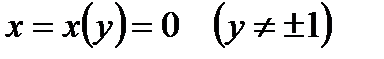 – особое решение ОДУ (1.16).
– особое решение ОДУ (1.16).


