Роль размеров системы
Ранее подчеркивалось, что понятие порога протекания имеет смысл лишь в бесконечной системе. В конечной системе порог протекания меняется от образца к образцу, т.е. является величиной случайной. Однако, значения, которые принимает эта случайная величина, с подавляющей вероятностью попадают в некоторую область с шириной Рассмотрим эксперимент с экранной сеткой, имеющей размеры L × L, схема которого изображена на рис.. Допустим, что сделано много опытов, использующих разные случайные последовательности блокируемых узлов, результатом которых явился набор порогов протекания. Напомним, что конфигурации блокированных узлов, полученные в разных опытах, совершенно не похожи друг на друга. Удобный способ рассуждения состоит в следующем. Вообразим бесконечную экранную сетку с заданной долей x неблокированных узлов. Представим, что на разные участки этой сетки накладывается: квадрат, имеющий размеры L × L, и изучается протекание с левой стороны этого квадрата на правую по неблокированным узлам, оказавшимся внутри этого квадрата (рис.7.19). Накладывая квадрат на разные участки бесконечной сетки, можно перебрать результаты разных опытов с конечной сеткой. В бесконечной экранной сетке протекание возникает точно при x = xc, но, как мы сейчас увидим, это совершенно не означает, что при x > xc обязательно есть протекание в квадрате L × L. При x > xc в бесконечной системе существует бесконечный кластер. Изобразим его скелет в виде рыболовной сети, показанной на рис.7.19. Для дальнейшего крайне важно соотношение между радиусом корреляции R и длиной квадрата L. Примем сначала, что L значительно превосходит R. Тогда (рис.7.19)внутри квадрата находится много ячеек сети бесконечного кластера, который обеспечивает протекание между сторонами квадрата. Эти ячейки могут иметь разные размеры, в сети бесконечного кластера могут быть большие дыры, но если в квадрате в среднем должно быть много ячеек, то вероятность того, что в кластере имеется дыра размером в целый квадрат, ничтожно мала. Поэтому делается следующий вывод: Если x > xc, то порог протекания квадрата не может находиться в области значений x, удовлетворяющей сильному неравенству L > > R(x). Эта область должна быть выше порога. Согласно формуле (7.7) при стремлении x к xc радис корреляции неограниченно возрастает и при каком-то значении x неизбежно сравнивается с L. Теперь о протекании внутри квадрата ничего определенного сказать нельзя. Все зависит от конкретной конфигурации блокированных узлов внутри него.
Рис. 7.21. Большие кластеры, заданные компьютером на квадратной решетке при p = 0, 53, т.е. ниже порога протекания по узлам
Пусть теперь x < xc и радиус корреляции значительно меньше, чем L. При x < xc и радиус корреляции представляет собой максимальную длину конечных кластеров. Если R < < L, то не существует такого кластера, который мог бы связать стороны квадрата. Поэтому делается еще один определенный вывод: Если x < xc, то порог протекания квадрата тоже не может находиться в области значений x, удовлетворяющей сильному неравенству L? R(x). Эта область должна быть ниже порога. Если x < xc, но величина x очень близка к xc, то радиус корреляции становится больше, чем L. В этом случае о протекании в квадрате нельзя сказать ничего определенного. В бесконечной системе существуют конечные кластеры размера, большего, чем L, но внутри них есть дыры такого же размера, и все зависит от конкретной конфигурации блокированных узлов внутри квадрата. Теперь можно оценить размер критической области в которой могут находиться значения порога протекания квадрата L × L. Согласно выводам (1) и (2) эта область должна определяться условием L ≤ R. Как видно из рис., чем больше L, тем уже эта область и тем теснее она прижата к порогу протекания для бесконечной системы. Ширина области определяется условием R (δ) = L. С помощью формулы (1) получаем
Внутри критической области, т.е. при | x – xc | пороги протекания квадратов с длиной L распределены однородно. Точка x = xc внутри этой области ничем не выделена. Действительно, это точка, в которой наступает протекание в бесконечной системе. Но установить, есть такое протекание или нет, работая с квадратом конечного размера, невозможно. Если L < R, то накладывая квадрат на разные участки бесконечной сетки, нельзя сказать, существуют в этой сетке только конечные кластеры или они уже слились и образуют бесконечный кластер. Изучение протекания в квадрате конечного размера позволяет лишь определить ширину критической области. В этом разделе обсуждались лишь плоские задачи. Однако все сказанное полностью переносится на задачи объемные. Ширина критической области для объемных задач также определяется формулой (7.8). Небольшая разница возникает, если выразить ширину δ не через размер системы L, а через полное число узлов
где C – численный коэффициент, который не может быть определен из столь простых соображений. Именно с помощью этой формулы в результате исследования найденной на ЭВМ зависимости
|

 , которая называется критической областью. При увеличении числа узлов в системе
, которая называется критической областью. При увеличении числа узлов в системе 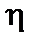 ширина этой области уменьшается по степенному закону, так что при
ширина этой области уменьшается по степенному закону, так что при  порог протекания приобретает четкий смысл, превращаясь из случайной величины в величину достоверную.
порог протекания приобретает четкий смысл, превращаясь из случайной величины в величину достоверную.
 . Эти кластеры соединены в основном однократно.
. Эти кластеры соединены в основном однократно. = L или
= L или (7.8)
(7.8) . Дело в том, что
. Дело в том, что  , где a – период решетки, d – размерность пространства. Поэтому согласно (7.8)
, где a – период решетки, d – размерность пространства. Поэтому согласно (7.8) (7.9)
(7.9) был впервые определен индекс радиуса корреляции плоской задачи. Оказалось, что
был впервые определен индекс радиуса корреляции плоской задачи. Оказалось, что  = 1, 33. (число 2 - индекс двумерной системы.) Для трехмерных задач индекс
= 1, 33. (число 2 - индекс двумерной системы.) Для трехмерных задач индекс  иной:
иной:  = 0, 8 ÷ 0, 9.
= 0, 8 ÷ 0, 9.


