Поверхностные интегралы
4.1.Поверхностный интеграл I рода
Пусть поверхность S задана в пространстве уравнением z = z (x, y), где функция z (x, y) имеет непрерывные частные производные в некоторой области DÍ R 2. В этом случае будем называть поверхность гладкой. Пусть теперь поверхность S содержится в области определения непрерывной функции f (x, y, z). Разобьем поверхность на n частей S1, S2, …, Sn; обозначим через DSk площадь части Sk, а через d k – ее диаметр. Пусть d = Определение. Если существует предел интегральных сумм (*) при d ®0, не зависящий от разбиения, то он называется поверхностным интегра л ом I рода функции f (x, y, z) по поверхности S и обозначается Примем без доказательства следующие свойства поверхностного интеграла I рода. 1о. 2о. 3о. + Напомним, что свойства 2о и 3о – это свойства линейности. 4о. Если на поверхности S выполняется неравенство f (x, y, z)³ g (x, y, z), то 5о. Если поверхность S разбита на части S1 и S2, не имеющие общих внутренних точек, то 6о. 7о. Если функция f (x, y, z) непрерывна на поверхности S и s – площадь поверхности, то существует такая точка (x, h, z)Î S, что Можно доказать, что если поверхность S задана уравнением z = z (x, y), (x, y)Î D, то вычисление поверхностного интеграла I рода сводится к вычислению двойного интеграла: 4.2.Поверхностный интеграл II рода
Пусть опять поверхность S задана уравнением z = z (x, y), где функция z (x, y) имеет непрерывные частные производные в некоторой области DÍ R 2. Пусть S содержится в области определения непрерывной функции f (x, y, z). Зафиксируем одну из сторон поверхности и разобьем ее на n частей S1, S2, …, Sn. Обозначим через Dsk площадь проекции Sk на плоскость x O y, взятую со знаком «+», если нормаль к выбранной стороне поверхности составляет с осью O z острый угол, и со знаком «–» – в противном случае. В каждой части Sk выберем точку ( Определение. Если существует предел интегральных сумм (*) при d ®0 (d – диаметр разбиения), не зависящий от разбиения, то он называется поверхностным интегралом II рода функции f (x, y, z) по переменным х и у по выбранной стороне поверхности S и обозначается В общем виде поверхностный интеграл II рода имеет вид: Поверхностный интеграл II рода обладает свойствами линейности и аддитивности. Он меняет знак при перемене стороны поверхности. Вычисление поверхностного интеграла II рода сводится к вычислению двойного интеграла следующим образом. Рассмотрим интеграл по х и у. Пусть поверхность S задана уравнением z = z (x, y) и пусть D xy – проекция S на плоскость х О у. Выберем сторону поверхности так, чтобы нормаль к ней образовывала с осью О z острый угол. Тогда
4.3.Формула Остроградского-Гаусса
Формула Остроградского-Гаусса устанавливает связь между поверхностным интегралом II рода по замкнутой поверхности и тройным интегралом по области, ограниченной этой поверхностью:
Здесь V – область, ограниченная гладкой поверхностью S; функции P(x, y, z), Q(x, y, z) и R(x, y, z) непрерывны в этой области вместе со своими частными производными; интегрирование ведется по внешней стороне. Пример. Вычислим По формуле Остроградского-Гаусса
=
4.4.Формула Стокса
Формула Стокса устанавливает связь между поверхностным и криволинейным интегралами II рода:
= Пример. Вычислим Перепишем уравнение окружности в параметрической форме: x =Rcos t, y =Rsin t, z =0, t Î [0; 2π ]. Тогда = = – По формуле Стокса = = =
|

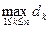 – диаметр разбиения. Пусть (
– диаметр разбиения. Пусть (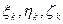 )Î Sk. Составим интегральную сумму: S=
)Î Sk. Составим интегральную сумму: S= 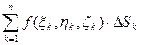 . (*)
. (*)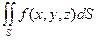 .
.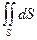 равен площади поверхности S.
равен площади поверхности S.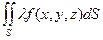 = l
= l 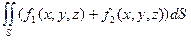 =
= 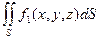 +
+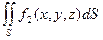 .
.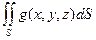 .
.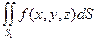 +
+ 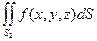 (свойство аддитивности).
(свойство аддитивности).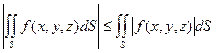 .
. .
.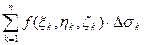 . (*)
. (*)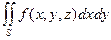 . Аналогично определяются поверхностные интегралы II рода по переменным у и z или х и z.
. Аналогично определяются поверхностные интегралы II рода по переменным у и z или х и z.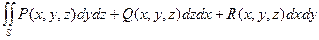 . Если выбранная сторона поверхности имеет вектор нормали
. Если выбранная сторона поверхности имеет вектор нормали 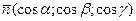 , то поверхностный интеграл второго рода связан с интегралом первого рода формулой:
, то поверхностный интеграл второго рода связан с интегралом первого рода формулой: 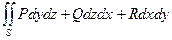 =
= 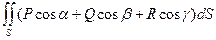 .
.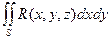 =
=  . Если же выбрать другую сторону поверхности, то интеграл берется с минусом. Аналогично вычисляется интеграл и по другим парам координат.
. Если же выбрать другую сторону поверхности, то интеграл берется с минусом. Аналогично вычисляется интеграл и по другим парам координат.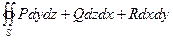 =
= 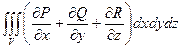 .
.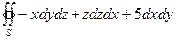 , где S – внешняя сторона поверхности пирамиды, ограниченной плоскостями 2 х –3 у + z =6, x =0, y =0, z =0.
, где S – внешняя сторона поверхности пирамиды, ограниченной плоскостями 2 х –3 у + z =6, x =0, y =0, z =0.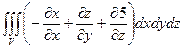 =
=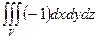 = –
= – 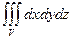 . Этот тройной интеграл равен объему пирамиды с вершинами A(3; 0; 0), B(0; –2; 0), C(0; 0; 6), O(0; 0; 0). V=
. Этот тройной интеграл равен объему пирамиды с вершинами A(3; 0; 0), B(0; –2; 0), C(0; 0; 6), O(0; 0; 0). V=  = 6. Значит,
= 6. Значит,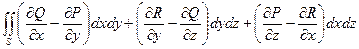 =
=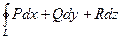 . Здесь S – область, ограниченная гладкой кривой L; функции P(x, y, z), Q(x, y, z) и R(x, y, z) непрерывны на этой поверхности вместе со своими частными производными; интегрирование ведется в положительном направлении (то есть S остается слева).
. Здесь S – область, ограниченная гладкой кривой L; функции P(x, y, z), Q(x, y, z) и R(x, y, z) непрерывны на этой поверхности вместе со своими частными производными; интегрирование ведется в положительном направлении (то есть S остается слева).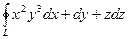 , где L – окружность х 2+ у 2=R2 в плоскости z =0, сначала непосредственно, а затем по формуле Стокса.
, где L – окружность х 2+ у 2=R2 в плоскости z =0, сначала непосредственно, а затем по формуле Стокса. +
+ 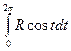 =
=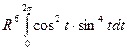 +0 = –
+0 = –  .
.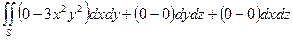 =
=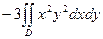 , где D – круг (поверхность S совпадает со своей проекцией на плоскость х О у). Вычислим двойной интеграл с помощью полярной замены:
, где D – круг (поверхность S совпадает со своей проекцией на плоскость х О у). Вычислим двойной интеграл с помощью полярной замены: 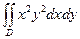 =
=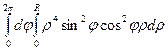 =
= 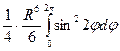 =
=  . Значит, исходный интеграл равен –
. Значит, исходный интеграл равен – 


