Лінійна функціяV 0(x) = (x – C w)/(s – b /s2) (4.31) є одним із розв’язків цього рівняння. Загальний розв’язок (4.29) записують як суму V 0(x) і розв’язок відповідного однорідного
Очевидно, що (4.32) має два лінійно незалежних розв’язки — е l х і е m х. Тут
Величини l, m — це корені відповідного характеристичного рівняння. Отже, загальний розв’язок (4.29) має вигляд: V (x) = V 0(x) + Ce l x + C 0 e m x. З (4.33) бачимо, що m > 0 > l. Отже, коли C 0 ¹ 0, то функція V (x), якщо х ® +¥,експоненціально зростатиме до +¥ або експоненціально спадатиме до –¥. Порівнюючи з детермінованим випадком, бачимо, що функція V (x) має зростати не швидше за x (t). Це можливо лише тоді, коли C 0 = 0. Згідно з умовою V (0) = 0 маємо C = – V 0(x). Далі запишемо V (x) = x /d – (C w/d + b /d2) [1 – e l x ]. (4.34) Зокрема, математичне сподівання інтегрально дисконтованого доходу від функціонування об’єкта з моменту, коли почалася на ньому відповідальна діяльність, після того як придбав його у власність даний підприємець, можна обчислити за формулою (4.34) за умови, що х = Х, тобто
Агрегування впливу випадкових чинників у один показник. Зауважимо, що коли w = k = s = 0 i Rj = R, то формула (4.34) перетворюється у формулу (4.24). Очевидно, що реальна динаміка доходу підприємства не завжди збігається з лінійною моделлю (4.22). Тоді зручніше обмежитися прогнозуванням динаміки середнього значення доходу, агрегувавши в один показник усю наявну інформацію про вплив випадкових чинників. У розвинутих країнах вплив чинників ризику і невизначеності враховується, по суті, встановленням відповідної норми дисконту (про що вже йшлося раніше). Для того щоб обчислення за формулами (4.24) і (4.34) з нормами дисконту R i Rj давали однакові результати, має задовольнятися рівняння
Уведемо такі позначення: С w/ X = g, d(s T / C)2 = n, d T = a, RT = r. (4.36) Співвідношення (4.35) можна подати у вигляді:
Отже, щоб визначити невідому норму дисконту, потрібно спочатку згідно з вихідною інформацією знайти ρ (розв’язок рівняння (4.37)) і, нарешті, обчислити R:
Це означає, що норма дисконту R з урахуванням ризику відрізняється від δ коригуючим коефіцієнтом Можна поглиблено проаналізувати вплив кожного з уведених чинників ризику. Сформулюймо такий важливий висновок з побудованої моделі: норму дисконту R, знайдену розглянутим способом, не можна подати ні у вигляді сум безризикової складової Rj та деякої надбавки, яка враховує ризик (премія за ризик) і є незалежною від Rj, ні у вигляді добутку цієї складової і якогось більшого від одиниці коефіцієнта, який не залежить від Rj і враховує ризик. Умовний приклад розрахунків норми дисконту з урахуванням чинників ризику. За одиницю вимірювання часу візьмемо один рік. Вважатимемо, що «збої» у виробництві виникають у середньому один раз на рік:
Поява нових технологій, упровадження яких зробить розглядуване виробництво збитковим, можна вважати малоймовірним. Якщо припустити, що такі «революції» в технології відбуваються в середньому три рази за сторіччя, то можна брати k = 0,03. Запишемо співвідношення для параметрів, які входять до рівняння (4.37):
У цьому разі R залежатиме лише від Rf і T та співвідношення Порівнювання значень R та Rj підтверджує висновок про неадитивність і немультиплікативність впливу чинників ризику на норму дисконту.
|

 (4.32)
(4.32) . (4.33)
. (4.33) .
. (4.35)
(4.35) (4.37)
(4.37) (4.38)
(4.38) . Значення цього коефіцієнта, як бачимо, залежить лише від a, g та n.
. Значення цього коефіцієнта, як бачимо, залежить лише від a, g та n.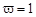 , а час на ліквідацію наслідків збою підлягає експоненційному закону розподілу із середнім значенням q = 0,04 (приблизно двом тижням). Припустимо, що витрати, пов’язані з ліквідацією наслідків «збою», пропорційні витратам в одиницю часу, причому кожен день «збою» не лише призводить до відсутності відповідного доходу, а й потребує додаткових витрат, що становлять 50 % початкового доходу Х. За даних передумов із (4.26) та (4.27) знайдемо:
, а час на ліквідацію наслідків збою підлягає експоненційному закону розподілу із середнім значенням q = 0,04 (приблизно двом тижням). Припустимо, що витрати, пов’язані з ліквідацією наслідків «збою», пропорційні витратам в одиницю часу, причому кожен день «збою» не лише призводить до відсутності відповідного доходу, а й потребує додаткових витрат, що становлять 50 % початкового доходу Х. За даних передумов із (4.26) та (4.27) знайдемо:




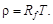
 .
.


