Стерический фактор и каталитическая активность.
Стерический или геометрический фактор - один из важнейших параметров, влияющих на хемосорбцию, а, следовательно, и на каталитическую эффективность. Стерический фактор проявляется в геометрическом соответствии расположения атомов в молекуле адсорбата и атомов на поверхности катализатора. Еще в 1929 г. Баландин А.А. выдвинул мультиплетную теорию, объясняющую каталитическую активность на базе геоиетрического строения молекулы реагента и кристаллической решетки катализатора. Суть мультиплетной теории состоит в следующем. При катализе происходит наложение (хемосорбция) группы атомов молекулы субстрата (называемых индексной группой) на группу активных атомов (центров) поверхности катализатора (называемых мультиплет) с образованием промежуточного мультиплетного комплекса. Например, при гидрировании двойной связи в олефинах происходит хемосорбция с образованием промежуточного мультиплетного комплекса на поверхности металла:
В данном случае индексной группой является этиленовая группа С=С, мультиплетом - пара активных центров М-М. Изучая скорость гидрирования коричной кислоты на металлах, был обнаружен максимум скорости на Rh для следующего ряда металлов: Ni, Rh, Pd, Pt, Ru, Os. Согласно мультиплетной теории Баландина, объяснение этому факту следующее: В образующемся мультиплетном комплексе угол М-С-С должен быть близок к тетраэдрическому (109о), в этом случае наиболее легко идет образование гидрированной молекулы. Учитывая, что длина С=С связи 1,54 Ао, и зная межатомные расстояния в испытуемых катализаторах, простым геометрическим расчетом можно убедиться, что в случае Rh угол в трапеции МССМ наиболее близок к тетраэдрическому. Примером решающего значения геометрического фактора на протекание каталитических служат ферментативно-каталитические реакции, протекающие по так называемому механизму "ключ-замок" ("key-keyhole"). Суть его в том, что реакция протекает лишь при строгом геометрическом соответствии реагента и катализатора (фермента). Такие реакции протекают со 100%-ной селективностью. К сожалению для промышленных гетерогенных катализаторов такая селективность не достижима.
|

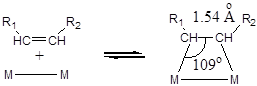 (5.27)
(5.27)


