Кодирование параметров задачи в генетическом алгоритмеВыбор исходной популяции связан с представлением параметров задачи в форме хромосом, т.е. с так называемым хромосомным представлением. Это представление определяется способом кодирования. В классическом генетическом алгоритме применяется двоичное кодирование, т.е. аллели всех генов в хромосоме равны 0 или 1. Длина хромосом зависит от условий задачи, точнее говоря от количества точек в пространстве поиска. Например, в рассмотренном в начале данной главы примере с функцией f (x) = 2 x 2+1 переменная x принимала целые значения из интервала [0, 15]. Пусть теперь x принимает целые значения из интервала [0, 31]. Для применения генетического алгоритма необходимо, прежде всего, закодировать значения переменной x в виде двоичных последовательностей. Очевидно, что целые числа из интервала [0, 31] можно представить в двоичной системе счисления. Число 0 при этом записывается как 00000, а 15 – как 11111. В данном случае хромосомы принимают вид двоичных последовательностей, состоящих из 5 битов, т.е. цепочками длиной 5. Рассмотрим общий случай. Пусть для заданной функции f (x) = 2 x 2+1 переменная x принимает действительные значения из интервала [ a, b ], где а =0, b =3,1. Допустим, что необходимо получить решение с точностью до одного знака после запятой. Поиск решения сводится к просмотру пространства, состоящего из 32 точек 0,0 0,1... 2,9 3,0 3,1. Эти точки (фенотипы) можно представить в виде хромосом (генотипов), если использовать бинарные пятизвенные цепочки, поскольку с помощью 5 битов можно получить 25 = 32 различных кодовых комбинации. Следовательно, можно использовать такое же множество кодовых последовательностей, как и в предыдущем примере, причем хромосома [00000] будет соответствовать числу 0,0, хромосома [00001] – числу 0,1 и т.д., вплоть до хромосомы [11111], соответствующей числу 3,1. Заметим, что если бы в данном примере требовалось получение решения с точностью, превышающей один знак после запятой, то интервал [0, 3,1] необходимо было бы разбить на большее количество подинтервалов, и для кодирования соответственно большего количества чисел потребовались более длинные хромосомы (с длиной, превышающей 5 битов). Аналогично, расширение области определения переменной х также потребует применения более длинных хромосом. Таким образом, длина хромосом зависит от ширины области определения х и от требуемой точности решения задачи. Представим теперь задачу в самом общем виде. Допустим, что производится поиск максимума функции f (x 1, х2,..., х n)>0 для
определяет необходимую и достаточную длину двоичной последовательности, требуемой для кодирования числа из интервала Пусть уi обозначает десятичное значение двоичной последовательности, кодирующей число хi. Значение хi можно представить выражением
Таким способом задаются фенотипы, соответствующие кодовым последовательностям с длиной тi. Полученное выражение – это следствие из простого линейного отображения интервала
|

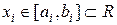 , i =1..n и требуется найти решение с точностью до q знаков после запятой для каждой переменной
, i =1..n и требуется найти решение с точностью до q знаков после запятой для каждой переменной  . В такой ситуации необходимо разбить интервал
. В такой ситуации необходимо разбить интервал 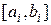 на
на  одинаковых подинтервалов. Это означает применение дискретизации с шагом
одинаковых подинтервалов. Это означает применение дискретизации с шагом 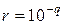 . Наименьшее натуральное число тi, удовлетворяющее неравенству
. Наименьшее натуральное число тi, удовлетворяющее неравенству
 .
.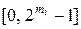 , где
, где  – десятичное число, закодированное двоичной последовательностью длиной тi и составленной только из единиц, а 0 – это десятичное значение двоичной последовательности длиной тi, составленной только из нулей.
– десятичное число, закодированное двоичной последовательностью длиной тi и составленной только из единиц, а 0 – это десятичное значение двоичной последовательности длиной тi, составленной только из нулей.


