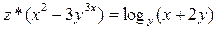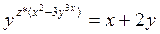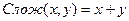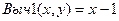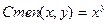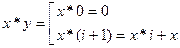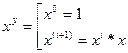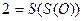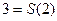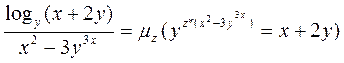3.1. Теоретические сведения о рекурсивных функциях
Примитивно-рекурсивными функциями называются функции, которые можно выразить через элементарные применением конечное число раз операторов суперпозиции и примитивной рекурсии.
Частично-рекурсивными функциями называются функции, которые можно выразить через элементарные применением конечное число раз операторов суперпозиции, примитивной рекурсии и минимизации.
Элементарные функции:
- Ноль – функция без аргументов, всегда возвращает ноль –

- Инкремент – функция повышения значения переменной на единицу, возвращает x+1 –

- Проекция – возвращает i-тую проекцию вектора переменных (то есть i-тую переменную) -
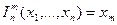
Операторы:
- Суперпозиция – оператор, позволяющий передавать функции в качестве параметра значение, возвращённое другой функцией.
Пример: 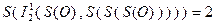
- Примитивная рекурсия – оператор, позволяющий вычислять значение
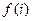 на основе
на основе 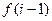 . При применении оператора примитивной рекурсии к функции
. При применении оператора примитивной рекурсии к функции 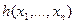 задаются две функции
задаются две функции  и
и  такие, что:
такие, что:
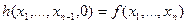
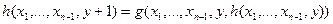
- Оператор минимизации – оператор, осуществляющий последовательный перебор всех возможных значений переменной пока её значение не будет удовлетворять некоторому условию. Формально – для заданной
 находит
находит 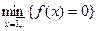 . Если
. Если  , то оператор минимизации зацикливается и функция не выполняется. На практике используется оператор минимизации вида
, то оператор минимизации зацикливается и функция не выполняется. На практике используется оператор минимизации вида 
3.2. Дерево структурного анализа
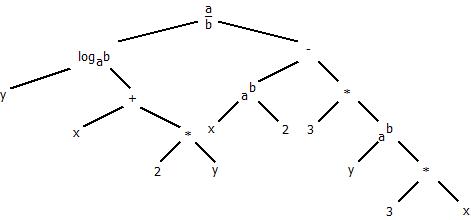
3.3. Доказательство ЧРФ
Пусть 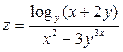 . Тогда:
. Тогда:
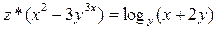
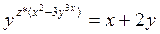
Докажем действия. Введём функции для каждой операции
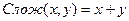

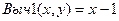

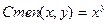


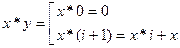

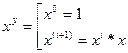
Докажем константы:
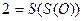
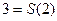
Применим оператор минимизации:
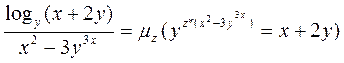



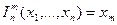
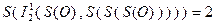
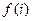 на основе
на основе 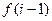 . При применении оператора примитивной рекурсии к функции
. При применении оператора примитивной рекурсии к функции 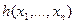 задаются две функции
задаются две функции  и
и  такие, что:
такие, что: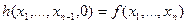
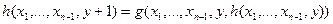
 находит
находит 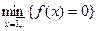 . Если
. Если  , то оператор минимизации зацикливается и функция не выполняется. На практике используется оператор минимизации вида
, то оператор минимизации зацикливается и функция не выполняется. На практике используется оператор минимизации вида 

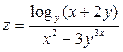 . Тогда:
. Тогда: