| №
| Запитання
| Розділ. Параграф.
|
| 1.
| Знайти дисперсію функції 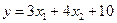 , якщо , якщо 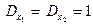 . .
| Р.2:П.3
|
|
| а) 25
б) 53
в) 35
г) 10
д) 0
|
|
| 2.
| Знайти математичне сподівання 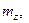 якщо якщо 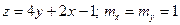 . .
| Р.2:П.3
|
|
| а) 2
б) 4
в) 5
г) 6
д) 0
|
|
| 3.
| Знайти дисперсію функції 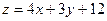 , якщо , якщо 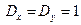 . .
| Р.2:П.3
|
|
| а) 19
б) 7
в) 5
г) 25
д) 0
|
|
| 4.
| Виміряні дві лінії: одна довжиною 210м з середньою квадратичною похибкою 4мм, друга – 180м з середньою квадратичною похибкою 3мм. З якою точністю обчислюватимуться віддалі, що рівні сумі двох ліній?
| Р.1:П.6
|
|
| а) 5 мм
б) 10 мм
в) 15 мм
г) 20 мм
д) 0 мм
|
|
| 5.
| Чому дорівнює середня квадратична похибка різниці двох вимірів, якщо середня квадратична похибка одного виміру m=1,4мм.
| Р.1:П.6
|
|
| а) 1 мм
б) 2 мм
в) 5 мм
г) 9 мм
д) 0 мм
|
|
| 6.
| Виміряні дві лінії: одна довжиною 100м з середньою квадратичною похибкою 3см, друга – 150м з середньою квадратичною похибкою 4см. З якою точністю обчислюватимуться віддалі, що рівні різниці двох ліній?
| Р.1:П.6
|
|
| а) 1 см
б) 2 см
в) 3 см
г) 5 см
д) 0 cм
|
|
| 7.
| Обчислити нев’язку в сумі кутів трикутника, якщо середні квадратичні похибки кожного кута дорівнюють: mα=5"; mβ=4"; mγ=3";.
| Р.1:П.6
|
|
| а) 1"
б) 5"
в) 7"
г) 10"
д) 0"
|
|
| 8.
| Виміряні лінії l1=175м; l2=205м з середньою квадратичною похибкою ml=5мм. З якою тонічністю обчислюватимуться лінії l1 + l2 ?
| Р.1:П.6
|
|
| а) 10 мм
б) 9 мм
в) 15 мм
г) 7 мм
д) 0 мм
|
|
| 9.
| Кути α; та β; трикутника виміряні з середніми квадратичними похибками mα=6";; mβ=8";. Знайти середню квадратичну похибку третього кута γ.
| Р.1:П.6
|
|
| а) 1"
б) 10"
в) 5"
г) 3"
д) 0"
|
|
| 10.
| Виміряні лінії l1=270м; l2=300м з середньою квадратичною похибкою ml=5мм. З якою тонічністю обчислюватимуться лінії l2 – l1 ?
| Р.1:П.6
|
|
| а) 10 мм
б) 7 мм
в) 18 мм
г) 0 мм
д) 20 мм
|
|
| 11.
| Визначити середню квадратичну похибку в сумі кутів трикутника, якщо mα=mβ=1,0"; mγ=1,4";.
| Р.1:П.6
|
|
| а) 5"
б) 7"
в) 2"
г) 10"
д) 0"
|
|
| 12.
| Оцінити точність функції U=x+y+z, якщо mx=1,0мм; my=1,1мм; mz=1,3мм.
| Р.1:П.6
|
|
| а) 2 мм
б) 5 мм
в) 10 мм
г) 15 мм
д) 0 мм
|
|
| 13.
| Вага суми кутів шестикутника прийнята за одиницю. Визначити вагу одного кута.
| Р.1:П.10
|
|
| а) 1
б) 4
в) 6
г) 10
д) 0
|
|
| 14.
| Загальна площа ділянки складається з 5-ти частин, що вимірюються на плані з однаковою точністю планіметром. Вага всієї площі Р∑=0,2. Знайти вагу однієї частини площі.
| Р.1:П.10
|
|
| а) 1
б) 3
в) 5
г) 9
д) 0
|
|
| 15.
| У трикутнику один кут виміряний з вагою 3, другий – 6. Визначити вагу кута, який визначається через два перших.
| Р.1:П.10
|
|
| а) 1
б) 2
в) 5
г) 10
д) 0
|
|
| 16.
| Вага суми кутів п’ятикутника, виміряних з однаковою точністю, прийнята за одиницю. Знайти вагу одного кута.
| Р.1:П.10
|
|
| а) 1
б) 9
в) 3
г) 5
д) 0
|
|
| 17.
| Кут отриманий як різниця двох рівноточних напрямків. Знайти вагу напрямку, прийнявши вагу кута рівною одиниці.
| Р.1:П.10
|
|
| а) 1
б) 9
в) 2
г) 4
д) 0
|
|
| 18.
| Кут знаходиться як різниця двох рівноточних напрямків. Знайти вагу напрямку, прийнявши вагу кута рівною 8.
| Р.1:П.10
|
|
| а) 16
б) 20
в) 10
г) 26
д) 0
|
|
| 19.
| Обчислити вагу Рγ кута γ=α+β;, якщо ваги кутів α; та β; дорівнюють відповідно 3 та 15.
| Р.1:П.10
|
|
| а) 0,5
б) 1,5
в) 4,5
г) 2,5
д) 0
|
|
| 20.
| Значення кута отримане як середнє з n=16 прийомів і має середню квадратичну похибку М=2,5";. Знайти середню квадратичну похибку кута, виміряного одним прийомом.
| Р.1:П.6
|
|
| а) 10"
б) 5"
в) 15"
г) 20"
д) 0"
|
|
| 21.
| Знайти середню квадратичну похибку одного кута у полігоні з 16-ма кутами, якщо середня квадратична похибка суми всіх кутів дорівнює 2,0";.
| Р.1:П.6
|
|
| а) 0"
б) 1,5"
в) 0,5"
г) 2,5"
д) 1"
|
|
| 22.
| Середня квадратична похибка суми кутів дев’ятикутника рівна m∑=15";. Визначити середню квадратичну похибку одного кута.
| Р.1:П.6
|
|
| а) 1"
б) 5"
в) 3"
г) 10"
д) 0"
|
|
| 23.
| Середня квадратична похибка середнього арифметичного, знайденого з 4-х прийомів виміру кута, дорівнює 0,8";. Знайти середню квадратичну похибку одного виміру.
| Р.1:П.6
|
|
| а) 0,6"
б) 3,6"
в) 7,6"
г) 1,6"
д) 0"
|
|
| 24.
| Чому дорівнює середня квадратична похибка одного виміру, якщо середня квадратична похибка різниці двох вимірів ml=1,41мм.
| Р.1:П.6
|
|
| а) 10 мм
б) 5 мм
в) 1 мм
г) 0 мм
д) 20 мм
|
|
| 25.
| В замкненому полігоні виміряні 9 кутів. Чому дорівнює середня квадратична похибка одного кута, якщо середня квадратична похибка кутової нев’язки полігона рівна mf =15";.
| Р.1:П.6
|
|
| а) 1"
б) 3"
в) 9"
г) 5"
д) 0"
|
|
| 26.
| Середня квадратична похибка кута, знайденого з 16 прийомів, дорівнює 2";. Знайти середню квадратичну похибку кута, виміряного одним прийомом.
| Р.1:П.6
|
|
| а) 16"
б) 8"
в) 2"
г) 32"
д) 0"
|
|
| 27.
| Середня квадратична похибка суми кутів чотирикутника, виміряних з однаковою точністю, рівна m∑=8,0";. Знайти середню квадратичну похибку одного кута.
| Р.1:П.6
|
|
| а) 9"
б) 7"
в) 4"
г) 1"
д) 0"
|
|
| 28.
| Знайти середню квадратичну похибку одного кута в полігоні з 16-ма кутами, якщо середня квадратична похибка суми всіх кутів дорівнює m∑=2,0";.
| Р.1:П.6
|
|
| а) 0,5"
б) 2,5"
в) 3,5"
г) 5,5"
д) 0"
|
|
| 29.
| Cередня похибка ряду рівноточних вимірів дорівнює 4";. Чому дорівнює середня квадратична похибка остаточного значення вимірюваної величини?
| Р.1:П.5
|
|
| а) 5"
б) 10"
в) 20"
г) 2"
д) 0"
|
|
| 30.
| З ряду рівноточних вимірів знайдена середня похибка 16мм. Чому дорівнює середня квадратична похибка?
| Р.1:П.5
|
|
| а) 50 мм
б) 30 мм
в) 20 мм
г) 10 мм
д) 0 мм
|
|
| 31.
| Ймовірна похибка ряду рівноточних вимірів дорівнює 2";. Чому дорівнює середня квадратична похибка остаточного значення вимірюваної величини?
| Р.1:П.5
|
|
| а) 1"
б) 3"
в) 5"
г) 10"
д) 0"
|
|
| 32.
| З ряду рівноточних вимірів знайдена середня квадратична похибка 8мм. Чому дорівнює ймовірна похибка?
| Р.1:П.5
|
|
| а) 5 мм
б) 3 мм
в) 10 мм
г) 7 мм
д) 0 мм
|
|
| 33.
| Середня квадратична похибка одного виміру кута m=0,5";; вага р=4. Чому дорівнює середня квадратична похибка одиниці ваги?
| Р.1:П.9
|
|
| а) 3"
б) 1"
в) 5"
г) 9"
д) 0"
|
|
| 34.
| Вага кута дорівнює 9. Знайти середню квадратичну похибку цього кута, якщо середня квадратична похибка одиниці ваги µ=15";.
| Р.1:П.9
|
|
| а) 3"
б) 1"
в) 9"
г) 5"
д) 0"
|
|
| 35.
| Середня квадратична похибка одиниці ваги µ=16";; вага р=16. Чому дорівнює середня квадратична похибка одного виміру кута?
| Р.1:П.9
|
|
| а) 4"
б) 2"
в) 8"
г) 10"
д) 0"
|
|
| 36.
| Середня квадратична похибка кута дорівнює 3";. Знайти вагу цього кута, якщо середня квадратична похибка одиниці ваги µ=6";.
| Р.1:П.9
|
|
| а) 1
б) 2
в) 4
г) 10
д) 0
|
|
| 37.
| Середня квадратична похибка виміру перевищення m=2мм; вага р=25. Чому дорівнює середня квадратична похибка одиниці ваги?
| Р.1:П.9
|
|
| а) 20 мм
б) 30 мм
в) 10 мм
г) 1 мм
д) 0 мм
|
|
| 38.
| Вага перевищення дорівнює 4. Знайти середню квадратичну похибку цього перевищення, якщо середня квадратична похибка одиниці ваги µ=20мм.
| Р.1:П.9
|
|
| а) 1 мм
б) 15 мм
в) 30 мм
г) 10 мм
д) 0 мм
|
|
| 39.
| Середня квадратична похибка довжини лінії дорівнює 3мм. Знайти її вагу, якщо середня квадратична похибка одиниці ваги µ=12мм.
| Р.1:П.9
|
|
| а) 10
б) 16
в) 20
г) 26
д) 0
|
|
| 40.
| Середня квадратична похибка кута дорівнює 2 ";. Знайти вагу цього кута, якщо середня квадратична похибка одиниці ваги µ=4";.
| Р.1:П.9
|
|
| а) 1
б) 8
в) 9
г) 4
д) 0
|
|
| 41.
| За вибіркою обсягу n=10 знайдено зміщену оцінку 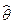 =9 для дисперсії генеральної сукупності. Знайти її незміщену оцінку. =9 для дисперсії генеральної сукупності. Знайти її незміщену оцінку.
| Р.3:П.3
|
|
| а) 9
б) 1
в) 10
г) 0
д) 90
|
|
| 42.
| Для вибірки обсягу n=4 знайдено незміщену оцінку 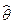 =80 дисперсії генеральної сукупності. Знайти її зміщену оцінку. =80 дисперсії генеральної сукупності. Знайти її зміщену оцінку.
| Р.3:П.3
|
|
| а) 60
б) 80
в) 40
г) 100
д) 0
|
|
| 43.
| За вибіркою обсягу n=6 знайдено незміщену оцінку 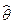 =60 для дисперсії генеральної сукупності. Знайти її зміщену оцінку. =60 для дисперсії генеральної сукупності. Знайти її зміщену оцінку.
| Р.3:П.3
|
|
| а) 60
б) 6
в) 50
г) 80
д) 0
|
|
| 44.
| Для вибірки обсягу n=5 знайдено зміщену оцінку 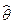 =20 дисперсії генеральної сукупності. Знайти її незміщену оцінку. =20 дисперсії генеральної сукупності. Знайти її незміщену оцінку.
| Р.3:П.3
|
|
| а) 20
б) 5
в) 25
г) 35
д) 0
|
|
| 45.
| За вибіркою обсягу n=3 знайдено незміщену оцінку 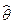 =15 для дисперсії генеральної сукупності. Знайти її зміщену оцінку. =15 для дисперсії генеральної сукупності. Знайти її зміщену оцінку.
| Р.3:П.3
|
|
| а) 10
б) 15
в) 3
г) 25
д) 0
|
|
| 46.
| Для вибірки обсягу n=2 знайдено зміщену оцінку 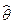 =10 дисперсії генеральної сукупності. Знайти її незміщену оцінку. =10 дисперсії генеральної сукупності. Знайти її незміщену оцінку.
| Р.3:П.3
|
|
| а) 10
б) 15
в) 20
г) 25
д) 0
|
|
| 47.
| За вибіркою обсягу n=4 знайдено незміщену оцінку 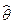 =8 для дисперсії генеральної сукупності. Знайти її зміщену оцінку. =8 для дисперсії генеральної сукупності. Знайти її зміщену оцінку.
| Р.3:П.3
|
|
| а) 8
б) 6
в) 4
г) 0
д) 1
|
|
| 48.
| Для вибірки обсягу n=7 знайдено зміщену оцінку 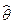 =18 дисперсії генеральної сукупності. Знайти її незміщену оцінку. =18 дисперсії генеральної сукупності. Знайти її незміщену оцінку.
| Р.3:П.3
|
|
| а) 21
б) 18
в) 7
г) 30
д) 0
|
|
| 49.
| За вибіркою обсягу n=3 знайдено незміщену оцінку 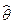 =45 для дисперсії генеральної сукупності. Знайти її зміщену оцінку. =45 для дисперсії генеральної сукупності. Знайти її зміщену оцінку.
| Р.3:П.3
|
|
| а) 45
б) 3
в) 60
г) 30
д) 0
|
|
| 50.
| Для вибірки обсягу n=8 знайдено зміщену оцінку 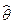 =70 дисперсії генеральної сукупності. Знайти її незміщену оцінку. =70 дисперсії генеральної сукупності. Знайти її незміщену оцінку.
| Р.3:П.3
|
|
| а) 70
б) 8
в) 80
г) 90
д) 0
|
|
| 51.
| Обчислити середню квадратичну похибку першого невідомого для оцінки точності результатів зрівноважування параметричним методом, якщо [pvv]=36, кількість вимірів n=12, кількість невідомих k=3, а обернена матриця Q коефіцієнтів нормальних рівнянь має вигляд:
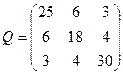
| Р.4:П.5
|
|
| а) 5
б) 10
в) 7
г) 2
д) 0
|
|
| 52.
| Обчислити середню квадратичну похибку другого невідомого для оцінки точності результатів зрівноважування параметричним методом, якщо [pvv]=64, кількість вимірів n=7, кількість невідомих k=3, а обернена матриця Q коефіцієнтів нормальних рівнянь має вигляд:
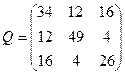
| Р.4:П.5
|
|
| а) 28
б) 18
в) 8
г) 2
д) 0
|
|
| 53.
| Обчислити середню квадратичну похибку третього невідомого для оцінки точності результатів зрівноважування параметричним методом, якщо [pvv]=100, кількість вимірів n=28, кількість невідомих k=3, а обернена матриця Q коефіцієнтів нормальних рівнянь має вигляд:
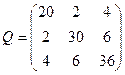
| Р.4:П.5
|
|
| а) 2
б) 22
в) 10
г) 12
д) 0
|
|
| 54.
| Обчислити середню квадратичну похибку першого невідомого для оцінки точності результатів зрівноважування параметричним методом, якщо [pvv]=16, кількість вимірів n=19, кількість невідомих k=3, а обернена матриця Q коефіцієнтів нормальних рівнянь має вигляд:

| Р.4:П.5
|
|
| а) 2
б) 6
в) 4
г) 8
д) 0
|
|
| 55.
| Обчислити середню квадратичну похибку другого невідомого для оцінки точності результатів зрівноважування параметричним методом, якщо [pvv]=36, кількість вимірів n=7, кількість невідомих k=3, а обернена матриця Q коефіцієнтів нормальних рівнянь має вигляд:
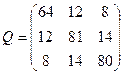
| Р.4:П.5
|
|
| а) 27
б) 17
в) 7
г) 1
д) 0
|
|
| 56.
| Обчислити середню квадратичну похибку третього невідомого для оцінки точності результатів зрівноважування параметричним методом, якщо [pvv]=81, кількість вимірів n=12, кількість невідомих k=3, а обернена матриця Q коефіцієнтів нормальних рівнянь має вигляд:

| Р.4:П.5
|
|
| а) 16
б) 2
в) 6
г) 8
д) 0
|
|
| 57.
| Обчислити середню квадратичну похибку першого невідомого для оцінки точності результатів зрівноважування параметричним методом, якщо [pvv]=64, кількість вимірів n=19, кількість невідомих k=3, а обернена матриця Q коефіцієнтів нормальних рівнянь має вигляд:
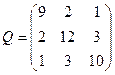
| Р.4:П.5
|
|
| а) 16
б) 6
в) 10
г) 4
д) 0
|
|
| 58.
| Обчислити середню квадратичну похибку другого невідомого для оцінки точності результатів зрівноважування параметричним методом, якщо [pvv]=36, кількість вимірів n=28, кількість невідомих k=3, а обернена матриця Q коефіцієнтів нормальних рівнянь має вигляд:
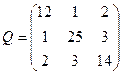
| Р.4:П.5
|
|
| а) 2
б) 5
в) 4
г) 6
д) 0
|
|
| 59.
| Обчислити середню квадратичну похибку третього невідомого для оцінки точності результатів зрівноважування параметричним методом, якщо [pvv]=49, кількість вимірів n=67, кількість невідомих k=3, а обернена матриця Q коефіцієнтів нормальних рівнянь має вигляд:
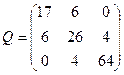
| Р.4:П.5
|
|
| а) 5
б) 7
в) 9
г) 3
д) 0
|
|
| 60.
| Обчислити середню квадратичну похибку першого невідомого для оцінки точності результатів зрівноважування параметричним методом, якщо [pvv]=16, кількість вимірів n=12, кількість невідомих k=3, а обернена матриця Q коефіцієнтів нормальних рівнянь має вигляд:
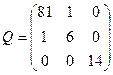
| Р.4:П.5
|
|
| а) 12
б) 22
в) 10
г) 2
д) 0
|
|
| 61.
| Обчислити середню квадратичну похибку першого невідомого для оцінки точності результатів зрівноважування параметричним методом, якщо середня квадратична похибка одиниці ваги µ=7, а обернена матриця Q коефіцієнтів нормальних рівнянь має вигляд:
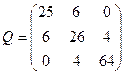
| Р.4:П.5
|
|
| а) 25
б) 35
в) 15
г) 5
д) 0
|
|
| 62.
| Обчислити середню квадратичну похибку другого невідомого для оцінки точності результатів зрівноважування параметричним методом, якщо середня квадратична похибка одиниці ваги µ=4, а обернена матриця Q коефіцієнтів нормальних рівнянь має вигляд:
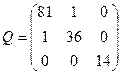
| Р.4:П.5
|
|
| а) 4
б) 14
в) 34
г) 24
д) 0
|
|
| 63.
| Обчислити середню квадратичну похибку третього невідомого для оцінки точності результатів зрівноважування параметричним методом, якщо середня квадратична похибка одиниці ваги µ=3,5, а обернена матриця Q коефіцієнтів нормальних рівнянь має вигляд:
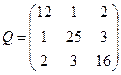
| Р.4:П.5
|
|
| а) 14
б) 4
в) 24
г) 10
д) 0
|
|
| 64.
| Обчислити середню квадратичну похибку першого невідомого для оцінки точності результатів зрівноважування параметричним методом, якщо середня квадратична похибка одиниці ваги µ=2/3, а обернена матриця Q коефіцієнтів нормальних рівнянь має вигляд:

| Р.4:П.5
|
|
| а) 8
б) 6
в) 4
г) 2
д) 0
|
|
| 65.
| Обчислити середню квадратичну похибку другого невідомого для оцінки точності результатів зрівноважування параметричним методом, якщо середня квадратична похибка одиниці ваги µ=4/9, а обернена матриця Q коефіцієнтів нормальних рівнянь має вигляд:
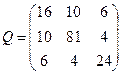
| Р.4:П.5
|
|
| а) 8
б) 6
в) 4
г) 2
д) 0
|
|
| 66.
| Для вимірюваних величин x, y, z, u складено параметричні рівняння:
x= t1 – t2; y=2t1 – 3t2 – 2; z=t1+t2; u=5t1+4t2+3.
Скільки буде умовних рівнянь?
| Р.4:П.9
|
|
| а) 2
б) 6
в) 3
г) 4
д) 0
|
|
| 67.
| Для вимірюваних величин у1, у2, у3 складено параметричні рівняння:
y1=t1+2; y2=3t1 – 3; y3= – t1+4.
Скільки буде умовних рівнянь?
| Р.4:П.9
|
|
| а) 4
б) 1
в) 3
г) 2
д) 0
|
|
| 68.
| Для вимірюваних величин x, y, z, u параметричні рівняння мають вигляд:
x=2t1+3t2; y= – t1+5t2+1; z=t1; u=t1 – t2.
Скільки буде умовних рівнянь?
| Р.4:П.9
|
|
| а) 1
б) 2
в) 3
г) 4
д) 0
|
|
| 69.
| Для вимірюваних величин х1, х2, х3, х4 складено параметричні рівняння:
х1=t1 – t2+2; x2=2t1+t2 – 3;
x3= – t1+t2 – 3; x4=3t1+4t2.
Скільки буде умовних рівнянь?
| Р.4:П.9
|
|
| а) 4
б) 6
в) 2
г) 1
д) 0
|
|
| 70.
| Для вимірюваних величин x,y,z складено параметричні рівняння:
x= – t1+t2+2; y=3t1 – 4t2; z= – t1+2t2 – 1.
Скільки буде умовних рівнянь?
| Р.4:П.9
|
|
| а) 1
б) 5
в) 3
г) 4
д) 0
|
|
| 71.
| Для вимірюваних величин x, y, z складено параметричні рівняння:
х=2t1 – 14; y= – t2+2; z=t1+t2.
Скільки буде умовних рівнянь?
| Р.4:П.9
|
|
| а) 5
б) 1
в) 3
г) 2
д) 0
|
|
| 72.
| Для вимірюваних величин х1, х2, х3, х4 складено параметричні рівняння:
x1=t1 – 2t2+3t3; x2=2t1+t2 – 2t3;
x3=t1 – t2 – t3; x4= – t1 – t2 – 3t3.
Скільки буде умовних рівнянь?
| Р.4:П.9
|
|
| а) 4
б) 7
в) 3
г) 1
д) 0
|
|
| 73.
| Для вимірювання величин x, y складено параметричні рівняння:
x=2t1+2; y= – t1+4.
Скільки виникає умовних рівнянь?
| Р.4:П.9
|
|
| а) 3
б) 4
в) 1
г) 2
д) 0
|
|
| 74.
| Для вимірюваних величин x, y, z складено параметричні рівняння:
x=t1; y=t1 – 2t2; z=2t1+6t2+3.
Скільки буде умовних рівнянь?
| Р.4:П.9
|
|
| а) 1
б) 2
в) 3
г) 5
д) 0
|
|
| 75.
| Для виміряних величин x, y, z складено параметричні рівняння:
x=t1+t2 – 3; y= – 2t1+3t2+4; z=6t1+t2+6.
Скільки буде умовних рівнянь?
| Р.4:П.9
|
|
| а) 3
б) 1
в) 5
г) 2
д) 0
|
|
| 76.
| Для вимірюваних величин x, y, z, u параметричні рівняння мають вигляд:
x=2t1+3t2; y=4t1+5t2+1; z=t1; u=8t1+3t2.
Скільки буде умовних рівнянь?
| Р.4:П.9
|
|
| а) 2
б) 4
в) 6
г) 3
д) 0
|
|
| 77.
| Для вимірюваних величин х1, х2, х3 параметричні рівняння мають вигляд:
x1=2t1+3t2+1; x2=t1+t2+4; x3=5t2.
Скільки буде умовних рівнянь?
| Р.4:П.9
|
|
| а) 5
б) 3
в) 2
г) 1
д) 0
|
|
| 78.
| Для вимірюваних величин x,y,z складено параметричні рівняння:
x=t1+2t2+2; y=3t1+4t2; z=t1+2t2+1.
Скільки буде умовних рівнянь?
| Р.4:П.9
|
|
| а) 2
б) 1
в) 3
г) 5
д) 0
|
|
| 79.
| Для виміряних величин x, y, z складено параметричні рівняння:
x=5t1+4t2+3; y=2t1+3t2+4; z=6t1+t2+6.
Скільки буде умовних рівнянь?
| Р.4:П.9
|
|
| а) 5
б) 3
в) 1
г) 2
д) 0
|
|
| 80.
| Для вимірюваних величин x, y, z складено параметричні рівняння:
x=7t1; y=3t1+2t2; z=2t1+6t2+3.
Скільки буде умовних рівнянь?
| Р.4:П.9
|
|
| а) 5
б) 3
в) 2
г) 1
д) 0
|
|