Погрешности вычислений1. Неадекватность выбранной математической модели исходной физической. Эта неадекватность в большей или меньшей степени присуща всем приближенно решаемым задачам. Данная погрешность является неустранимой, и она определяется апостериорным путем (на шестом этапе решения задачи. Остальные три типа погрешностей являются сугубо вычислительными и обусловлены следующими причинами. 2. Неустранимые погрешности Связаны с точностью измерений или вычислений, или округлением исходных данных данных. 3. Погрешность численного или какого-либо другого приближенного метода Если неопределенность в исходных данных каким-либо образом устранена, и решение найдено с помощью какого-либо численного метода, то результат не будет в точности соответствовать исходным данным. Это и есть погрешность численного метода. Именно такие погрешности будут оцениваться при рассмотрении численных методов. Эти оценки могут получаться до выполнения вычислений (априорные оценки) и после них (апостериорные оценки). 4. Ошибки округления В компьютере все числа представляются в конечном виде, и поэтому при использовании вычислительного алгоритма возникают ошибки арифметических и других операций над числами − ошибки округления.
Погрешность действий над приближенными величинами Пусть х — точное, но, как правило, неизвестное значение величины, а Абсолютной погрешностью приближения Относительная погрешность приближения Так как величина х, как правило, неизвестна, а погрешность необходимо определять, то в рассмотрение вводится предельная абсолютная погрешность Δ(
Раскрывая в этом неравенстве модуль, получаем соотношение, задающее отрезок, которому принадлежит точное значение: Таким образом, величина х находится в Δ-окрестности (дельта-окрестности), определяемой величинами Предельная относительная погрешность приближения
Значащими цифрами приближенного числа называют все цифры в его записи, начиная с первой ненулевой слева. Первые п значащих цифр приближенного числа называются верными, если абсолютная погрешность этого числа не превышает половины единицы разряда, соответствующего n -й значащей цифре, считая слева направо. Вычислить приближенное число с точностью ε = 10- n означает, что необходимо сохранить верной значащую цифру, стоящую в n -м разряде после запятой. На практике возникает надобность в округлении приближенного числа, т.е. замене его числом с меньшим количеством значащих цифр. Для округления числа до п значащих цифр следует отбросить все его цифры, стоящие справа от n -й значащей цифры. Рассмотрим правило вычисления погрешностей арифметических операций и функций по погрешности аргументов (без учета ошибок округления). При вычислении абсолютных погрешностей обычно используются формулы дифференцирования, в которых дифференциалы независимых переменных заменяются абсолютными погрешностями (dхi = Δ; Пусть x1 > 0, х2 > 0 и заданы предельные абсолютные погрешности Δ( Так как dx = dx1 + dx2, то
Теперь предположим, что x1 >х2, и найдем погрешность разности х =х,-х2. Тогда dx=dx1- dx2 и
Таким образом, абсолютная погрешность суммы и разности двух приближенных чисел равна сумме абсолютных погрешностей слагаемых. Это правило справедливо для произвольного числа слагаемых. Так, если
Для относительной погрешности суммы и разности двух чисел х1 ± х2 получаем
Для произвольного числа слагаемых
где Пусть
Поэтому Аналогично при выполнении умножения и деления получаем погрешности (при тех же предположениях):
Изпоследних соотношений следует, что относительная погрешность произведения двух чисел равна сумме относительных погрешностей его сомножителей. Аналогичное правило выполняется и для частного от деления двух чисел. Замечание. При вычитании близких чисел на ЭВМ происходит потеря верных значащих цифр, поскольку разность Пример Требуется вычислить разность у = х 1 - х 2 двух близких чисел х 1 = 0,0 1234 и х 2 =0,0 1231, для которых □ Величина у = х1 - х2 = 0,00003 имеет только одну значащую цифру, так как D(ŷ) = 0,000004 < 0,5*10-5 Аналогично получаются формулы для погрешностей арифметических действий при вычислении функций многих переменных. Так, для z = f(x 1 ,x 2 i...,xn) имеем следующие формулы для погрешностей:
В арифметике целых чисел на ЭВМ операции сложения, вычитания и умножения выполняются точно. Деление целых чисел осуществляется с округлением — заменой частного его целой частью. Если в вычислениях присутствует большое число операций деления, то в целочисленной арифметике это может привести к большой погрешности из-за ошибок округления. В арифметике вещественных чисел на ЭВМ все четыре действия, как правило, выполняются с округлением. Исключение составляют действия над числами, которые не выходят за разрядность ЭВМ. Оценка погрешностей округлений при решении многих задач на ЭВМ может быть найдена апостериорным путем с помощью двух повторных расчетов в арифметике одинарной и двойной точности и составления разности полученных результатов. Этот прием используется также и для оценки погрешностей численного метода (модели).
|


 — ее известное приближенное значение.
— ее известное приближенное значение. (δ-безразмерная величина,
(δ-безразмерная величина, 
 . Отсюда получается часто используемое соотношение
. Отсюда получается часто используемое соотношение
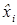 ,).
,). ), Δ(
), Δ(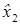 ), т.е. x 1 =
), т.е. x 1 =  . Отсюда следует, что
. Отсюда следует, что .
. , поэтому
, поэтому
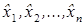 имеют одну и ту же погрешность
имеют одну и ту же погрешность  , то
, то 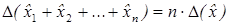 Но реально погрешности могут иметь разные знаки и потому взаимно компенсировать друг друга. По правилу Чеботарева при п > 10 можно принять
Но реально погрешности могут иметь разные знаки и потому взаимно компенсировать друг друга. По правилу Чеботарева при п > 10 можно принять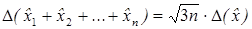 .
.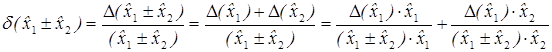

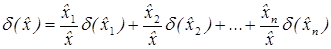
 ;
; 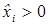 , i=1,…,n.
, i=1,…,n.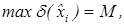
 тогда
тогда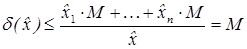 ,
, 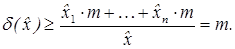

 ,
, 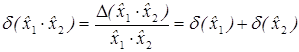 ,)
,) ,)
,)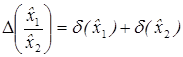
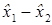 близка к нулю и, следовательно, относительная погрешность разности значительно больше относительной погрешности уменьшаемого и вычитаемого.
близка к нулю и, следовательно, относительная погрешность разности значительно больше относительной погрешности уменьшаемого и вычитаемого. (абсолютная погрешность результата удвоилась). Таким образом, произошла потеря трех верных значащих цифр. Это следует учитывать при составлении алгоритма, по возможности избегая потери точности с помощью алгебраических преобразований формулы и изменения в ней последовательности вычислений.
(абсолютная погрешность результата удвоилась). Таким образом, произошла потеря трех верных значащих цифр. Это следует учитывать при составлении алгоритма, по возможности избегая потери точности с помощью алгебраических преобразований формулы и изменения в ней последовательности вычислений.
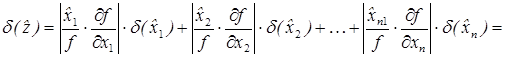 (А.15)
(А.15)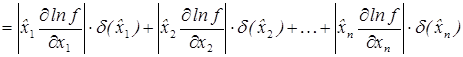 .
.


