Дифференциальные уравнения пограничного слоя.При обтекании твердой поверхности жидкостью (или газом) с большими числами Re влияние вязкости проявляется в пределах тонкого пограничного слоя δ (рис. 7.1.) Вне этого слоя во многих задачах среда может полагаться невязкой и ее течение описывается системой уравнений Эйлера. Л. Прандтль установил, что в пределах тонкого пограничного слоя уравнения вязкой среды могут быть существенно упрощены в предположении о сопоставимости сил вязкости и инерции. Если между поверхностью обтекаемого тела и жидкостью происходит тепло и массообмен то вблизи твердой стенки возникают тепловой и диффузионный пограничные слои толщиной δт и δс. Скорость, температура и концентрация примеси принимают у стенки значения Uст, Тст и Сст и асимптотически приближаются к значениям U
Рис. 7.1. Схема динамического, теплового и концентрационного пограничных слоев на криволинейной поверхности 4.10.1. Система уравнений вязкой жидкости рассматривается при следующих допущениях: течение двумерное, среда однофазная, внешние объемные силы отсутствуют. При этих допущениях система уравнений Навье-Стокса имеет вид: - уравнение неразрывности
1 1∙1 - уравнение движения в проекции на ось х
1 1 - уравнение движения в проекции на ось у
1 1 - уравнение баланса энергии
1 1 где Ф – диссипативная функция
где под каждым слагаемым записаны порядки величин, которые необходимо оценить. Будем считать, что толщины δ и δт имеют порядок δ значительно меньший по сравнению с расстоянием х. Порядок х, а, Uх, Т, ρ, р – примем за 1. Тогда δ << х. Оценим порядки слагаемых в уравнениях (7.1) – (7.4) и разместим эти порядки под соответствующими величинами. В уравнении неразрывности слагаемое Таким образом, оставляя в уравнениях слагаемые, имеющие большие порядки, а именно в (7.2) порядка 1, в (7.3) порядка - уравнение неразрывности
- уравнение движения в проекции на ось х
- уравнение движения в проекции на ось у
- уравнение баланса энергии
Замыкающим уравнением является уравнение состояния ρ = ρ (р,Т) (7.9) Система уравнений (7.5) – (7.9) содержащее 5 неизвестных ρ (х, у), Ux (х, у), Uy (х, у), р (х, у), Т (х, у) является замкнутой при известных μ(т), λ(т), Ср(т) и относится к системам уравнений параболического типа. Граничные условия в задачах расчета пограничных слоев задаются в следующем виде: - в сечении при входе на рассматриваемый участок пограничного слоя задаются профили продольной скорости и температуры при х = 0, Ux = Ux0(y), Т =Т0(у), а также профиль поперечной скорости у = Uу0(y), удовлетворяющий уравнению неразрывности. - на твердой стенке при у = 0, Ux = Uxст(х), Uу = Uуст(х), Т =Тст(х), в частном случае условий «прилипания» жидкости на стенке Uxст = Uуст = 0 - на внешней границе пограничного слоя у→ ∞ (у >δ, у >δт), р = р∞(х), Т = Т∞(х) Скорость потока на внешней границе пограничного слоя находится из уравнения Бернулли для газа
где К – показатель адиабаты газа. Система уравнений (7.5) – (7.9) с выписанными граничными условиями решается численно стандартным методом конечных разностей, методом контрольных объемов и другими. Для несжимаемой жидкости плотность ρ = ρ0 = соnst и система уравнений пограничного слоя (7.4) – (7.8) упрощается:
- уравнение движения в проекции на ось х
- уравнение движения в проекции на ось у
- уравнение энергии
Для калорически совершенного (идеального) газа уравнение состояния
и удельная энтальпия i равна i = CpT Полагая удельную массовую изобарную теплоемкость Ср постоянной, умножая (7.6) и складывая почленно результат с (7.8) получим уравнение энергии в форме Широкова
где
|

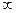 , Т
, Т 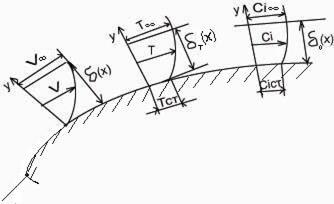
 (7.1)
(7.1)
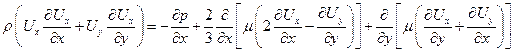 (7.2)
(7.2) δ
δ 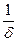
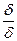
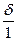
 (7.3)
(7.3) (7.4)
(7.4) ,
,
 ~
~  то есть имеет порядок 1 и, следовательно,
то есть имеет порядок 1 и, следовательно,  ~1 и т.к. у ~ δ, то Uу ~ δ. Производные
~1 и т.к. у ~ δ, то Uу ~ δ. Производные 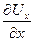 ~ 1 и
~ 1 и 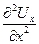 ~ 1, т.е. имеют порядок 1, а производные
~ 1, т.е. имеют порядок 1, а производные 
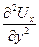 имеют порядки
имеют порядки 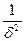 соответственно. Полагая, что силы вязкости и инерции имеют в пределах пограничного слоя одинаковый порядок получим из (7.2) 1 ~
соответственно. Полагая, что силы вязкости и инерции имеют в пределах пограничного слоя одинаковый порядок получим из (7.2) 1 ~  и μ ~
и μ ~ 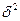 . Тогда число
. Тогда число 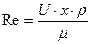 ~
~  ~
~ 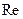 . В уравнении энергии (7.4) полагаем, что тепловые потоки из-за теплопроводности имеют такой же порядок что и конвективный тепловой поток. Тогда слагаемое
. В уравнении энергии (7.4) полагаем, что тепловые потоки из-за теплопроводности имеют такой же порядок что и конвективный тепловой поток. Тогда слагаемое 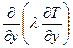 имеет порядок 1 и, следовательно, λ имеет порядок δ2.
имеет порядок 1 и, следовательно, λ имеет порядок δ2.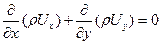 (7.5)
(7.5) (7.6)
(7.6) (7.7)
(7.7)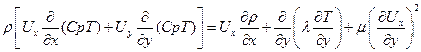 (7.8)
(7.8)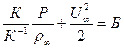 , (7.10)
, (7.10) (7.11)
(7.11)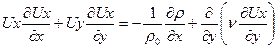 (7.12)
(7.12)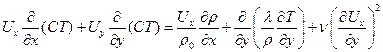 (7.14)
(7.14)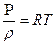 (7.15)
(7.15)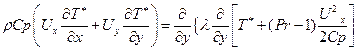 (7.16)
(7.16)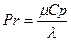 - число Прандтля
- число Прандтля 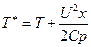 - температура адиабатического λ по скорости Ux.
- температура адиабатического λ по скорости Ux.


