Нахождение собственных векторов и собственных значенийОпределение. Вектор
где Нахождение собственных векторов и собственных значений сводится к решению уравнения:
которое в свою очередь сводится к:
Теорема. Пусть собственные значения Следствие. Если характеристический многочлен оператора Пример 1. Найти собственные вектора и собственные значения матрицы
Заметим, что матрица Решение: Собственные вектора – это такие вектора, при которых Найдем собственные значения
Найдем собственные вектора для каждого собственного значения:
Получаем:
Пронормируем этот вектор:
Получаем собственные вектора для данного собственного значения:
Пронормируем:
Ответ: Cобственные значения матрицы:
собственные вектора:
Пример 2. Привести матрицу к диагональному виду:
Решение:
Раскроем скобки, приведем подобные слагаемые:
Подбором найдем корень
Для каждого собственного значения необходимо найти собственный вектор:
Получим систему уравнений, из которой найдем собственный вектор:
где
Методом подбора можно получить множество различных векторов. По теореме, собственные векторы линейно независимы, если собственные значения оператора
Тогда получим два собственных вектора при собственном значении
Таким образом, собственные векторы оператора
Ортонормированная система собственных векторов:
Матрица
Для приведения матрицы
необходимо найти матрицу, обратную матрице
Для матрицы
Итак, матрица
Упражнение. Найти собственные вектора, собственные значения матрицы
Решение. Матрица симметричная, поэтому она диагонализируема. Найдем собственные значения
Найдем собственные векторы для данных собственных значений:
Получаем:
где Пронормируем этот вектор:
Получаем собственные вектора для данного собственного значения:
Пронормируем:
Таким образом, собственные векторы оператора
Ортонормированная система собственных векторов:
Матрица
Для приведения матрицы
необходимо найти матрицу, обратную матрице
Для матрицы
Итак, матрица
Интерпретация понятия «собственный вектор» (автор — Маресов А.Г., выпускник физфака МГУ, сотрудник аналитического центра «Газпромбанка»). Любое уравнение физики связано операторами через собственные вектора: Пример 1. При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости. Простейшим видом деформации является деформация растяжения (Рис. 1 и Рис. 2)
Внешняя сила, действующая на пружину и растягивающая ее равна:
При малых деформациях (
По II закону Ньютона, сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение,
Ускорение — есть вторая производная по времени от расстояния (изменения координаты):
В физике введено обозначение
Тогда формула упрощается:
Таким образом оператор второй производной по времени так действует на
Пример 2. Оптика. Отражение и преломление На границе раздела двух прозрачных сред свет может частично отразиться так, что часть световой энергии будет распространяться после отражения по новому направлению, а частично пройти через границу и распространяться во второй среде. Закон отражения света: Угол отражения Закон преломления: Отношение синуса угла падения
Рассмотрим упрощенный случай: Луч падает под прямым углом в среду, для которой
Пусть луч входящий — собственный вектор · Луч отраженный равен · Луч преломленный равен Таким образом, в данном случае оператором, действующим на собственные вектора является сама среда:
Пример 3. Если матрица
Таким образом, определение собственного вектора (1) (словесная формулировка): Если
|

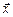 называется собственным вектором матрицы (оператора) А, если выполняется:
называется собственным вектором матрицы (оператора) А, если выполняется: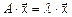 ,
, — собственные значения матрицы (оператора) А.
— собственные значения матрицы (оператора) А.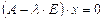 ,
,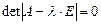 — характеристическое уравнение.
— характеристическое уравнение.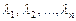 оператора А различны. Тогда соответствующие им собственные вектора
оператора А различны. Тогда соответствующие им собственные вектора 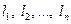 линейно независимы. (Собственные вектора, независимые между собой, образуют ортогональный базис).
линейно независимы. (Собственные вектора, независимые между собой, образуют ортогональный базис).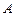 имеет n различных корней, то в некотором базисе матрица оператора А имеет диагональный вид. Если этот базис составлен из собственных векторов, а
имеет n различных корней, то в некотором базисе матрица оператора А имеет диагональный вид. Если этот базис составлен из собственных векторов, а  — матрица, состоящая из собственных векторов, то эта матрица
— матрица, состоящая из собственных векторов, то эта матрица 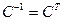 , матрица оператор А — симметричная, т.е.
, матрица оператор А — симметричная, т.е.  , тогда
, тогда 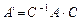 — диагональная, причем впоследствии покажем, что по ее диагонали будут расположены собственные значения
— диагональная, причем впоследствии покажем, что по ее диагонали будут расположены собственные значения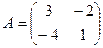 .
. - собственное число.
- собственное число.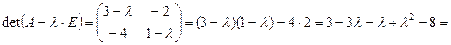
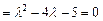 ,
,

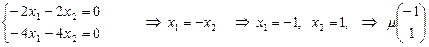 , где
, где 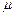 — произвольное число.
— произвольное число.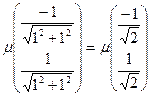 .
.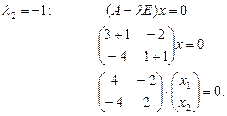
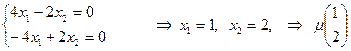
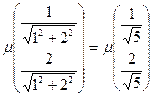 .
.
 и
и 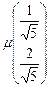 .
. .
.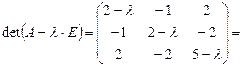
 .
.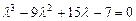 .
. . Поделим на него многочлен, впоследствии решим квадратное уравнение и получим три искомых корня:
. Поделим на него многочлен, впоследствии решим квадратное уравнение и получим три искомых корня: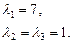
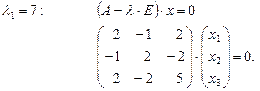
 ,
,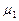 — произвольное число.
— произвольное число.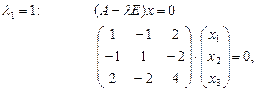
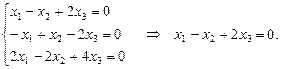
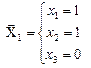 и
и 
 .
. .
. .
. .
.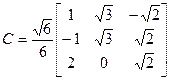

 имеем:
имеем: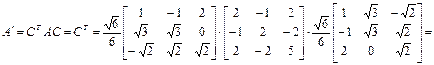

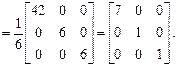
 имеет диагональный вид, по диагоналям расположены собственные значения:
имеет диагональный вид, по диагоналям расположены собственные значения: .
. .
.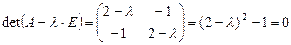 ,
,

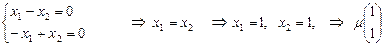 ,
, — произвольное число.
— произвольное число.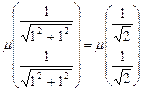 .
.

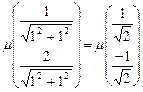 .
.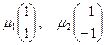 .
. .
.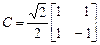 .
.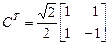

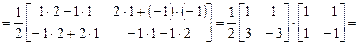

 .
. (Рис.1)
(Рис.1)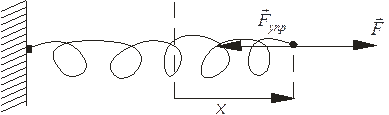 (Рис.2)
(Рис.2)
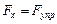
 ) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:
) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации: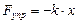

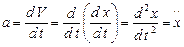
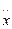 — есть принятое в физике обозначение второй производной по времени. Подставив в исходное уравнение, имеем;
— есть принятое в физике обозначение второй производной по времени. Подставив в исходное уравнение, имеем; ,
, .
.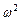 — Круговая частота свободных колебаний груза на пружине, собственная частота колебательной системы или угловая скорость для математического маятника, равная
— Круговая частота свободных колебаний груза на пружине, собственная частота колебательной системы или угловая скорость для математического маятника, равная .
. .
. , что он преобразуется в
, что он преобразуется в 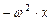 .
.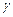 равен углу падения
равен углу падения 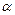 .
. есть величина, постоянная для двух данных сред:
есть величина, постоянная для двух данных сред:

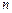 (относительный показатель преломления второй среды относительно первой) равен 1.
(относительный показатель преломления второй среды относительно первой) равен 1.

 ;
; .
.


