Семинар 3. Биномиальное распределениеЕсли случайное событие имеет только два исхода, причем вероятность реализации p одного из исходов в единичном испытании постоянна, то распределение вероятностей называется биномиальным. Условие нормировки в этом случае отражает альтернативный характер исхода: p + q = 1, где q – вероятность того, что событие не произошло. Биномиальное распределение отвечает на вопрос: какова вероятность реализации m определенных исходов в n независимых испытаниях при известном значении p? В статистике этот вопрос часто формулируется так: Какова вероятность обнаружить у m объектов (частиц) из n определенный признак? Биномиальное распределение справедливо для описания случайных событий, имеющих две возможности исхода, в различных областях повседневной жизни, медицине, науке: производстве и имеет следующее математическое выражение:
где Для расчета среднего значения m и дисперсии необходимо вычислить <mk>;, где k = 1, 2 согласно (2.3). В силу трудоемкости вычислений подобного рода, процедура суммирования заменяется эквивалентной по результату, но более простой по форме дифференциальной процедурой:
Существуют два важнейших предельных случая биномиального распределения. Распределение Гаусса (другое его название - нормальное распределение). При
В этом предельном случае m является непрерывно изменяющейся величиной (ámñ;>>1). Примерами нормального распределения являются: закон ошибок в метрологии, распределение попаданий в мишень (прицельная стрельба), распределение молекул по компонентам скорости в состоянии теплового равновесия. Распределение Пуассона (закон редких событий).
Распределение Пуассона описывает вероятности редких событий, когда
|

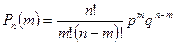 , (3.1)
, (3.1) – число способов, которыми можно выбрать m различных предметов из n различных предметов (число сочетаний).
– число способов, которыми можно выбрать m различных предметов из n различных предметов (число сочетаний). . (3.2)
. (3.2) и p = const, распределение плотности вероятности имеет вид
и p = const, распределение плотности вероятности имеет вид . (3.3)
. (3.3) При
При 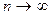 и np = const (p<<1)
и np = const (p<<1) (3.4)
(3.4)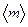 невелико по сравнению с 1. Такими событиями могут быть технические катастрофы, биологические мутации, молекулярное истечение - эффузия, вылет частиц при радиоактивном распаде ядра. Расчет флуктуаций в этом предельном случае упрощается:
невелико по сравнению с 1. Такими событиями могут быть технические катастрофы, биологические мутации, молекулярное истечение - эффузия, вылет частиц при радиоактивном распаде ядра. Расчет флуктуаций в этом предельном случае упрощается: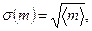
 . (3.5)
. (3.5)


