Проверка истинности тождеств при помощи диаграмм Эйлера-ВеннаВсе законы алгебры множеств можно наглядно представить и доказать, используя диаграммы Эйлера-Венна. Для этого необходимо: 1. Начертить соответствующую диаграмму и заштриховать все множества, стоящие в левой части равенства. 2. Начертить другую диаграмму и сделать то же для правой части равенства. 3. Данное тождество истинно тогда и только тогда, когда на обеих диаграммах заштрихована одна и та же область. Замечание 3.1. Два пересекающихся круга делят всё универсальное множество на четыре области (см. рис.3.1)
1. А Ç В; 2. А Ç 3. 4.
Рис.3.1 Замечание 3.2. Три пересекающихся круга делят всё универсальное множество на восемь областей (см. рис.3.2):
I. А Ç В Ç С; II. III. А Ç IV. А Ç V.
 Ç В Ç С; Ç В Ç С;
VI. VII. VIII. Замечание 3.2. При записи условий различных примеров часто используются обозначения: Þ - из … следует…; Û - тогда и только тогда, когда…. Задача 3.1. Упростить выражения алгебры множеств: 1) 2) 3) Решение. 1) 2) 3)
Задача 3.2. Доказать тождества: 1) (АÈВ)\В = А\В; 2) АÇ(ВÈС) = А\(А\В)Ç(А\С). Решение. 1) 2)
Задача 3.3. Доказать следующие соотношения двумя способами: с помощью диаграмм и с помощью определения равенства множеств. а) б) AÇ(BÈC) = (AÇB)È(AÇC); в) г) Решение. а) 1. Доказательство с помощью диаграммы:
2. Доказательство с помощью определения равенства множеств. По определению, множества Х и Y равны, если одновременно выполнены соотношения: XÍY и YÍX. Сначала покажем, что Теперь докажем обратное, то есть, что Значит, б) AÇ(BÈC) = (AÇB)È(AÇC); 1. Доказательство с помощью диаграммы:
2. Доказательство с помощью определения равенства множеств. Пусть х ÎАÇ(ВÈС). Тогда х ÎА и х ÎВÈС. Если х ÎВ, то х ÎАÇВ, что не противоречит сказанному, а значит, х Î(АÇВ)È(АÇС). Если же х ÎС, то х ÎАÇС. Следовательно, х Î(AÇB)È(AÇC). Итак, доказано, что AÇ(BÈC) Í (AÇB)È(AÇC. Пусть теперь х Î (AÇB)È(AÇC). Если х ÎАÇВ, то х ÎА и х ÎВ. Отсюда следует, что х ÎА и х ÎВÈС, то есть х ÎАÇ(ВÈС). Если же х ÎАÇС, то х ÎА и х ÎС. Отсюда вытекает, что х ÎА и х ÎВÈС, то есть х ÎАÇ(ВÈС). Таким образом, (AÇB)È(AÇC)Í AÇ(BÈC). Следовательно, AÇ(BÈC) = (AÇB)È(AÇC). Что и требовалось доказать. в)
При доказательстве достаточности мы получили, что АÇВ=Æ. Очевидно, что ÆÌС, поэтому соотношение доказано. При доказательстве был рассмотрен самый общий случай. Однако здесь возможны ещё некоторые варианты при построении диаграмм. Например, случай равенства АÇВ=С либо 2. Доказательство с помощью определения равенства множеств. Необходимость. Пусть АÇВÍС и элемент х ÎА. Покажем, что в этом случае элемент множества А будет являться также и элементом множества Рассмотрим два случая: х ÎВ или Если х ÎВ, то х ÎАÇВÍС, то есть х ÎС, и, как следствие этого, Если же Пусть теперь Если х ÎАÇВ, тогда х ÎА и х ÎВ. Поскольку г) 1. Доказательство с помощью диаграммы:
2. Доказательство с помощью определения равенства множеств. Пусть АÍВ. Рассмотрим элемент х ÏВ (или
Задача 3.4. Выразить символически указанные области и упростить полученные выражения.
Решение. 1. Искомая область состоит из двух изолированных частей. Условно назовём их верхней и нижней. Множество, которое они изображают, можно описать так: М = { xôx ÎA и х ÎВ и х ÏС или х ÎС и х ÏА и х ÏВ}. Из определения операций над множествами получим: М = ((АÇВ)\С)È(С\А\В). Запишем это выражение с помощью основных операций – дополнения, объединения и пересечения:
Упростить это выражения нельзя, поскольку имеем по одному вхождению каждого символа. Это и есть простейший вид данной формулы. 2. Данную область можно рассматривать как объединение множеств А\В\С и АÇВÇС. По определению M = { x ô x ÎA и x ÏВ и х ÏС или х ÎА и х ÎВ и х ÎС}. Упростим:
Задачи для самостоятельного решения. 1. Упростить: а) б) (А¸В)È(АÇВ); (ответ АÈВ); в) 2. Доказать с помощью диаграмм, законов алгебры множеств и определения равенства множеств: а) (АÈВ)\В = А\В; б) АÇ(ВÈС) = А\(А\В)Ç(А\С); в) АÈВ = АÇВ Þ А=В; г) А\В = Æ Û АÇВ = А. 3. Выяснить, существует ли множество Х, удовлетворяющее при любом А равенству: а) АÈХ = А; (ответ Æ); б) АÇХ = А; (ответ U).
|


 ;
;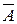 Ç В;
Ç В; А Ç В Ç
А Ç В Ç  ;
; Ç С;
Ç С;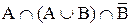 ;
;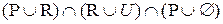 ;
; .
. ;
;





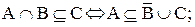


 . Пусть х – произвольный элемент множества
. Пусть х – произвольный элемент множества  , то есть х Î
, то есть х Î  . Отсюда вытекает, что х ÏА или х ÏВ. Если х ÏА, то тогда х ÎĀ, а значит,
. Отсюда вытекает, что х ÏА или х ÏВ. Если х ÏА, то тогда х ÎĀ, а значит, 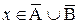 . Если же х ÏВ, то
. Если же х ÏВ, то  , а значит,
, а значит,  . есть также элементом множества
. есть также элементом множества 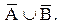 То есть
То есть 
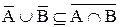 . Пусть
. Пусть  . Если же
. Если же  является также элементом множества
является также элементом множества 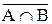 , то есть
, то есть 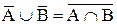 , что и требовалось доказать.
, что и требовалось доказать.

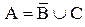 , случай пустых множества и так далее. Очевидно, что все возможные варианты учесть бывает затруднительно. Поэтому считается, что доказательство соотношений с помощью диаграмм не всегда является корректным.
, случай пустых множества и так далее. Очевидно, что все возможные варианты учесть бывает затруднительно. Поэтому считается, что доказательство соотношений с помощью диаграмм не всегда является корректным. .
. .
. и х ÎАÇВ. Покажем, что элемент х также будет элементом множества С.
и х ÎАÇВ. Покажем, что элемент х также будет элементом множества С. будет подмножеством множества Ā.
будет подмножеством множества Ā.
 . Что и требовалось доказать.
. Что и требовалось доказать.
 .
.

 (ответ V).
(ответ V).


