Динамическое программирование: 3 модели управления запасами1.Теория Задачи управления запасами возникают, когда необходимо сделать запас материальных ресурсов или предметов потребления с целью удовлетворения спроса на заданном интервале времени. Любая модель должна ответить на 2 вопроса: 1) какое количество продукции заказывать (ответ на? обычно получается из задачи минимизации суммарных затрат в выбранную ед.времени); 2) когда заказывать (ответ на? зависит от типа контроля над уровнем запаса). Контроль бывает периодическим: осущ-ние контроля в конце какого-то периода t(t запаса совпадает с одним из моментов контроля) и непрерывным( определяется точка заказа – объем товара на складе, при котором нужно сделать новый заказ). Модели делятся: 1) Детерминированные (все параметры – неслучайные величины): - статические: интенсивность потребления остается неизменной во времени - динамические: спрос известен достоверно, но изменяется в зависимости от времени 2) Вероятностные (часть параметров – случайные величины): - стационарные (функция плотности вероятности спроса неизменна во времени) - не стационарные (функция плотности вероятности спроса изменяется во времени) Затраты на приобретение(С) становятся важным фактором, когда цена единицы продукции зависит от размера заказа, что обычно выражается в виде оптовых скидок в тех случаях, когда цена единицы продукции убывает с возрастанием размера заказа. Затраты на оформление заказа(К) представляют собой постоянные расходы, связанные с его размещением. При удовлетворении спроса в течение заданного периода времени путем размещения более мелких заказов (более часто) затраты возрастают по сравнению со случаем, когда спрос удовлетворяется посредством размещения более крупных заказов (и, следовательно реже). Затраты на хранение запаса(Н), которые представляют собой расходы на содержание запаса на складе (затраты на переработку, амортизационные расходы, эксплуатационные расходы) обычно возрастают с увеличением уровня запаса. Потери от дефицита представляют собой расходы, обусловленные отсутствием запаса необходимой продукции. Оптимальный уровень запаса соответствует минимуму суммарных затрат.
y – объем заказа. Не допускается дефицит. К – стоимость оформления заказа h – стоимость хранения ед. товара в ед. времени
q – размер заказа, при превышении которого предоставляется скидка.
2.Однопродуктовая статическая модель без дефицита Эту модель можно интерпретировать как модель управления запасами в магазине. Руководство магазина закупает товар у оптовиков по цене c1 за единицу товара, если объем закупаемой партии y < q. Если у>= q, делается скидка и цена единицы товара становится равной c2 < c1. Затраты при закупке товара состоят из двух величин: условно постоянной величины:стоимостью оформления заказа(K). Переменной величины ¾ стоимости закупаемой партии равной c(y)y. Здесь c(y) равно c1,если y < q и равно c2, если y ³ q. В рассматриваемой модели предполагается, что в магазине спрос на товар в единицу времени является величиной постоянной и принимает значение равное b. Магазин также, несет расходы по хранению товара на собственном складе. В каждую единицу времени (час, день ит.д.) эти расходы составляют величину h за каждую единицу товара, находящуюся на складе в эту единицу времени. После оформления заказа товар поступает на склад магазина через интервал времени длиной t*. Руководству нужно определить, какое количество y товара заказывать, и точку заказа R с тем, чтобы суммарные затраты в единицу времени на закупку продаваемого товара и хранение товара на складе было минимальным. Затраты будут состоять из суммы трех величин: затрат на приобретение продаваемого товара, затрат на оформление заказа, затрат на хранение товара на собственном складе. ри минимальных затратах новая партия поступает на склад магазина в момент, когда весь товар израсходован. Следовательно, максимальное количество товара на складе равно y в момент поставки. График зависимости количества товара на складе от времени показан на рисунке 2. Ось x ¾ ось времени, а ось y ¾ значение величины запаса на складе. Вычислим средние затраты в единицу времени S(y). Отметим, что это можно сделать для одного периода [0; D1], так как на остальных периодах все вычисления будут полностью совпадать. В момент t=0 на складе имеется максимальное количество запаса равное y. В единицу времени расходуется b единиц запаса, следовательно, весь запас будет израсходован за время t = y/b
у
в c А F
0 E G D1 D2 D3 За рассматриваемое время заказ будет оформляться один раз, а расходы на оформление заказа в единицу времени составят K/ t = Kb/y. (2) Так как величина запаса будет различной в каждую единицу времени, то и расходы по хранению будут различны. Проведем в D0В D1 среднюю линию AC и опустим перпендикуляр CE.В силу равенства треугольников DABC и DECD1, величина запаса в любой точке левее точки E больше величины 0A= y/2 настолько, насколько меньше этой величины в точке, симметричной относительно E. Поэтому на всем отрезке [0; D1] можно считать, что в среднем хранится величина y/2. Таким образом, для величины средних затрат в единицу времени получаем следующее выражение S1(y)= c1β + Kb/y + hy/2, (3) если y<q и S2(y)= c2β + Kb/y + hy/2 (4) в противном случае. Здесь первое слагаемое выражает затраты на закупку товара продаваемого магазином в единицу времени. Второе ― затраты на оформление заказа отнесенные к единице времени. Третье ― средние затраты на хранение запаса в единицу времени. Так как первое слагаемое в зависимости от y меняется один раз на постоянную величину, то минимум у этих функций достигается в одной точке. Найдем минимум этого выражения по величине заказа y. Для этого вычислим производную и приравняем ее нулю. Из равенства (5) получаем формулу экономичного размера заказа Уилсона y*= Если бы цена на товар была постоянной (не зависела от объема закупаемой партии), то величина y* была бы оптимальной. Действительно, вторая производная функции Si(y) больше нуля в области y> 0. Следовательно, функция Si(y) выпуклая в этой области, а точка y* доставляет минимум этой функции. В случае разрыва цен величина оптимальной партии yopt зависит от величины q. S 1(q)
Если y* ³ q, тогда yopt = y*. Так как в этом случае при закупке партии в объеме y* будет получена скидка и суммарные затраты в единицу времени составят наименьшую из всех величину S2(y*). Пусть y* < q, тогда yopt = q, если q £ y1. Здесь y1 ¾ больший корень уравнения S1(y*) = S2(y). (7) Если же q > y1, то yopt = y*. Таким образом, если q £ y1, то выгодно воспользоваться скидкой, в противном случае ¾ нет (смотри рис. 2). Пусть оптимальный объем заказываемой партии определен и равен yopt. Точку заказа R определяется из соотношений R = b´t*, t* < t; R = b´(t*-m´t), где m ¾ целая часть от деления t* на t, а t = yopt /b. Так на рис 1 величина t* равна длине отрезка [ G; D 3]. При этом m =2, а величина R показана на оси y.
3.Однопродуктовая статическая модель с дефицитом В отличие от предыдущего пункта в данной модели предполагается, что цена на товар величина постоянная. Допускается дефицит. Как и ранее товар поставляется партиями через некоторые промежутки времени t. Интервал [0;C] длиной t делится на два (смотри рис.3). В течение первого интервала [0;A) длительностью t1 непрерывный спрос интенсивностью b удовлетворяется из запаса, имеющегося на складе. В течение второго интервала [A;C] длительностью t2 спрос не удовлетворяется. Накопленный неудовлетворенный спрос покрывается немедленно при поступлении следующей партии товара. За несвоевременную поставку товара взимается штраф. Штраф может толковаться и как штрафные санкции, и как упущенная прибыль. Будем предполагать, что взимается p денежных единиц за единицу недопоставленного товара в течение единицы времени.
y t*- время выполнения заказа; B h - стоимость хранения единицы товара в единицу времени; t - длина интервала [0, C] между поставками; H-суммарные затраты на периоде между поставками ([0;C]); А С t1 - длина интервала [0, A]; t2 - длина интервала [A, C].
D E
Обозначим: y - объем заказываемой партии (длина отрезка [D;B]); q - максимальное количество товара на складе (длина отрезка [0;B]). В рассматриваемой задаче нужно выбрать два параметра: y и q. Цель – минимизация суммарных затрат в единицу времени. Можно найти суммарные затраты на периоде от момента поставки товара до следующего момента поставки. Затем разделить их на длину периода и получить суммарные затраты в единицу времени. Выразим величины t1 и t2 через величину t. Из подобия треугольников DDBE, D0BC и DACE получаем: На рассматриваемом интервале [0, C] только в течение интервала [0, A] на складе имеется запас товара и, следовательно, затраты по хранению товара. Аналогично, только на интервале [A, C] имеется дефицит и затраты связанные с ним. Как и в предыдущей задаче, средний уровень запаса на складе на интервале [0, A] равен q/2. Средний уровень дефицита в течение интервала [A, C] равен (y-q)/2. Тогда затраты на хранение и потери от дефицита на отрезке [0, C] будут, соответственно, следующие:
Суммарные затраты на отрезке [0, C] будут состоять из этих затрат и затрат на оформление заказа. Заменяя t1 и t2 из соотношения (8), получим Найдем суммарные затраты в единицу времени, разделив величину H на длину рассматриваемого интервала t (как и в предыдущей задаче t = y/b).
Запишем необходимое условие минимума.
Разрешая данные уравнения относительно y и q, получаем:
При этом длина периода и минимальные суммарные затраты будут задаваться соотношениями
Отметим, что при этом т.е. отношение стоимостей хранения и стоимости дефицита единицы товара в единицу времени обратно пропорционально отношению максимального объема запаса и максимального объема дефицита. Найдем теперь точку заказа R. В отличие от предыдущей модели в момент заказа на складе может либо быть некоторое количество товара, либо накоплен некоторый объем дефицита. Поэтому под точкой заказа будем понимать объем либо товара, либо дефицита при котором нужно делать новый заказ. Так же как и в модели без дефицита, нужно для оптимального объема заказа y* определить величину t* (смотри (12)). Затем найти число m равное целой части от деления t* на t*и число t* = t* - m´ t*. Тогда точку заказа можно найти из соотношения
Первая строчка соответствует точке заказа равной объему товара, при котором нужно делать новый заказ, а вторая объему дефицита.
4.Многопродукт. статич. модель без дефицита (с ограничением на емкость складских помещений) Эта модель предназначена для систем управления запасами, включающие n(>1) видов продукции, которая хранится на одном складе ограниченной площади. Данное условие определяет взаимосвязь между различными видами продукции может быть включено в модель как ограничение. Пусть А – максимально допустимая площадь складского помещения для n видов продукции; предположим, что площадь, необходимая для хранения единицы продукции i -го вида, то ограничение на потребность в складском помещении принимают вид Допустим, что запас продукции каждого вида пополняется мгновенно и скидки цен отсутствуют. Предположим далее, что дефицит не допускается. Пусть bi, Ki и hi – интенсивность спроса, затраты на оформление заказа и затраты на хранение единицы продукции в единицу времени для i -го вида продукции соответственно. Общие затраты по продукции каждого вида, по существу, будут теми же, что и в случае эквивалентной однопродуктовой модели. Т.о., рассматриваемая задача имеет вид Общее решение этой задачи находится методом множителей Лагранжа. Однако, прежде чем применять этот метод, необходимо установить, действуют ли указанное ограничение, проверив выполнимость ограничений на площадь склада для решения Ограничение действует, если оно не выполняется для значений Оптимальные значения yi и l можно найти, приравняв нулю соответствующие частные производные, что дает
Заметим, что
|

 - количество ед. товаров в ед. времени
- количество ед. товаров в ед. времени - цена, если объем закупаемого товара меньше q
- цена, если объем закупаемого товара меньше q - цена, если объем закупаемого товара
- цена, если объем закупаемого товара  .
. 
 -время выполнения заказа
-время выполнения заказа (1)
(1) R
R - Kb/y2 + h/2 = 0. i=1,2 (5)
- Kb/y2 + h/2 = 0. i=1,2 (5) . (6)
. (6)
 K - стоимость оформления заказа;
K - стоимость оформления заказа;

 . Следовательно,
. Следовательно,  ;
;  (8)
(8) ,
,  .
. . (9)
. (9) . (10)
. (10) ;
;  .
. ;
;  . (11)
. (11) ;
;  . (12)
. (12) ,
, (13)
(13) .
. →MIN при
→MIN при 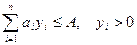
 для всех i.
для всех i. неограниченной задачи. Если ограничение выполняется, то оно избыточно, и им можно пренебречь.
неограниченной задачи. Если ограничение выполняется, то оно избыточно, и им можно пренебречь. . В таком случае нужно найти новое оптимальное значение yi, удовлетворяющее ограничению на площадь склада в виде равенства. Этот результат достигается построением функции Лагранжа вида
. В таком случае нужно найти новое оптимальное значение yi, удовлетворяющее ограничению на площадь склада в виде равенства. Этот результат достигается построением функции Лагранжа вида  , где l(<0) – множитель Лагранжа.
, где l(<0) – множитель Лагранжа. ,
, 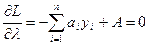 Из второго уравнения следует, что значение
Из второго уравнения следует, что значение  .
.


