Свойства равномерно сходящихся рядов
Свойство 1 (о непрерывности суммы ряда ) Если члены ряда в области Свойство 2 (о почленном интегрировании ряда) Если члены ряда на некоторой дуге то ряд можно почленно интегрировать вдоль этой дуги, т.е. Свойство 3 (о почленном дифференцировании ряда с вещественными членами) Пусть дан ряд с вещественными членами то функция и при этом
Степенные ряды Определение степенного ряда Функциональный ряд вида где
то степенной ряд имеет вид Теорема Абеля Если ряд то он сходится абсолютно при любом при этом он сходится равномерно на любом промежутке Если ряд в точке
|
непрерывны
, и ряд 
сходится равномерно в этой области, то его сумма 
непрерывна в 
.
непрерывны
, и ряд сходится равномерно на этой дуге к функции 
,
, члены которого на отрезке 
непрерывны вместе со своими производными. Если на 
данный ряд сходится к функции 
, а ряд из производных 
сходится равномерно на 
дифференцируема на 
.
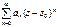называется степенным рядом,
– вещественные или комплексные числа, не зависящие от 
, называются коэффициентами степенного ряда;
– фиксированное число, называется центром сходимости степенного ряда. Если 
,
.
,
;
.
расходится, то он расходится во всех точках 
