Трехкратные повороты- Vocabulary game in net: https://www.youtube.com/watch?v=9D8oVMfBv54 – 2 hours - Reading the text “On the Move” – 4 hours
- Make a vocabulary with new definitions about the topic “Transport” – 2 hours, no less than 150 words – 2 hours
- Academic writing: Comparing data – 8 hours
Трехкратные повороты
Матрицу поворота, определяющую произвольную ориентацию одной системы координат относительно другой, можно представить в виде произведения трех матриц элементарных поворотов
где Матрицы элементарных поворотов имеют следующий вид
где введены сокращенные обозначения Для этих матриц можно записать следующее общее выражение
где В выражении (1) должны выполняться условия
Комбинация {1,2,3} соответствует углам Брайнта, их также называют углами Кардана. Комбинации {3,1,3}, {3,2,3}, {3,2,1} соответствуют 1, 2, 3 системам поворотов в углах Эйлера. Комбинация {2,1,3} соответствует корабельным углам Крылова. Комбинация {2,3,1} соответствует самолетным углам {угол рыскания, угол тангажа, угол крена}. На основании взаимной ортогональности единичных векторов
Обозначим индексом 1 исходную систему координат, а систему координат, полученную в результате трехкратного поворота от нее индексом 2. Используя (2),(3) можно получить выражения для элементов матрицы поворота
В случае
В случае
Предположим, что значения элементов матрицы поворота (4),(5) известны
Тогда можно получить решения для тригонометрических функций углов поворота. В случае
Для решения (6) имеем особый случай при
где В случае
Для решения (8) имеем особый случай при
Используя выражения для матриц поворота (4), (5) можно получить выражения для матриц
где Продифференцировав (10) можно получить выражение для векторов
Отметим, что
где в качестве В случае
В случае
Рассмотрим условия вырожденности матрицы В случае
В случае
Если матрица
В случае
В случае
|





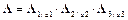 , (1)
, (1)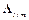 - матрица
- матрица  -го элементарного поворота вокруг оси
-го элементарного поворота вокруг оси  на угол
на угол  . Значение
. Значение 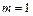 соответствует повороту вокруг оси
соответствует повороту вокруг оси 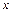 ,
,  – вокруг оси
– вокруг оси  и
и  – вокруг оси
– вокруг оси  .
. ,
,  ,
,  ,
, ,
,  для тригонометрических функций углов поворота
для тригонометрических функций углов поворота  , (2)
, (2)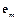 - единичный вектор оси с номером
- единичный вектор оси с номером  .
. и
и  , поскольку соседние повороты не должны производиться вокруг одной и той же оси. Поэтому возможны только следующие 12 комбинаций поворотов
, поскольку соседние повороты не должны производиться вокруг одной и той же оси. Поэтому возможны только следующие 12 комбинаций поворотов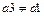 :
:  ;
;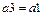 :
:  .
. можно получить следующие выражения
можно получить следующие выражения ,
, 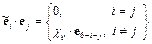 ,
,  ,
, , (3)
, (3) ,
,  -
- 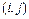 -й элемент матрицы
-й элемент матрицы  ,
, ,
,  ,
, 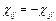 .
. в выражении (1). В полученных выражениях и далее будут использоваться следующие обозначения
в выражении (1). В полученных выражениях и далее будут использоваться следующие обозначения ,
, ,
, .
. . (4)
. (4) . (5)
. (5) .
. ,
,  ,
,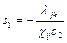 ,
,  , (6)
, (6) ,
,  .
. . При этом оси 1-го и 3-го поворотов совпадают. Из (6) получаем следующее решение для углов поворота для случая
. При этом оси 1-го и 3-го поворотов совпадают. Из (6) получаем следующее решение для углов поворота для случая  ,
, , (7)
, (7) ,
, .
. ,
, 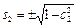 ,
, ,
,  , (8)
, (8) ,
,  ,
, . При этом оси 1-го и 3-го поворотов совпадают. Из (8) получаем следующее решение для углов поворота для случая
. При этом оси 1-го и 3-го поворотов совпадают. Из (8) получаем следующее решение для углов поворота для случая 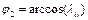 ,
, , (9)
, (9) .
. , с использованием которых угловые скорости систем координат определяются выражением
, с использованием которых угловые скорости систем координат определяются выражением , (10)
, (10) .
. в выражении для угловых ускорений систем координат
в выражении для угловых ускорений систем координат
 ;
;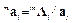 ,
, выступают
выступают  .
. и вектор
и вектор 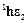 имеют следующие значения
имеют следующие значения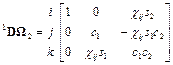 , (11)
, (11)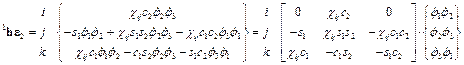 . (12)
. (12) , (13)
, (13) . (14)
. (14) , и получаем следующие условия вырождения матрицы
, и получаем следующие условия вырождения матрицы .
. , и получаем следующие условия вырождения матрицы
, и получаем следующие условия вырождения матрицы .
. . Используя обратную матрицу можно определить скорости и ускорения элементарных поворотов
. Используя обратную матрицу можно определить скорости и ускорения элементарных поворотов ,
, .
. определяется следующим выражением
определяется следующим выражением .
. .
.


