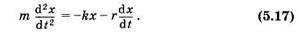Вестибулярный аппарат как инерциальная система ориентацииВ обычных условиях положение свободно подвешенного маятника указывает направление силы тяжести (рис. 4.8, а). Если маятник покоится относительно ускоренно движущейся системы отсчета (неинерциальная система отсчета), то его положение зависит от ускорения системы а (рис. 4.8, б). Как следует из рисунка, по второму закону Ньютона,
где результирующая сила равна по величине откуда
Следовательно, даже простой математический маятник в принципе может быть использован для определения модуля и направления ускорения системы. Более удобным индикатором ускорения системы является устройство, изображенное на рис. 4.9, — тело известной массы укреплено на шести пружинках. По деформации пружин
можно определить значение и направление силы, действующей на тело, а отсюда и ускорение системы, если учесть ускорение свободного падения. Такого рода индикаторы используются в инерциальной навигации, получившей развитие в связи с решением космических задач. В самом деле, если известно ускорение системы, например ракеты, в каждый момент времени, то можно найти зависимость скорости от времени: Определив v = f(t), можно найти положение системы в любой момент Наш организм приспособился к действию силы тяжести; соответствующую привычную информацию клетки вестибулярного аппарата сообщают в мозг, поэтому состояния невесомости и перегрузок воспринимаются нами посредством вестибулярного аппарата (и других органов) как необычные состояния, к которым необходимо приспособиться. Если оказывается периодическое воздействие на вестибулярный аппарат человека, например, при качке корабля, то это может привести организм в особое состояние, называемое морской болезнью.
Таким образом, можно без помощи средств, находящихся вне ракеты, автономно установить ее местоположение, скорость и ускорение в любой момент времени. Соответствующие устройства называются инерциальными системами ориентации. В человеческом организме имеется орган, который тоже, по существу, является инерциальной системой ориентации, — это вестибулярный аппарат. Он расположен во внутреннем ухе и состоит из трех взаимно перпендикулярных полукружных каналов К и полости — преддверия В (рис. 4.10). На внутренней поверхности стенок преддверия и в части полукружных каналов находятся группы чувствительных нервных клеток, имеющих свободные окончания в форме волосков. Внутри преддверия и полукружных каналов есть студенистая масса (эндолимфа), содержащая мелкие кислого кальция (отолиты). Ускоренное перемещение головы вызывает перемещение эндолимфы и отолитов, что воспринимается нервными клетками (через волоски). Вестибулярный аппарат, как и любая другая физическая система, не отличает гравитационное воздействие от воздействий, возникающих при ускоренном движении системы. Г Л А В А 5 Механические колебания и волны Повторяющиеся движения или изменения состояния называют колебаниями (переменный электрический ток, движение маятника, работа сердца и т. п.). Всем колебаниям, независимо от их природы, присущи некоторые общие закономерности. В зависимости от характера взаимодействия колеблющейся системы с окружающими телами различают колебания свободные, вынужденные и автоколебания. Колебания распространяются в среде в виде волн. В данной главе рассматриваются механические колебания и волны. § 5.1. § 5.1. Свободные механические колебания (незатухающие и затухающие) Свободными (собственными) колебаниями называют такие, которые совершаются без внешних воздействий за счет первоначально полученной телом энергии. Характерными моделями таких механических колебаний являются материальная точка на пружине (пружинный маятник) и материальная точка на нерастяжимой нити (математический маятник). В этих примерах колебания возникают либо за счет первоначальной потенциальной энергии (отклонение материальной точки 6т положения равновесия и движение без начальной скорости), либо за счет кинетической (телу сообщается скорость в начальном положении равновесия), либо за счет и той и другой энергии (сообщение скорости телу, отклоненному от положения равновесия). Рассмотрим пружинный маятник. В положении равновесия (рис. 5.1, а) упругая сила уравновешивает силу тяжести mg. Если оттянуть пружину на расстояние х (рис. 5.1, б), то на материальную точку будет действовать большая упругая сила. Изменение значения упругой силы (F), согласно закону Гука, пропорционально изменению длины пружины или смещению х точки:
где k — коэффициент пропорциональности между силой и смещением, который в данном случае является жесткостью пружины; знак минус показывает, что сила всегда направлена в сторону положения равновесия: F < 0 при х > О, F > О при х < 0. Другой пример. Математический маятник (рис. 5.2) отклонен от положения равновесия на такой небольшой угол α, чтобы можно было считать траекторию движения материальной точки прямой линией, совпадающей с осью ОХ. При этом выполняется приближенное равенство:
где х — смещение материальной точки относительно положения равновесия, I — длина нити маятника.
где k — коэффициент пропорциональности между силой и смещением, который в данном случае равен
На материальную точку (рис. 5.2) действуют сила натяжения нити F и сила тяжести mg, модуль их равнодействующей равен. Сравнивая (5.3) и (5.1), видим, что в этом примере равнодействующая сила подобна упругой, так как пропорциональна смещению материальной точки и направлена к положению равновесия. Такие силы, неупругие по природе, но аналогичные по свойствам силам, возникающим при малых деформациях упругих тел, называют квазиупругими. На материальные точки, рассмотренные в этих примерах, кроме упругой и квазиупругой силы действует и сила сопротивления |трения), модуль которой обозначим Fc (на рисунках не показана). Дифференциальное уравнение, описывающее движение материальной точки, получаем на основании второго закона Ньютона (произведение массы тела на его ускорение равно сумме всех действующих сил):
Выражение для смещения материальной точки, которое получается из решения этого уравнения, рассмотрим для некоторых частных случаев. Незатухающие колебания. Рассмотрим модель, в которой пренебрегают силой сопротивления (F с = 0). Из (5.5) имеем:
и преобразуя, получаем следующее дифференциальное уравнение второго порядка:
Его решение, в чем можно убедиться подстановкой, приводит к гармоническому колебанию:
где (ω0t + φ„ = φ — фаза колебаний, φ0 — начальная фаза (при t = 0), ω0 — круговая частота колебаний, А — их амплитуда. Амплитуда и начальная фаза колебаний определяются начальными условиями движения, т. е. положением и скоростью материальной точки в момент t = 0. Среди различных видов колебаний гармоническое колебание является наиболее простой формой.
Таким образом, материальная точка, подвешенная на пружине (пружинный маятник) или нити (математический маятник), совершает гармонические колебания, если не учитывать силы сопротивления. При преобразовании дифференциального уравнения гармонического колебания величина ю0 была введена формально [см. (5.6)], однако она имеет важный физический смысл, так как определяет частоту колебаний системы и показывает, от каких факторов (параметров) эта частота зависит: от жесткости пружины и массы в одном примере, длины нити и ускорения свободного падения в другом. Период колебаний может быть найден из формулы
На основании тригонометрических формул преобразуем (5.12):
Используя (5.6), получаем период колебаний пружинного маятника подставляя вместо k выражение (5.4), находим период колебаний математического маятника Очень удобно изображать гармонические колебания с помощью векторных диаграмм. Этот метод состоит в следующем. Из начала оси абсцисс проведем вектор А(рис.5.3), проекция которого на ось ОХ равна Acos φ. Если вектор А будет равномерно вращаться с угловой скоростью ю0 против часовой стрелки, то φ = ωоf+ φ0, где φ0 — начальное значение, и проекция вектора А на ось ОХ будет изменяться со временем по закону (5.8). В таком представлении амплитуда колебаний есть модуль равномерно вращающегося вектора А, фаза колебаний — угол между вектором А и осью ОХ, начальная фаза — начальное значение этого угла, круговая частота колебаний — угловая скорость вращения вектора А, смещение х колеблющейся точки — проекция вектора А на ось ОХ. где vm = Аω0 — максимальная скорость (амплитуда скорости).
Чтобы найти скорость материальной точки при гармоническом колебании, нужно взять производную от выражения (5.8) по времени:
Сравнивая (5.13) и (5.8), замечаем, что фаза скорости на π/2 больше фазы смещения, т. е. скорость опережает по фазе смещение на π/2. Продифференцировав (5.12), найдем ускорение:
где ат = Аω0 — максимальное ускорение (амплитуда ускорения). Вместо (5.14) запишем
Из сравнения (5.15) и (5.8) следует, что фазы ускорения и смещения различаются на п, т. е. эти величины изменяются в противофазе. Графики зависимости смещения, скорости и ускорения от времени показаны на рис. 5.4, а их векторные диаграммы — на рис. 5.5.
Допустим, что частоты складываемых колебаний одинаковы (ω1 = <ω2 = ω0), тогда результирующее смещение точки Выполним такое сложение с помощью векторной диаграммы. Изобразим положение векторов Аг и А„ в начальный момент времени (рис. 5.9), углы между этими век- торами и осью ОХ равны начальным фазам слагаемых колебаний ω1 и ω2. Вектор А — амплитуда результирующего колебания. Так как А1 и А2 вращаются с одинаковой угловой скоростью, то и сумма их — вектор А — будет вращаться с той же угловой скоростью, т. е. результирующее движение является гармоническим с круговой частотой ωо:
Выразим амплитуду А этого колебания и начальную фазу φ0 через заданные значения A1 А2, φ01 и φ02. Применяя теорему косинусов к треугольнику, заштрихованному на рис. 5.9, получаем
Как видно из рис. 5.9, tg φ равен отношению проекции А на ось OY к проекции А на ось ОХ, т. е. Ау/Ах. Учитывая, что проекция суммы равна сумме проекций, имеем:
Применительно к одномерному движению последней формуле
Подставим выражение (5.16) в уравнение (5.5) и получим:
Разделив обе части уравнения на т, запишем его в стандартной форме:
После замены получаем окончательную запись дифференциального уравнения свободных колебаний с учетом сил сопротивления:
где р — коэффициент затухания; ωо — круговая частота собственных колебаний системы (без затухания). График этой функции показан на рис. 5.6 сплошной кривой 1; штриховой линией 2 изображено изменение амплитуды:
Решение (5.19) существенно зависит от знака разности ω2 = ω— Р2, где ω — круговая частота затухающих колебаний. При ω2 - Р2 > 0 круговая частота ω является действительной величиной и решение уравнения (5.19) будет следующим: где значение Ао приведено на рисунке. Период затухающих колебаний зависит от коэффициента трения и определяется формулой:
При очень малом трении период затухающего колебания близок к периоду незатухающего свободного колебания:
Быстрота убывания амплитуды колебаний определяется коэффициентом затухания: чем сильнее тормозящее действие среды, тем больше р и тем быстрее уменьшается амплитуда. На практике, однако, степень затухания часто характеризуют логарифмическим декрементом затухания, понимая под этим величину, равную натуральному логарифму отношения двух последовательно.
Следовательно, коэффициент затухания и логарифмический документ затухания связаны достаточно простой зависимостью:
При сильном затухании φ2 > ω2 из формулы (5.22) видно, что период колебания является мнимой величиной. Движение в этом случае уже не будет периодическим и называется апериодическим.. Возможные апериодические движения представлены в виде графиков на рис. 5.7. Этот случай применительно к электрическим явлениям рассматривается в гл. 14.
|

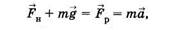






















 Затухающие колебания. В реальном случае на колеблющееся тело действуют силы сопротивления (трения), характер движения изменяется, и колебание становится затухающим. Для того чтобы из уравнения (5.5) найти временную зависимость затухающего колебания, необходимо знать, от каких параметров и как зависит сила сопротивления. Обычно предполагают, что при не очень больших амплитудах и частотах эта сила пропорциональна скорости движения и, естественно, направлена противоположно Скорости: Fc = -rv, где r — коэффициент трения (сопротивления), характеризующий свойства среды оказывать сопротивление.
Затухающие колебания. В реальном случае на колеблющееся тело действуют силы сопротивления (трения), характер движения изменяется, и колебание становится затухающим. Для того чтобы из уравнения (5.5) найти временную зависимость затухающего колебания, необходимо знать, от каких параметров и как зависит сила сопротивления. Обычно предполагают, что при не очень больших амплитудах и частотах эта сила пропорциональна скорости движения и, естественно, направлена противоположно Скорости: Fc = -rv, где r — коэффициент трения (сопротивления), характеризующий свойства среды оказывать сопротивление.