Функция от случайной величиныПусть на вероятностном пространстве (Ω, B, Р) задана случайная величина X = Х (ω). Рассмотрим действительную функцию у = Y (х) действительного аргумента х (область определения которой включает в себя множество возможных значений случайной величины X). Определение. Случайную величину Y,которая каждому элементарному исходу ωставит в соответствие число Y (ω) = Y (X (ω)) называют функцией Y (X)(скалярной)отскалярной случайной величины X. Функция Y = Y (X)от дискретной случайной величины также является дискретной случайной величиной, поскольку она не может принимать больше значений, чем случайная величина X. Функция Y = Y(X) от непрерывной случайной величины X может быть как непрерывной, так и дискретной (если, например, множество значений функции Y(X) конечное или счетное). В силу определения FY (y)представляет собой вероятность события { Y < у }, состоящего из тех элементарных исходов ω, для которых Y (Х (ω)) < у. Для этих же элементарных исходов ωслучайная величина Х (ω)будет принимать свои возможные значения на некоторой совокупности {Δ k }, k = 1,2,..., непересекающихся промежутков числовой прямой R. Иными словами, событие { Y (Х (ω)) < у }эквивалентно событию
Зная плотность распределения рX (х)случайной величины X, имеем
а следовательно, учитывая свойство аддитивности определенного интеграла, получаем
где сумма может быть и бесконечной. Поскольку совокупность промежутков {Δ k } определена как множество тех значений случайной величины Х (ω),для которых Y (Х (ω)) < у, то для множества
Последняя запись означает, что интегрирование проводится по всем тем значениям х, для которых Y (x)< у. Множество таких значений может представлять собой совокупность промежутков, и тогда нужно использовать свойство аддитивности интеграла, а пределы интегрирования по отдельным промежуткам определяются их границами. Найдем математическое ожидание функции от случайной величины. Рассмотрим сначала дискретную случайную величину Х принимающую значения x 1, ..., xn. Тогда случайная величина Y = Y (X) принимает значения Y (x 1),..., Y (xn)с вероятностями pi = P { X = xi } и ее математическое ожидание определяется формулой
Если же величина X принимает счетное число значений, то математическое ожидание Y определяется формулой
но при этом для существования математического ожидания требуется абсолютная сходимость соответствующего ряда
Для непрерывкой случайное величины X, имеющей плотность распределения р (х), математическое ожидание случайной величины Y = Y (X)можно найти, используя формулу
причем и здесь требуется выполнение условия
Теорема. Математическое ожидание удовлетворяет следующим свойствам. 1. Если случайная величина X принимает всего одно значение С с вероятностью единица (т.е., по сути дела, не является случайной величиной), то МС = С. 2. М (аХ + b) = aMХ + b, где а, b − постоянные. 3. М (Х 1 + Х 2) = МХ 1 + МХ 2. 4.
Теорема. Дисперсия удовлетворяет следующим свойствам. 1. Если случайная величина X принимает всего одно значение С с вероятностью единица, то DC = 0. 2. D (aX + b) = a 2 DX. 3. DX = MX 2 − (MX)2. 4. D (X + Y) = DX + Dy для независимых случайных величин X и Y.
|

 , и, следовательно, по расширенной аксиоме сложения вероятностей
, и, следовательно, по расширенной аксиоме сложения вероятностей


 , по которому ведется интегрирование, принято обозначение: Y (x) < y. Окончательно получаем
, по которому ведется интегрирование, принято обозначение: Y (x) < y. Окончательно получаем
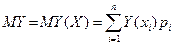
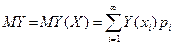

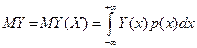

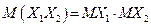 для независимых случайных величин Х 1 и Х 2.
для независимых случайных величин Х 1 и Х 2.
 3) и 4) утверждения можно доказать с использованием многомерной случайной величины и ее свойств.
3) и 4) утверждения можно доказать с использованием многомерной случайной величины и ее свойств.
 3) Далее, согласно свойствам 2 и 3 математического ожидания, получаем
3) Далее, согласно свойствам 2 и 3 математического ожидания, получаем
 4) Пусть X и Y − независимые случайные величины. Тогда, используя независимость случайных величин
4) Пусть X и Y − независимые случайные величины. Тогда, используя независимость случайных величин  и
и  , а также свойства 2-4 математического ожидания, получаем
, а также свойства 2-4 математического ожидания, получаем




