Поле бесконечно заряженной нитиРассмотрим бесконечную нить, несущую заряд, равномерно распределённый по её длине. Заряд, сосредоточенный на бесконечно нити, конечно, тоже бесконечен, и поэтому он не может служить количественной характеристикой степени заряженности нити. В качестве такой характеристики принимается «линейная плотность заряда». Эта величина равна заряду, распределённому на отрезке нити единичной длины:
Выясним, какова напряженность поля, создаваемого заряженной нитью на расстоянии а от неё (рис. 1.12).
Рис. 1.12. Для вычисления напряжённости вновь воспользуемся принципом суперпозиции электрических полей и законом Кулона. Выберем на нити элементарный участок dl. На этом участке сосредоточен заряд dq = t dl, который можно считать точечным. В точке А такой заряд создаёт поле (см. 1.3)
Исходя из симметрии задачи, можно заключить, что искомый вектор напряжённости поля
Рис. (1.12 b) позволяет сделать следующие заключения:
Таким образом
Используя (1.8) и (1.9) в уравнении (1.7), получим
Теперь для решения задачи осталось проинтегрировать (1.10) по всей длине нити. Это означает, что угол a будет меняться от
В этой задаче поле обладает цилиндрической симметрией. Напряжённость поля прямо пропорциональна линейной плотности заряда на нити t и обратно пропорциональна расстоянию а от нити до той точки, где измеряется напряжённость. Лекция 2 «Теорема Гаусса для электрического поля» План лекции 1.Поток вектора напряженности электрического поля. 2.Теорема Гаусса для электрического поля. 3.Применение теоремы Гаусса для расчёта электрических полей. 3.1. Поле бесконечной заряженной нити. 3.2. Поле бесконечной заряженной плоскости. Поле плоского конденсатора. 3.3. Поле сферического конденсатора.
Первую лекцию мы закончили расчётом напряжённости полей электрического диполя и бесконечно заряженной нити. В обоих случаях использовался принцип суперпозиции электрических полей. Теперь обратимся ещё к одному методу вычисления напряжённости, основанному на теореме Гаусса для электрического поля. В этой теореме речь идёт о потоке вектора напряжённости через произвольную замкнутую поверхность. Поэтому прежде чем преступить к формулировке и доказательству теоремы, обсудим понятие «поток вектора». 1. Поток вектора напряжённости электрического поля Выделим в однородном электрическом поле плоскую поверхность
Рис. 2.1. Но единичный нормальный вектор
Рис. 2.2. Если поле в общем случае неоднородно, а поверхность S, через которую следует вычислить поток, не плоская, то эту поверхность делят на элементарные участки
Здесь En = E ∙ cosa — проекция вектора напряжённости на направление нормали
Рис. 2.3. Теперь представим себе замкнутую поверхность в электрическом поле. Для отыскания потока вектора напряжённости через подобную поверхность проделаем следующие операции (рис. 2.4.): 1. Разделим поверхность на участки 2. Вычислим поток на каждом элементарном участке
Обратите внимание на то, что вектор 3. Для вычисления полного потока вектора напряжённости через всю замкнутую поверхность, все эти потоки нужно алгебраически сложить, то есть уравнение (2.3) проинтегрировать по замкнутой поверхности S
Кружок на знаке интеграл
Рис. 2.4. Напомним, что при графическом изображении полей, густота силовых линий в произвольной точке поля числено равна значению напряжённости поля в этой точке. Это означает, что
Тогда число силовых линий, пронизывающих поверхность dS, можно записать так dN = En ∙ dS = E ∙ dS ∙ cosa Но ведь это определение потока вектора напряжённости через поверхность dS. Таким образом, поток вектора напряжённости через поверхность dS численно равен числу силовых линий, пронизывающих эту поверхность (!). Этот вывод справедлив и для потока электрического поля через замкнутую поверхность: этот поток будет равен алгебраической сумме силовых линий втекающих (–) и вытекающих (+) из замкнутой поверхности. Теперь обратимся к теореме Гаусса.
|

 .
.

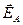 будет направлен по линии, перпендикулярной нити, то есть вдоль оси х. Поэтому сложение векторов напряжённости, можно заменить сложением их проекцией на это направление.
будет направлен по линии, перпендикулярной нити, то есть вдоль оси х. Поэтому сложение векторов напряжённости, можно заменить сложением их проекцией на это направление. (1.7)
(1.7) (1.8)
(1.8) . (1.9)
. (1.9) (1.10)
(1.10) до
до 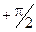 .
. (1.11)
(1.11)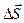 (рис. 2.1.). Эта поверхность — вектор, численно равный площади поверхности D S и направленный перпендикулярно поверхности
(рис. 2.1.). Эта поверхность — вектор, численно равный площади поверхности D S и направленный перпендикулярно поверхности (2.1)
(2.1)
 может быть направлен как в одну, так и в другую сторону от поверхности (рис. 2.2.). Произвольно выберем положительное направление нормали так, как это показано на рис. 2.1. По определению потоком вектора напряжённости электрического поля
может быть направлен как в одну, так и в другую сторону от поверхности (рис. 2.2.). Произвольно выберем положительное направление нормали так, как это показано на рис. 2.1. По определению потоком вектора напряжённости электрического поля  через выделенную поверхность
через выделенную поверхность  (2.2)
(2.2)
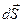 , в пределах которых напряжённость можно считать неизменённой, а сами участки — плоскими (рис. 2.3.) Поток вектора напряжённости через такой элементарный участок
, в пределах которых напряжённость можно считать неизменённой, а сами участки — плоскими (рис. 2.3.) Поток вектора напряжённости через такой элементарный участок  (2.3)
(2.3) . Полный поток через всю поверхность S найдём, проинтегрировав (2.3) по всей поверхности
. Полный поток через всю поверхность S найдём, проинтегрировав (2.3) по всей поверхности (2.4)
(2.4)
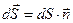 . Важно отметить при этом, что в случае замкнутой поверхности положительной считается только «внешняя» нормаль
. Важно отметить при этом, что в случае замкнутой поверхности положительной считается только «внешняя» нормаль  .
. :
:
 (2.5)
(2.5) означает, что интегрирование производится по замкнутой поверхности.
означает, что интегрирование производится по замкнутой поверхности.
 .
.


