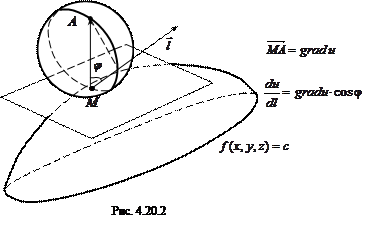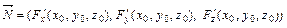Производная скалярного поля по направлению. Градиент
Как уже отмечалось, числовые функции нескольких переменных при анализе физических проблем часто называют скалярными полями (поле температур, давлений, электростатического потенциала и т.д.)
Будем считать, что точка x + D x, y + D y, z + D z, тогда
Запишем полное приращение функции: D u = f (x +D x, y +D y, z +D z)– – f (x, y, z). Если рассматриваемая функция является дифференцируемой, то согласно формуле Тейлора
Величина
называется производной скалярного поля по направлению вектора Для вычисления предела (4.20.2) разделим (4.20.1) на D l и учтем, что в силу условия D
Поэтому при D l
Вектор
называется градиентом11 скалярного поля в рассматриваемой точке М (x, y, z). Если ввести вектор
Таким образом, производная скалярного поля по направлению
Выясним теперь, как направлен градиент. Для этого введем так называемые поверхности уровня, т.е. поверхности, на которых значение рассматриваемой функции постоянно: f (x, y, z) = C (4.20.6) (вспомните знакомые из физики изотермы, изобары, эквипотенциальные поверхности и т.д.). Ранее отмечалось, что уравнение касательной плоскости к поверхности z = f (x, y) в точке
Если уравнение поверхности задано в неявном виде
Тогда
или окончательно
Уравнение касательной плоскости к поверхности (4.20.6), очевидно, должно совпадать с (4.20.7), так как наличие константы в правой части (4.20.6) не изменит рассматриваемых частных производных. Поэтому вектор grad u направлен по нормали к поверхности уровня (4.20.6) (нормальный вектор к плоскости (4.20.7) имеет вид
и совпадает с grad u (4.20.4)). Таким образом, градиент обладает следующими свойствами (рис. 4.20.2): 1) направлен по нормали к поверхности уровня; 2) производная по любому направлению равна проекции градиента на это направление. 10 Точка перегиба считается расположенной на самой кривой в отличие от точки экстремума, расположенной на оси абсцисс. Сама кривая считается гладкой, т.е. направление касательной на ней изменяется непрерывно (проанализировать понятие гладкости кривой самостоятельно). 11 [1] gradiens (лат.) – шагающий, идущий
|

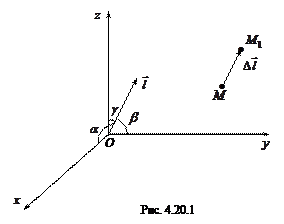 Рассмотрим скалярное поле
Рассмотрим скалярное поле 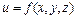 и проследим за тем, как оно изменяется в окрестности произвольной точки
и проследим за тем, как оно изменяется в окрестности произвольной точки 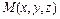 по выбранному направлению
по выбранному направлению 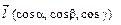 (рис.4.20.1). Для этого введем вектор
(рис.4.20.1). Для этого введем вектор 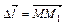 , сонаправленный с
, сонаправленный с  .
. имеет координаты:
имеет координаты:
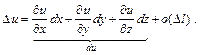 (4.20.1)
(4.20.1)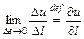 (4.20.2)
(4.20.2)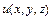 по рассматриваемому направлению.
по рассматриваемому направлению.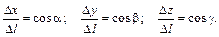
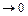 получим формулу для вычисления производной
получим формулу для вычисления производной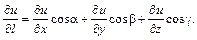 (4.20.3)
(4.20.3)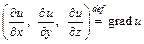 (4.20.4)
(4.20.4)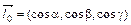 , то из (4.20.3) следует, что
, то из (4.20.3) следует, что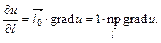
 (4.20.5)
(4.20.5)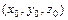 имеет вид
имеет вид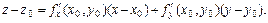
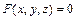 и оно определяет функцию
и оно определяет функцию 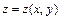 , то вместо
, то вместо 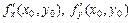 нужно подставить
нужно подставить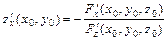 ;
;
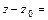
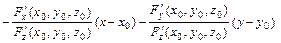
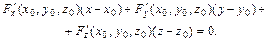 (4.20.7)
(4.20.7)