Температурная зависимость прыжковой проводимостиТемпературная зависимость особенно существенно для аморфных полупроводников, где уровни созданы не примесью, а искажениями самой структуры. Температура такая низкая, что 1. Таким образом можно отбросить вопрос разности уровней и построить скелет по принципу выделенных соседей
2. Пусть скелет бесконечного кластера будет как в 8.2.
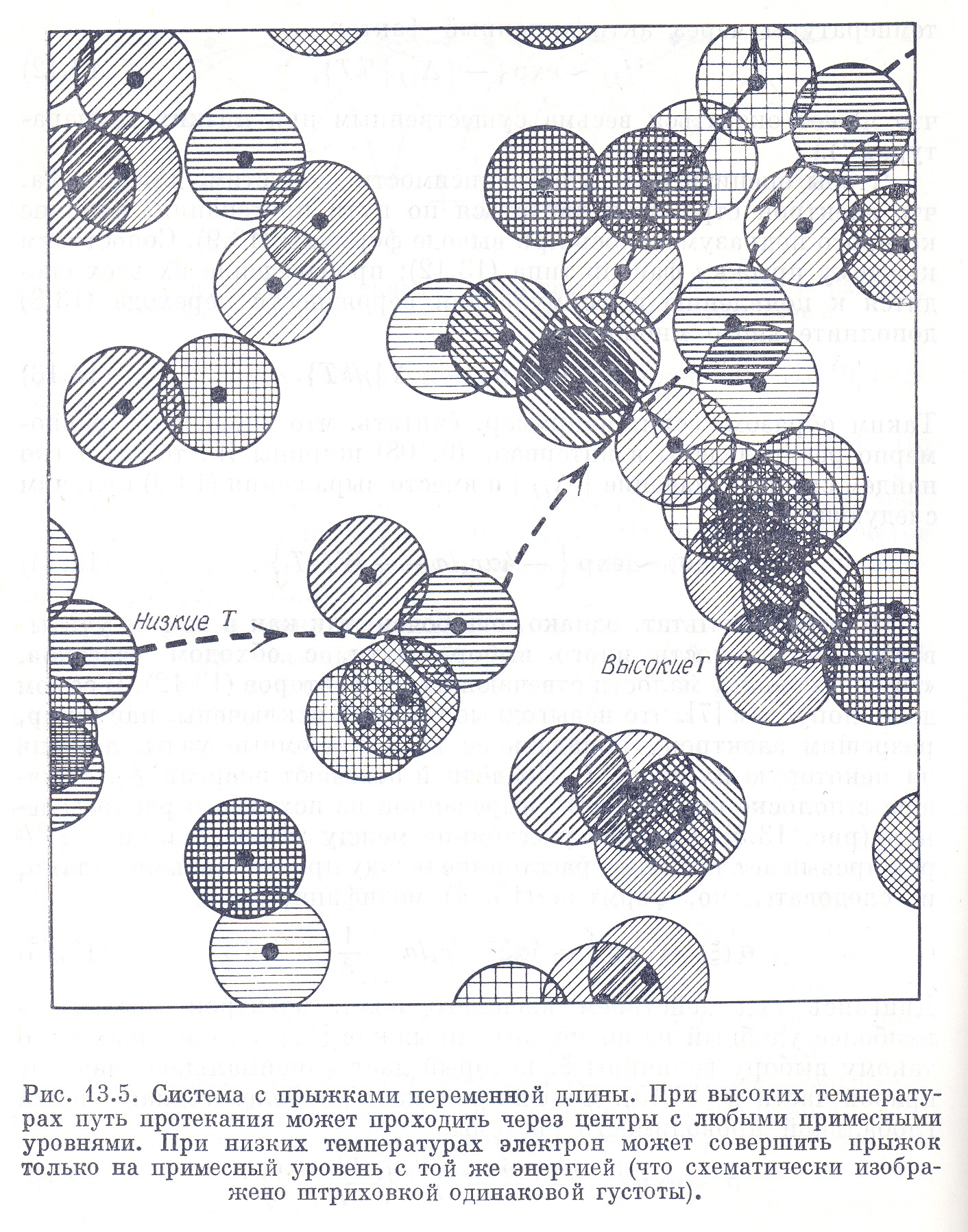
Рис. 8.8. Система с прыжками переменной длины.
При высоких температурах (рис. 8.8) путь протекания может проходить через центры с любыми примесными уровнями. При низких температурах электрон может совершить прыжок только на примесный уровень с той же энергией. На рис. 8.8 это показано кружками, одинаково густо заштрихованными.
Рис. 8.9. Уровни энергий примесей создают зону
Это соответствует зависимости
но при более низких температурах это не так. Величина W определяется количеством примесей, т.к. именно они определяют разброс энергетических уровней в энергетическом пространстве.
В бесконечном кластере, сформированном как показано в п.8.2, задействованы не все примесные центры, а только те, которые имеют небольшой разброс по энергии. Их концентрация
где
Интерпретация: Выбрали в физическом пространстве области, имеющие определенное выгодное окружение (оптимальный разброс по энергии и расстоянию). Функция
Нужно найти соседа в многомерном пространстве, оптимального и по энергии, и по расстоянию. Примечание: Оказывается в тонких пленках проводимость также может иметь перколяционный характер (через скелет), поскольку их поверхность не сплошная, а островковая.
|

 , т.е. система настолько заморожена, что фононов с необходимой энергии нет. Теперь все определяется температурным слагаемым, но в первом приближении, поскольку e ij разбросаны (из-за флуктуаций) в некоторой полосе, то всегда можно найти какие-то узлы с малым отличием по энергии, пусть и далекие друг от друга (например, с одинаковым окружением заряженных центров). Для таких выделенных центров по-прежнему главным будет не температурное слагаемое
, т.е. система настолько заморожена, что фононов с необходимой энергии нет. Теперь все определяется температурным слагаемым, но в первом приближении, поскольку e ij разбросаны (из-за флуктуаций) в некоторой полосе, то всегда можно найти какие-то узлы с малым отличием по энергии, пусть и далекие друг от друга (например, с одинаковым окружением заряженных центров). Для таких выделенных центров по-прежнему главным будет не температурное слагаемое 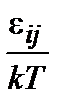 , а
, а 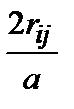 .
.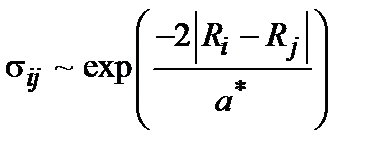 ,
,  ,
, 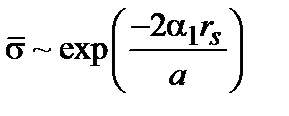 , где
, где 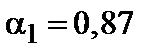 .
.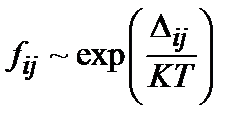 ,
, 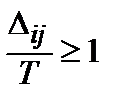 .
.

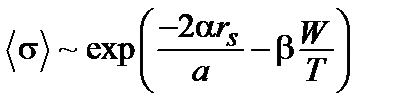 .
.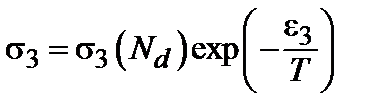 ,
,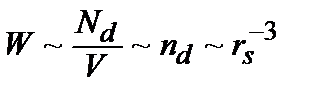 , где
, где 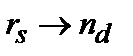 .
.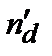 , т.е. выбраны только те примеси, которые удобны.
, т.е. выбраны только те примеси, которые удобны.  . Такие примеси имеют разброс
. Такие примеси имеют разброс  , меньший, чем W:
, меньший, чем W: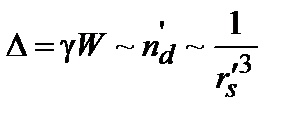 ,
,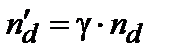 , следовательно
, следовательно 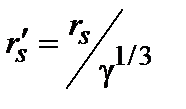 . Т.е. в случае возможности оптимизации по энергетической размазке D, проводимость можно записать в виде
. Т.е. в случае возможности оптимизации по энергетической размазке D, проводимость можно записать в виде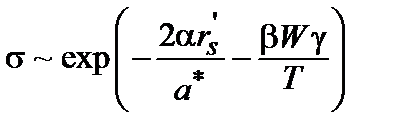 или
или  .
.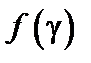 имеет минимум по параметру g
имеет минимум по параметру g
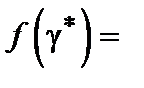

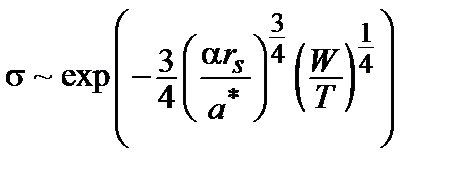 . (8.2)
. (8.2)


