Возбуждения в неупорядоченных системахРассмотрим характерные колебательные, магнитные и электронные возбуждения в таких системах. В описании этих возбуждений имеется много общих математических черт. 1. Фононная система. Пусть, например, конфигурация системы соответствует минимуму потенциальной энергии, причем j -й атом располагается в точке
Здесь В периодической решетке одинаковых атомов силовые постоянные обладают трансляционной симметрией:
Тогда все N уравнений (6.1) становятся эквивалентными, переходя одно в другое при сдвиге решетки. Это свойство симметрии позволяет упростить рассматриваемую систему уравнений с помощью преобразования Фурье. В результате получаются фононные моды кристалла. В неупорядоченных системах, где различные коэффициенты могут быть случайными переменными, такой общей симметрии нет, и уравнение (6.1) надлежит решать другими способами. Простейший пример составляет случай идеального изотопического беспорядка, когда массы
Очевидно, при наличии изотопического беспорядка изменяются лишь диагональные элементы матрицы, соответствующей уравнениям (6.3). Однако в настоящем сплаве «химические» различия между компонентами приводят и к изменению силовых постоянных, что ведет к нарушению условия симметрии (6.2). В этом случае нельзя пренебречь и недиагональным беспорядком. В общем случае (в жидкости или газе) положения равновесия, характеризуемые векторами 2. Магнитная система. Благодаря известной аналогии между фононами и магнонами сразу ясно, что уравнения, описывающие отклонения спинов, можно записать по образцу системы (6.3). Например, для спинового гамильтониана в условиях ферромагнетизма можно записать
Воспользуемся Гейзенберговским представлением и запишем уравнения движения для каждого из операторов спиновых отклонений
в следующем виде:
Если допустить, что все величины
Эта система уравнений аналогична по структуре системе (6.3). 3. Электронная система. Вполне естественно, что похожие уравнения получаются и при описании электронных состояний конденсированной среды в модели сильно связанных электронов. Пусть потенциальная энергия электрона в изолированном j -м атоме есть
Тогда естественно предположить, что решение уравнения Шредингера
можно представить в виде линейной комбинации атомных орбиталей (ЛКАО):
Подставляя разложение (6.8) в уравнение (6.7) и используя свойства атомных орбиталей Для больших систем различные интегралы перекрытия, входящие в эти уравнения, сложны и неопределенны. Они могут быть вычислены из первых принципов только численными методами с использованием принципа минимизации полной энергии системы. Иногда используют упрощенную форму указанных уравнений:
Здесь матричные элементы Итак, можно сказать, что уравнения (6.3, 6.5, 6.9) имеют один и тот же вид:
(здесь a- фиксировано, рассматриваем одну энергетическую зону), где переменная - либо квадрату частоты колебаний -либо энергии h w магнона или экситона, -либо собственному значению энергии E электронного гамильтониана всей системы. Cтатистические характеристики диагональных элементов
Если «исходные» узлы образуют периодическую решетку, то естественно заменить индекс j вектором решетки
Параметр l здесь оказывается собственным значением матрицы в правой части выражения. При рассмотрении колебаний решетки это является обычной динамической матрицей для квадратов частот В простейшей модели металла с сильной связью, когда каждому узлу соответствует один атомный уровень энергии, мы получаем типичную зону разрешенных состояний с энергиями
Если «интеграл перекрытия»
где В – ширина зоны. Энергия электрона в зоне достигает минимума и максимумов соответственно в центре (q = 0) и на границах зоны Бриллюэна. Параметр В удобно использовать в качестве энергетического масштаба системы: он характеризует величину взаимодействия между соседними узлами решетки. Разумеется, сделанные замечания совершенно тривиальны с точки зрения обычной физики твердого тела, а модель электронной или фононной зоны, записанная в виде (6.13), очень далека от настоящих систем. Однако в теории неупорядоченных систем зачастую только такие простые модели и удается рассматривать с известным успехом.
|

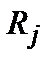 . Как и в обычной теории колебаний решетки, допустим, что при малом смещении этого атома
. Как и в обычной теории колебаний решетки, допустим, что при малом смещении этого атома 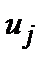 возникают возвращающие силы, линейные по относительным смещениям соседних атомов. Тогда классические уравнения движения для таких смещений запишутся в виде:
возникают возвращающие силы, линейные по относительным смещениям соседних атомов. Тогда классические уравнения движения для таких смещений запишутся в виде: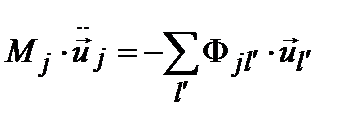 . (6.1)
. (6.1)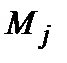 есть масса j -ого атома, тензор
есть масса j -ого атома, тензор 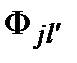 описывает силы, возникающие в узле
описывает силы, возникающие в узле 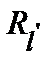 .
.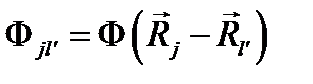 . (6.2)
. (6.2)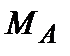 и
и 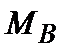 распределены в правильной решетке случайным образом. Интересуясь в основном спектром нормальных колебаний, допустим, что все смещения
распределены в правильной решетке случайным образом. Интересуясь в основном спектром нормальных колебаний, допустим, что все смещения 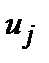 изменяются во времени с одной и той же частотой w. Тогда систему (6.1) можно переписать в виде
изменяются во времени с одной и той же частотой w. Тогда систему (6.1) можно переписать в виде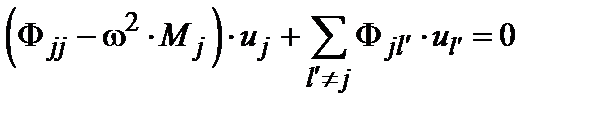 . (6.3)
. (6.3) суть случайные величины, но даже само понятие «близости» узла j к данному узлу l можно определить лишь статистически. Именно поэтому так трудно построить теорию возбуждений в топологически неупорядоченных системах.
суть случайные величины, но даже само понятие «близости» узла j к данному узлу l можно определить лишь статистически. Именно поэтому так трудно построить теорию возбуждений в топологически неупорядоченных системах.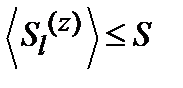 . (6.4)
. (6.4)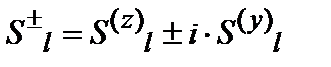
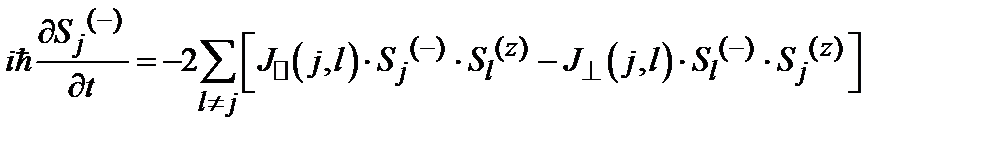 .
.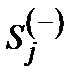 изменяются с одинаковой частотой w и что система почти упорядочена (условие 6.4), то мы придем к системе уравнений
изменяются с одинаковой частотой w и что система почти упорядочена (условие 6.4), то мы придем к системе уравнений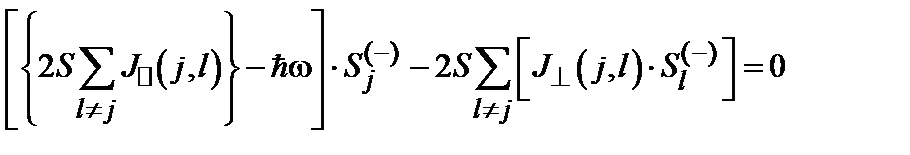 .(6.5)
.(6.5)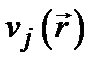 . В этом поле существуют атомные уровни энергии
. В этом поле существуют атомные уровни энергии 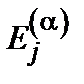 , которым соответствуют различные атомные орбитали
, которым соответствуют различные атомные орбитали 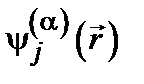 . Допустим далее, что потенциальная энергия электрона в рассматриваемой системе дается просто суммой энергий, которыми он обладал бы в системе отдельных атомах:
. Допустим далее, что потенциальная энергия электрона в рассматриваемой системе дается просто суммой энергий, которыми он обладал бы в системе отдельных атомах: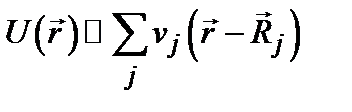 . (6.6)
. (6.6)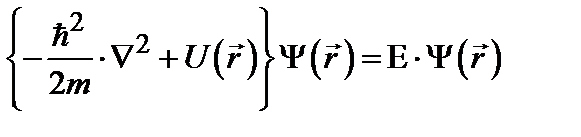 (6.7)
(6.7)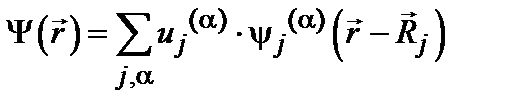 . (6.8)
. (6.8)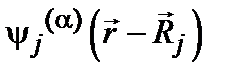 (ортогональность и нормированность), получаем систему линейных уравнений для определения коэффициентов u.
(ортогональность и нормированность), получаем систему линейных уравнений для определения коэффициентов u.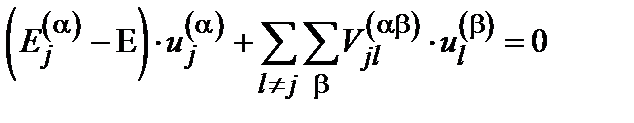 . (6.9)
. (6.9) модельного гамильтониана подбираются эмпирически с таким расчетом, чтобы воспроизвести структуру электронных зон в данном кристалле. Отметим еще раз близкую аналогию между полученными уравнениями и системой (6.3).
модельного гамильтониана подбираются эмпирически с таким расчетом, чтобы воспроизвести структуру электронных зон в данном кристалле. Отметим еще раз близкую аналогию между полученными уравнениями и системой (6.3).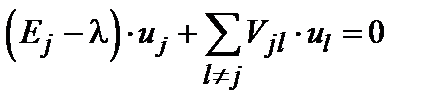 (6.10)
(6.10)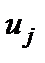 соответствует амплитуде возбуждения на j -м узле, а переменная l, характеризующая спектр возбуждений, соответствует:
соответствует амплитуде возбуждения на j -м узле, а переменная l, характеризующая спектр возбуждений, соответствует: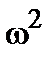 ,
,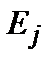 и недиагональных элементов
и недиагональных элементов  можно установить, сопоставляя системы уравнений (6.3), (6.5) или (6.9). В задаче о колебаниях решетки такое сопоставление дает
можно установить, сопоставляя системы уравнений (6.3), (6.5) или (6.9). В задаче о колебаниях решетки такое сопоставление дает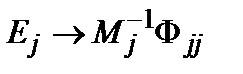 ,
, 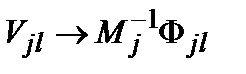 . (6.11)
. (6.11)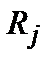 . В упорядоченной системе энергия
. В упорядоченной системе энергия 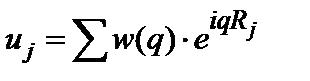 . Совершив преобразования Фурье, получим:
. Совершив преобразования Фурье, получим: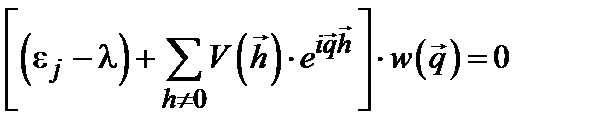 . (6.12)
. (6.12)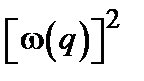 нормальных колебаний с волновым вектором q.
нормальных колебаний с волновым вектором q.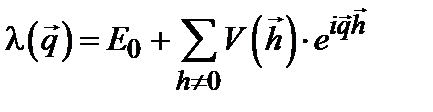 . (6.13)
. (6.13) отличен от нуля лишь для ближайших z соседей данного узла (он тогда равен V), то центру зоны соответствует энергия
отличен от нуля лишь для ближайших z соседей данного узла (он тогда равен V), то центру зоны соответствует энергия 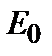 , а полная ширина зоны дается выражением
, а полная ширина зоны дается выражением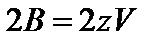 , (6.14)
, (6.14)


