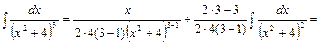Интегрирование по частямПусть
Данная формула называется формулой интегрирования по частям. Эта формула применяется чаще всего к интегрированию выражений, которые можно представить в виде произведения двух сомножителей Основные виды интегралов, которые берутся по частям: Таблица 2
Пример 10. Найти интеграл Решение.
Пример11. Найти интеграл Решение.
Пример12. Найти интеграл Решение.
Получили интеграл первоначального вида. Преобразуем
Из данного равенства выразим искомый интеграл
отсюда
Интегралы такого вида называются круговыми. Пример 13. Найти интеграл Решение.
Пример 14. Найти интеграл Решение.
Некоторые другие виды интегралов также можно находить интегрированием по частям. С помощью формулы интегрирования по частям можно найти интеграл вида
В результате применения метода интегрирования по частям, получили интеграл, в котором подынтегральная функция имеет степень, меньшую на единицу, чем в исходном интеграле:
Данная формула называется рекуррентной формулой. Ее применяют до тех пор, пока не получат табличный интеграл вида Пример 15. Найти интеграл Решение. Применим к данному интегралу рекуррентную формулу:
|

 и
и  – дифференцируемые функции. Известно, что дифференциал произведения
– дифференцируемые функции. Известно, что дифференциал произведения  вычисляется по формуле:
вычисляется по формуле:  . Проинтегрируем данное равенство
. Проинтегрируем данное равенство  . Используя свойства интеграла, будем иметь
. Используя свойства интеграла, будем иметь  , отсюда
, отсюда .
. и
и  , причем за
, причем за  – многочлен степени
– многочлен степени  (см. таблицу 2).
(см. таблицу 2).















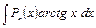








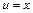









 .
.

 тогда
тогда 
 ,
, 


 .
.
 ,
,  , тогда
, тогда  ,
, 

 .
. тогда
тогда  ,
, 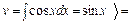



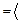 Получили интеграл такого же вида. Еще раз необходимо применить интегрирование по частям:
Получили интеграл такого же вида. Еще раз необходимо применить интегрирование по частям:  ,
,  , тогда
, тогда ,
, 

 .
. ,
, .
. .
. тогда
тогда  ,
, 

 .
.
 тогда
тогда  ,
,





 .
. . Рассмотрим данный интеграл
. Рассмотрим данный интеграл Разобьем на два интеграла
Разобьем на два интеграла 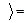

 Первый интеграл оставим без изменений, а во втором интеграле
Первый интеграл оставим без изменений, а во втором интеграле  ,
,  , тогда
, тогда 





 . (1)
. (1) .
. .
. ,
,  .
.