Теорема 6. Уравнение  (7) при условии
(7) при условии  является общим уравнением плоскости.
является общим уравнением плоскости.
Доказательство. Пусть задано уравнение (7). Условие  означает, что хотя бы одно из чисел
означает, что хотя бы одно из чисел  отличен от 0. Роль этих коэффициентов симметрична, поэтому для определенности будем считать, что
отличен от 0. Роль этих коэффициентов симметрична, поэтому для определенности будем считать, что  . Следовательно, при выполнении условия (7) выполняется условие
. Следовательно, при выполнении условия (7) выполняется условие  . Возьмем произвольные 2 числа
. Возьмем произвольные 2 числа  и
и  , и вычислим
, и вычислим  . Следовательно, для точки
. Следовательно, для точки  выполнено соотношение
выполнено соотношение  . Вычитая это соотношение из уравнения (7), получим
. Вычитая это соотношение из уравнения (7), получим  (8)
(8)
Что означает уравнение (8), равносильное уравнению (7)? Оно означает, что скалярное произведение вектора 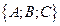 на вектор
на вектор  равно 0, т. е. эти векторы взаимно перпендикулярны. Следовательно, ГМТ уравнений (7) и (8) является плоскость, проходящая через точку
равно 0, т. е. эти векторы взаимно перпендикулярны. Следовательно, ГМТ уравнений (7) и (8) является плоскость, проходящая через точку  перпендикулярно вектору
перпендикулярно вектору 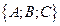 . По сути, вектор
. По сути, вектор 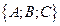 определяет направление плоскости в пространстве. Угол между перпендикулярами к двум плоскостям определяет угол между этими плоскостями.
определяет направление плоскости в пространстве. Угол между перпендикулярами к двум плоскостям определяет угол между этими плоскостями.
Теория прямой на плоскости и теория плоскости в пространстве во многом перекликаются.
Уравнение (8) называется приведенным уравнением плоскости. Оно является общим уравнением плоскости, проходящей через заданную точку перпендикулярно заданному вектору.
Кроме уравнений (7) и (8), в конкретных ситуациях удобно использовать и другие виды уравнения плоскости в пространстве.
Уравнение  (9) называется уравнением плоскости в отрезках. Уравнение (9) является уравнением плоскости, проходящей через точку
(9) называется уравнением плоскости в отрезках. Уравнение (9) является уравнением плоскости, проходящей через точку  на оси абсцисс, через точку
на оси абсцисс, через точку  на оси ординат и через точку
на оси ординат и через точку  на оси аппликат.
на оси аппликат.
Проверьте, что уравнение  (10) является уравнением плоскости, проходящей через 3 заданные точки
(10) является уравнением плоскости, проходящей через 3 заданные точки  ,
,  ,
,  , не лежащие на одной прямой.
, не лежащие на одной прямой.
Аналогично, уравнение  (11) является уравнением плоскости, проходящей через 2 заданные точки
(11) является уравнением плоскости, проходящей через 2 заданные точки  ,
,  параллельно вектору
параллельно вектору  , не коллинеарному вектору
, не коллинеарному вектору  .
.
Также уравнение 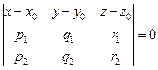 (12) является уравнением плоскости, проходящей через заданную точки
(12) является уравнением плоскости, проходящей через заданную точки  параллельно двум не коллинеарным векторам
параллельно двум не коллинеарным векторам  и
и  .
.
Уравнение 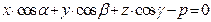 (
( ,
,  ) (13) называется нормированным уравнением плоскости. Уравнение (13) является уравнением плоскости, удаленной на расстояние
) (13) называется нормированным уравнением плоскости. Уравнение (13) является уравнением плоскости, удаленной на расстояние  от начала координат.
от начала координат.
При решении задач используется наиболее удобный вид уравнения плоскости.

 (7) при условии
(7) при условии  является общим уравнением плоскости.
является общим уравнением плоскости. отличен от 0. Роль этих коэффициентов симметрична, поэтому для определенности будем считать, что
отличен от 0. Роль этих коэффициентов симметрична, поэтому для определенности будем считать, что  . Следовательно, при выполнении условия (7) выполняется условие
. Следовательно, при выполнении условия (7) выполняется условие  . Возьмем произвольные 2 числа
. Возьмем произвольные 2 числа  и
и  , и вычислим
, и вычислим  . Следовательно, для точки
. Следовательно, для точки  выполнено соотношение
выполнено соотношение  . Вычитая это соотношение из уравнения (7), получим
. Вычитая это соотношение из уравнения (7), получим  (8)
(8)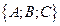 на вектор
на вектор  равно 0, т. е. эти векторы взаимно перпендикулярны. Следовательно, ГМТ уравнений (7) и (8) является плоскость, проходящая через точку
равно 0, т. е. эти векторы взаимно перпендикулярны. Следовательно, ГМТ уравнений (7) и (8) является плоскость, проходящая через точку  (9) называется уравнением плоскости в отрезках. Уравнение (9) является уравнением плоскости, проходящей через точку
(9) называется уравнением плоскости в отрезках. Уравнение (9) является уравнением плоскости, проходящей через точку  на оси абсцисс, через точку
на оси абсцисс, через точку  на оси ординат и через точку
на оси ординат и через точку  на оси аппликат.
на оси аппликат. (10) является уравнением плоскости, проходящей через 3 заданные точки
(10) является уравнением плоскости, проходящей через 3 заданные точки  ,
,  ,
,  , не лежащие на одной прямой.
, не лежащие на одной прямой. (11) является уравнением плоскости, проходящей через 2 заданные точки
(11) является уравнением плоскости, проходящей через 2 заданные точки  , не коллинеарному вектору
, не коллинеарному вектору  .
.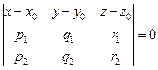 (12) является уравнением плоскости, проходящей через заданную точки
(12) является уравнением плоскости, проходящей через заданную точки  и
и 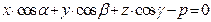 (
( ,
,  ) (13) называется нормированным уравнением плоскости. Уравнение (13) является уравнением плоскости, удаленной на расстояние
) (13) называется нормированным уравнением плоскости. Уравнение (13) является уравнением плоскости, удаленной на расстояние  от начала координат.
от начала координат.


