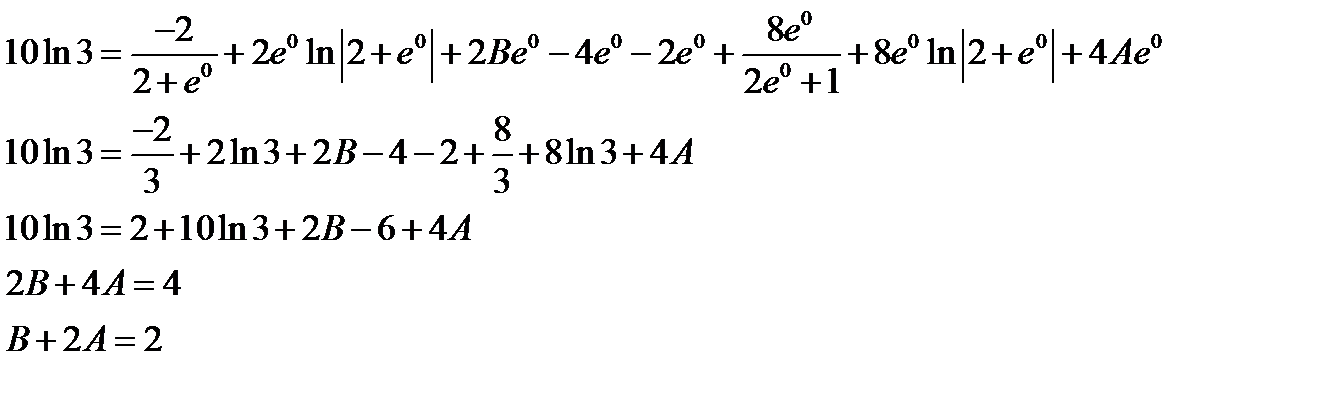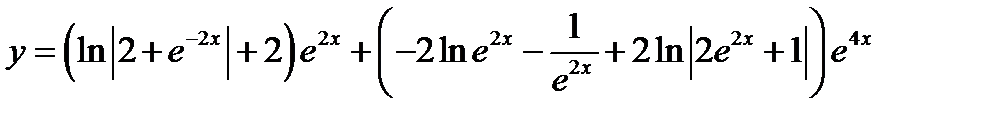Дифференциальные уравнения
Задача 1. Найти общий интеграл дифференциального уравнения Решение:
Отсюда
Задача 2. Найти общий интеграл дифференциального уравнения Решение: Произведем замену переменной
Отсюда
Так как
Задача 3. Найти общий интеграл дифференциального уравнения Решение: Найдем точку пересечения прямых
Отсюда Перенесем начало координат в точку пересечения Таким образом получим
Данное уравнение однородное, поэтому сделаем замену
Отсюда
Таким образом
Сделаем обратную замену
Задача 4. Найти решение задачи Коши
Решение: Дифференциальное уравнение является линейным. Сначала решаем уравнение
В исходном уравнении
Таким образом Так как
Задача 5. Решить задачу Коши
Решение: Преобразуем данное уравнение, имея ввиду, что
Получившееся уравнение является линейным. Сначала решаем уравнение
В уравнении
Решаем интегралы методом интегрирования по частям
Получаем
Таким образом
Задача 6. Найти решение задачи Коши
Решение: Преобразуем данное уравнение, умножив обе части на Сделаем замену Получившееся уравнение является линейным. Сначала решаем уравнение
В уравнении
Таким образом
Задача 7. Найти общий интеграл дифференциального уравнения Решение: Проверим, является ли данное ДУ уравнением в полных дифференциалах:
Так как
отсюда
Так как значит общий интеграл дифференциального уравнения будет равен
Задача 10. Найти общее решение дифференциального уравнения Решение: Сделаем замену переменной Таким образом
Значит
Отсюда
Таким образом
Задача 11. Найти решение задачи Коши
Решение: Произведем замену переменной Таким образом
Значит
Так как Таким образом
Так как Значит
Задача 12. Найти общее решение дифференциального уравнения Решение: Данное дифференциальное уравнение является линейным неоднородным. Сначала найдем общее решение однородного уравнения с помощью характеристического уравнения
Отсюда общее решение однородного уравнения будет выглядеть как
Частное решение будем искать в виде Отсюда
Подставим найденные значения в исходное уравнение
Тогда общее решение исходного линейного неоднородного дифференциального уравнения будет
Задача 13. Найти общее решение дифференциального уравнения Решение: Данное дифференциальное уравнение является линейным неоднородным. Сначала найдем общее решение однородного уравнения с помощью характеристического уравнения
Отсюда общее решение однородного уравнения будет выглядеть как
Частное решение будем искать в виде
Подставим найденные значения в исходное уравнение
Частное решение будет равно Тогда общее решение исходного линейного неоднородного дифференциального уравнения будет
Задача 14. Найти общее решение дифференциального уравнения Решение: Данное дифференциальное уравнение является линейным неоднородным. Сначала найдем общее решение однородного уравнения с помощью характеристического уравнения
Отсюда общее решение однородного уравнения будет выглядеть как
Частное решение будем искать в виде
Подставим найденные значения в исходное уравнение
Частное решение будет равно Тогда общее решение исходного линейного неоднородного дифференциального уравнения будет
Задача 15. Найти общее решение дифференциального уравнения Решение: Данное дифференциальное уравнение является линейным неоднородным. Сначала найдем общее решение однородного уравнения с помощью характеристического уравнения
Отсюда общее решение однородного уравнения будет выглядеть как
Найдем частное решение неоднородного уравнения, применив принцип суперпозиции. Разбиваем правую часть на слагаемые:
Найдем частные решения для каждого слагаемого
Ищем решение в виде
Значит
Ищем решение в виде
Значит Согласно принципу суперпозиции частное решение неоднородного уравнения будет равно сумме частных решений для каждого слагаемого: Тогда общее решение исходного линейного неоднородного дифференциального уравнения будет
Задача 16. Найти решение задачи Коши
Решение: Данное дифференциальное уравнение является линейным неоднородным. Сначала найдем общее решение однородного уравнения с помощью характеристического уравнения
Отсюда общее решение однородного уравнения будет выглядеть как
Найдем частное решение неоднородного дифференциального уравнения, используя метод вариации произвольных постоянных
Положим
Подставим полученные значения в исходное уравнение
Таким образом получаем систему уравнений
Выразим
Используя второе уравнение системы, получим
Находим u
Подставим u и v в выражение для y
Отсюда решение задачи Коши будет таким
|

 (ответ представить в виде
(ответ представить в виде 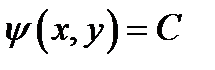 )
)
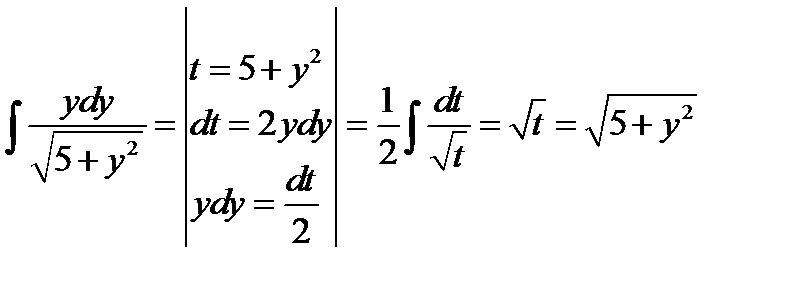
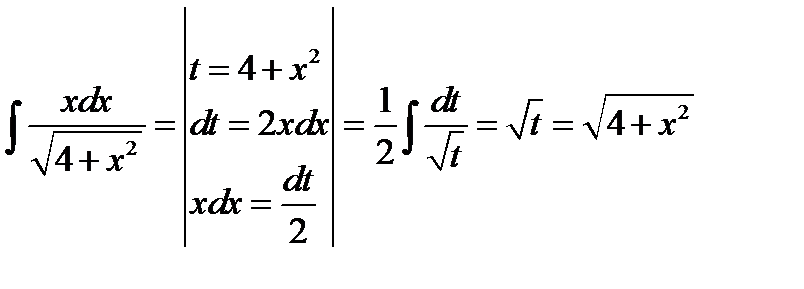

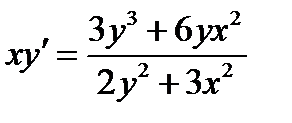

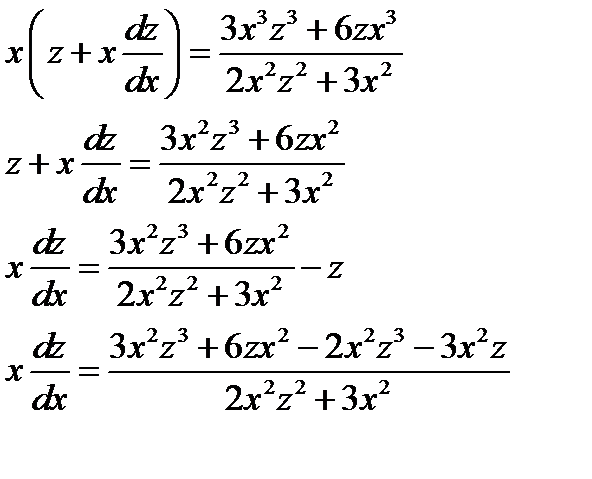



 , то получаем
, то получаем
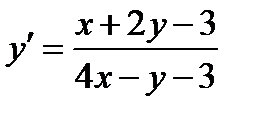
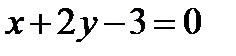 и
и 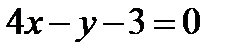 .
.

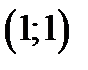 , т.е. сделаем замену
, т.е. сделаем замену 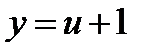 ,
, 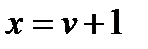

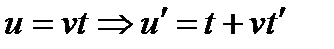



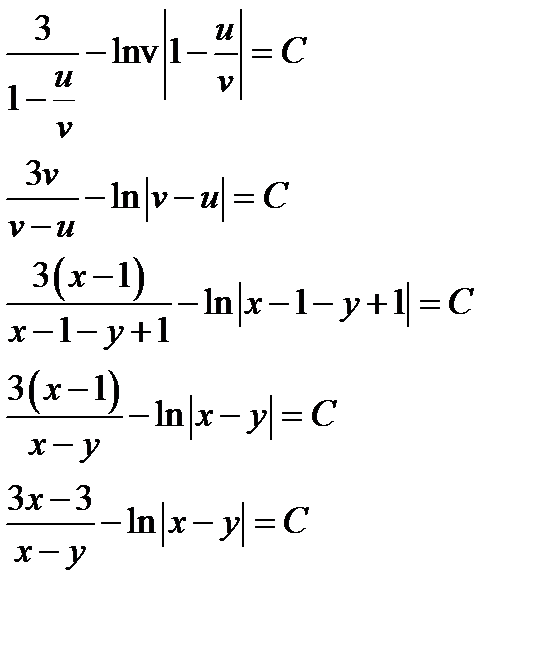
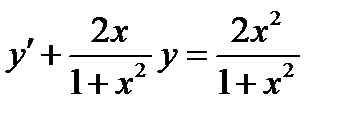 ,
, 

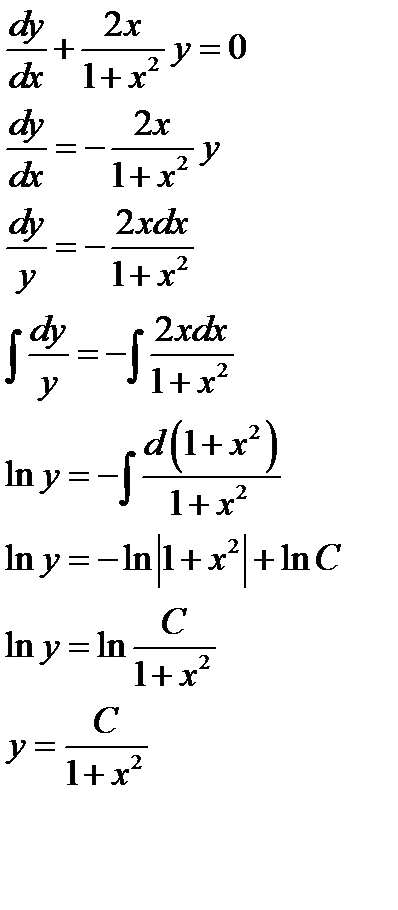
 ,
, 

 общее решение дифференциального уравнения.
общее решение дифференциального уравнения. , поэтому частное решение будет равно
, поэтому частное решение будет равно
 ,
, 
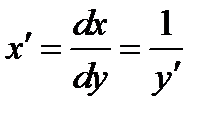 . Таким образом
. Таким образом
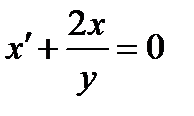

 произведем замену
произведем замену  ,
, 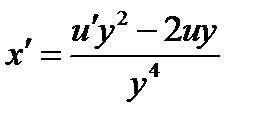

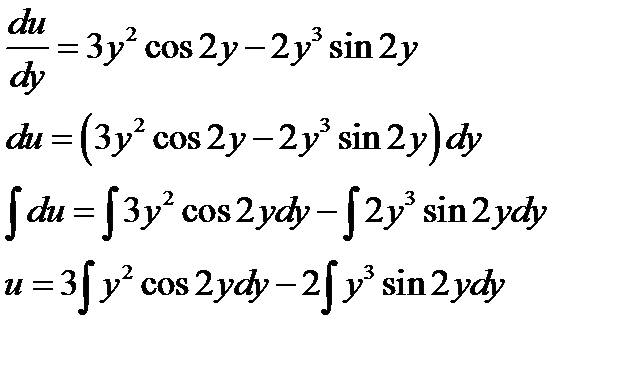
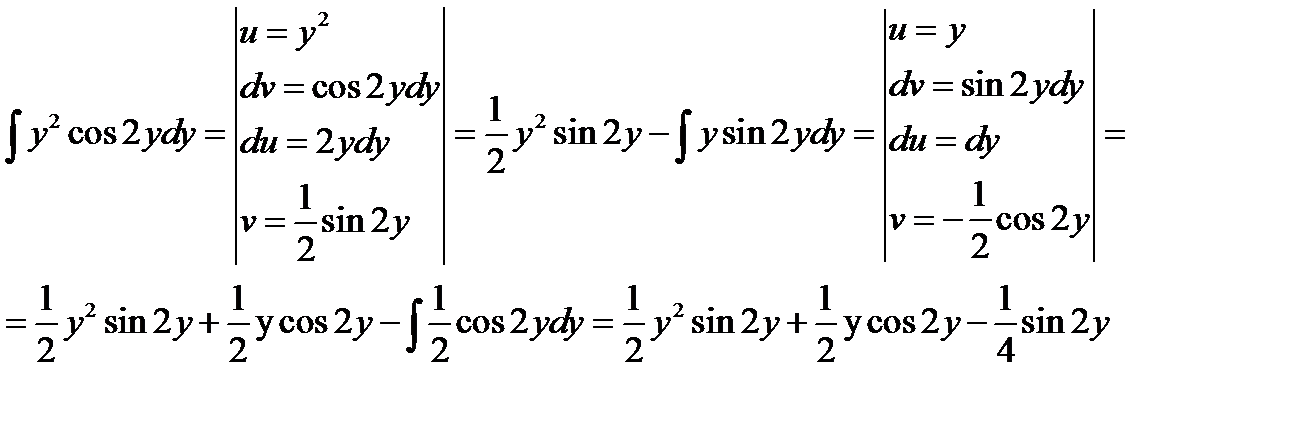
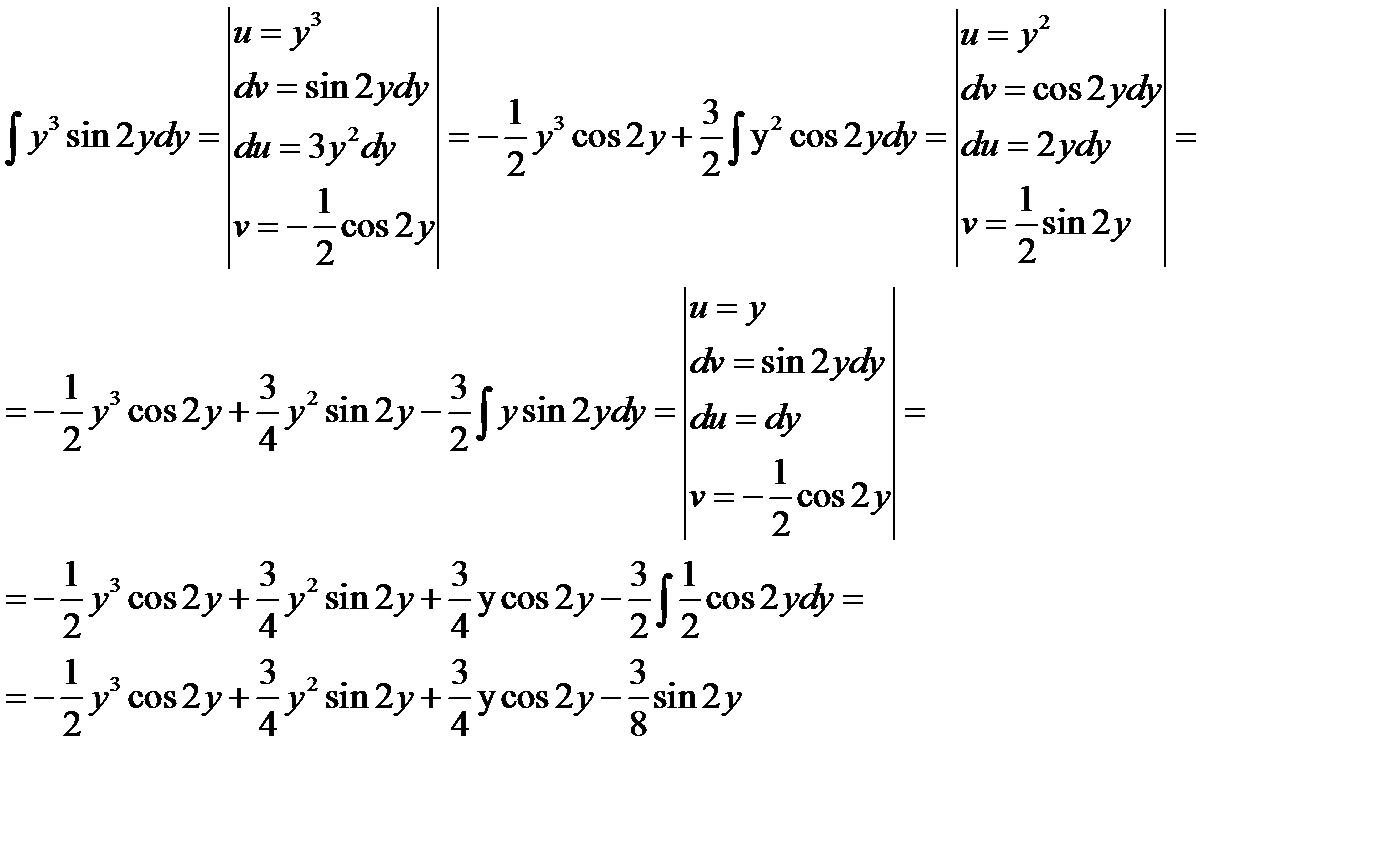

 общее решение дифференциального уравнения. Так как
общее решение дифференциального уравнения. Так как  , то
, то  , поэтому частное решение будет равно
, поэтому частное решение будет равно 
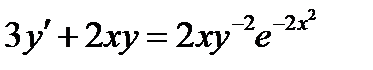 ,
, 
 , получим
, получим  .
. , тогда
, тогда  , получим
, получим 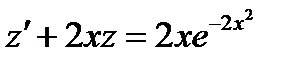 .
.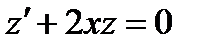


 произведем замену
произведем замену 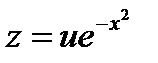 ,
, 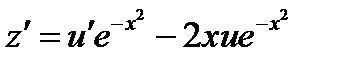

 общее решение дифференциального уравнения. Так как
общее решение дифференциального уравнения. Так как  , то
, то  , поэтому частное решение будет равно
, поэтому частное решение будет равно 

 ,
, 
 ,
, 
 , то уравнение
, то уравнение 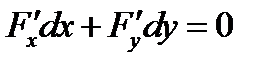
 ,
,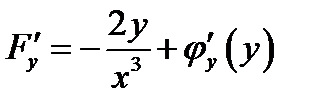
 , то
, то 


 ,
, 

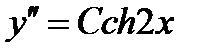
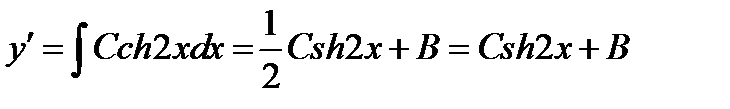

 - общее решение дифференциального уравнения, где C, B, A – произвольные константы.
- общее решение дифференциального уравнения, где C, B, A – произвольные константы.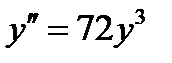 ,
,  ,
, 









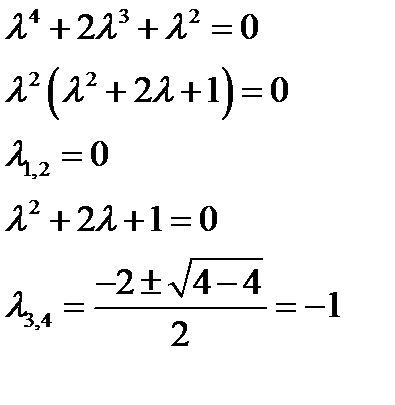
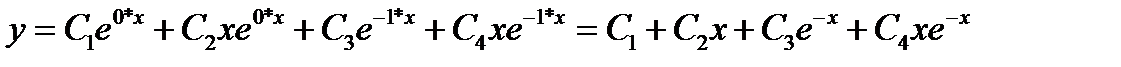


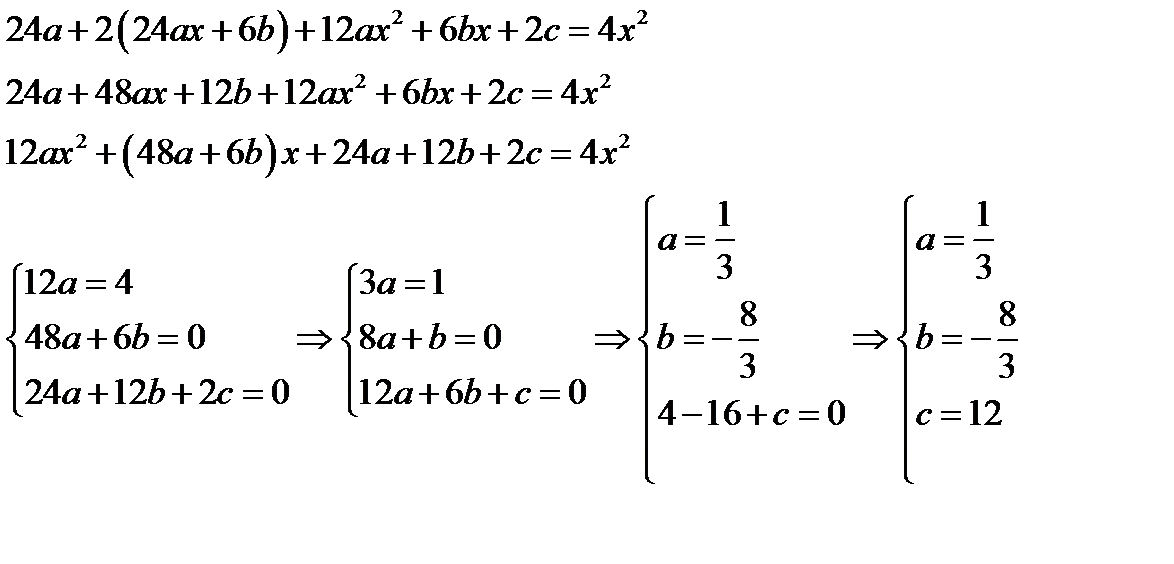












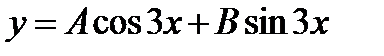
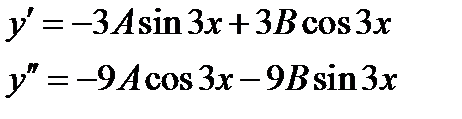










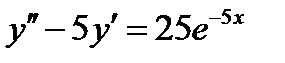






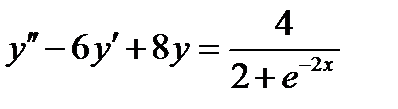 ,
,  ,
, 

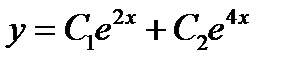

 , тогда
, тогда

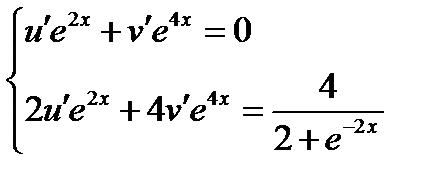
 через
через 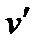 с помощью первого уравнения данной системы
с помощью первого уравнения данной системы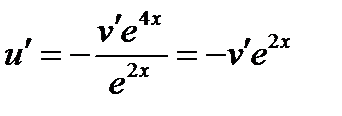
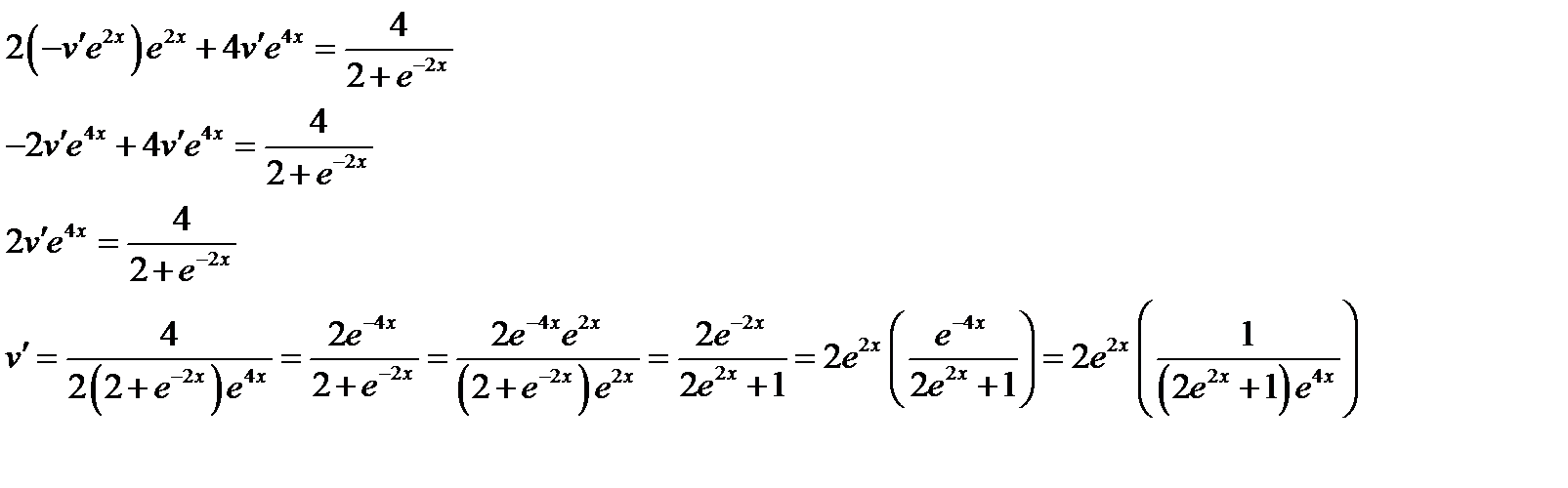



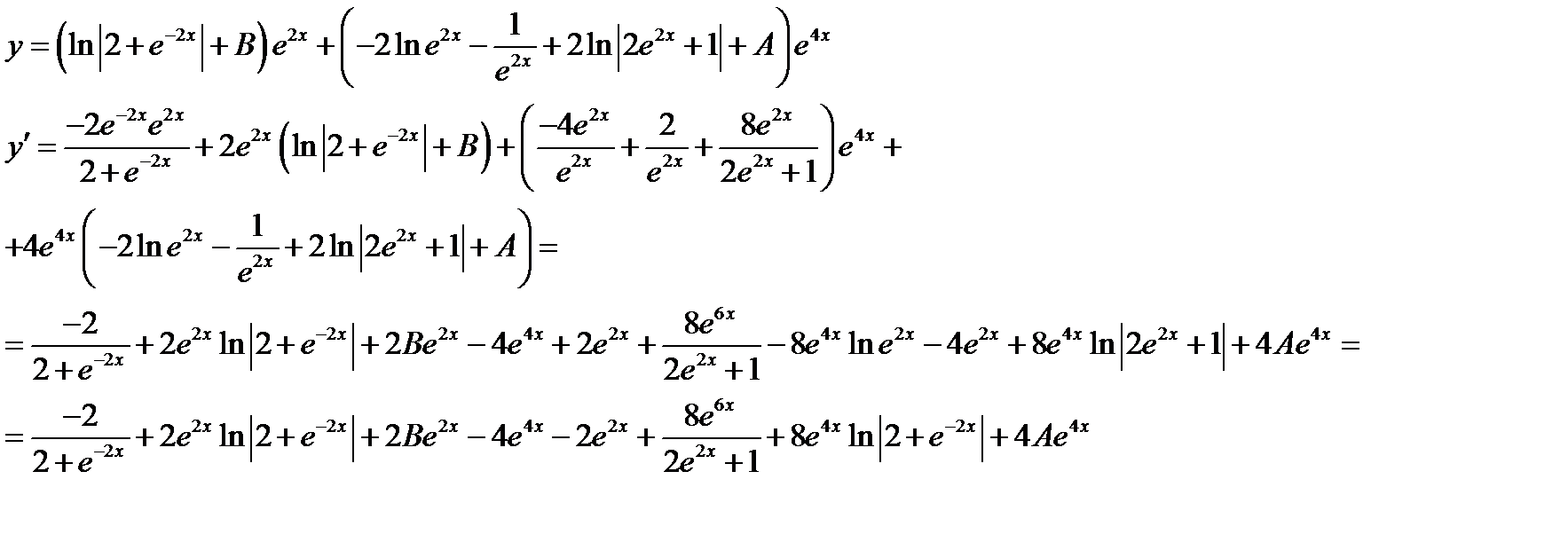 Исходя из начальных условий
Исходя из начальных условий