Непрерывность элементарных функций.1) y = sin x, (-¥ < x < +¥). Ранее мы доказали непрерывность функции sin x в точке x = 0. Докажем непрерывность sin x в произвольной точке а. Для этого нужно доказать, что
sin x - sin a = 2sin Если x ® a, то Рассмотрим теперь функцию у = sin Следовательно, по теореме 3.5, множеством значений данной функции является сегмент Y = [sin(- (рисунок) 2) y = cos x и x = arccos y - доказать непрерывность самостоятельно (рассмотреть y = cos x на [0, p]). 3) y = tg x = Во всех точках области определения tg x является непрерывной функцией как частное двух непрерывных функций. Рассмотрим функцию y = tg x на [- (рисунок) На этом сегменте функция y = tg x - непрерывная и возрастающая (возрастание следует из формулы tg Заметим теперь, " y $d > 0, такое, что y Î [tg(- Так как tg(- (рисунок) 4) y = ctg x и x = arcctg y - доказать непрерывность самостоятельно. 5) y = Эта функция непрерывна в любой точке как произведение n непрерывных функций, равных х. Рассмотрим теперь y = На этом сегменте y = Так как " у > 0 $ a > 0 такое, что у Î [0, Положим по определению Тем самым определена функция y = 6) y = Для рациональных х эта функция определна в пункте 5). Отметим, что для рациональных показателей степени r = 1)
если  > >  , то , то 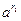 > >  при а > 1, при а > 1,  > > 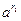 при 0< а < 1. при 0< а < 1.
2) 3) 4) 5) 6) 7) Определим теперь Пусть х - любое вещественное число. Рассмотрим случай, когда a > 1. Рассмотрим множество { Положим по определению: Можно было определить Дома доказать, что Если 0 < a < 1, то Можно показать,что функция ax для любых вещественных х обладает такими же свойствами 1)- 7), как и для рациональных показателей степени. В частности, ax - возрастающая функция при а > 1 и ax убывающая функция при 0 < a < 1. Дкажем теперь непрерывность ax для любого вещественного х. Для определённости рассмотрим случай а > 1, возьмём произвольное х = с и докажем сначала непрерывность ax в точке с слева. Для этого нужно доказать, что " e > 0 $ левая полуокрестность точки с, в которой aс - ax < e. (рисунок) По определению, aс = (рисунок) Так как aх - возрастающая функция, то " х Î { откуда aс - ax < e при Непрерывность aх в точке с слева доказана. Аналогично доказывается непрерывность aх в точке с справа. Из непрерывности в точке с слева и справа следует непрерывность aх в точке с. Рассмотрим теперь функцию у = aх на произвольном сегменте [ b, c ]. На этом сегменте эта функция строго монотонная и непрерывная. Следовательно, по теореме 3.5 множеством значений данной функции является сегмент Y = [ ac, ab ]. На Y существует обратная функция (она обозначается x = log a y), строго монотонная и непрерывная. Так как " y > 0 $ b и c такие, что y Î [ ac, ab ], то функция x = log a y - сторого монотонная и непрерывная на полупрямой (0, +¥). Если а = е, то логарифм называется натуральным и обозначается log е x = ln x, а показательная функция ех называется экспонентой. 7) Степенная функция с произвольным вещественным показателем. у = х a (a - любое вещественное число). Область определения Х = { x > 0}. Так как х a = е aln x = еt, где t = aln x, то у = х a непрерывна в любой точке х > 0 как суперпозиция двух непрерывных функций. Рассмотренные элементарные функции называются основными элементарными функциями. Любая функция, которая получается из основных элементарных функций в результате конечного числа арифметических операций и суперпозиций - называется элементарной функцией, а множество всех элементарных функций называется классом элементарных функций. Из теоремы о непрерывности сложной функции и теоремы об арифметических действиях над непрерывными функциями следует, что любая элементарная функция непрерывна во всякой точке, в окрестности которой она определена. Например, у = (sin x)ln tg x. непрерывна во всех точках x, в которых sin x > 0 и tg x > 0. Рассмотрим функцию y = Х = { x = 2p n, n Î Z }, то есть эта функция определена в точках, которые не являются предельными точками области определения. (рисунок) Поэтому данная функция не является непрерывной в этих точках.
|

 sin x = sin a, или что sin x - sin a ® 0 при x ® a. Воспользуемся формулой
sin x = sin a, или что sin x - sin a ® 0 при x ® a. Воспользуемся формулой cos
cos  .
. , Х =[-
, Х =[-  £ x £
£ x £  - sin
- sin  = 2sin
= 2sin 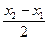 cos
cos 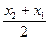 ).
). (x ¹
(x ¹  ).Следовательно, по теореме 3.5 множеством значений данной функции является сегмент Y = [tg(-
).Следовательно, по теореме 3.5 множеством значений данной функции является сегмент Y = [tg(-  , n - натуральное, Х Î (-¥, ¥).
, n - натуральное, Х Î (-¥, ¥). ], на Y существует обратная функция х =
], на Y существует обратная функция х =  =
=  , возрастающая и непрерывная.
, возрастающая и непрерывная. =
=  (" х > 0, любого натурального n и любого целого m).
(" х > 0, любого натурального n и любого целого m). (a > 0, a ¹ 1)
(a > 0, a ¹ 1) функция
функция  обладает следующими свойствами:
обладает следующими свойствами: .
. =
=  .
. =1(по определению).
=1(по определению). =
=  (по определению).
(по определению). =
=  .
. {
{  {
{  }
} > 1. По определнию положим " х: ax =
> 1. По определнию положим " х: ax =  .
. { ar }. Зададим произвольное e > 0 и рассмотрим число aс - e. По определению точной верхней грани найдется рациональное число
{ ar }. Зададим произвольное e > 0 и рассмотрим число aс - e. По определению точной верхней грани найдется рациональное число  < c:
< c:  > aс - e.
> aс - e. , её область определения
, её область определения


