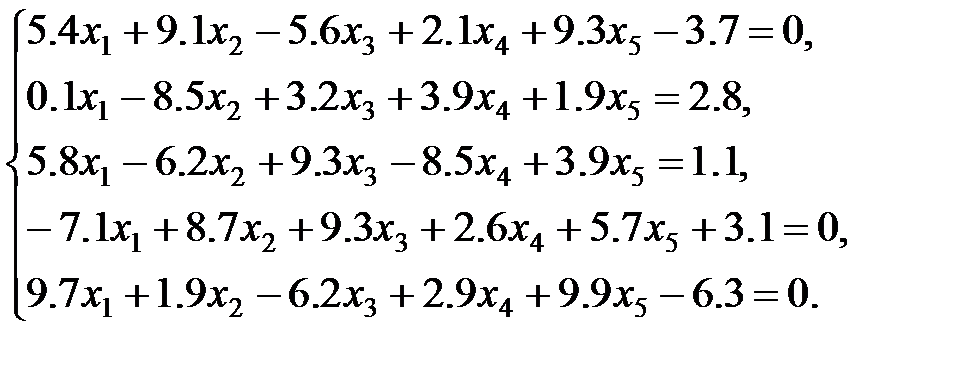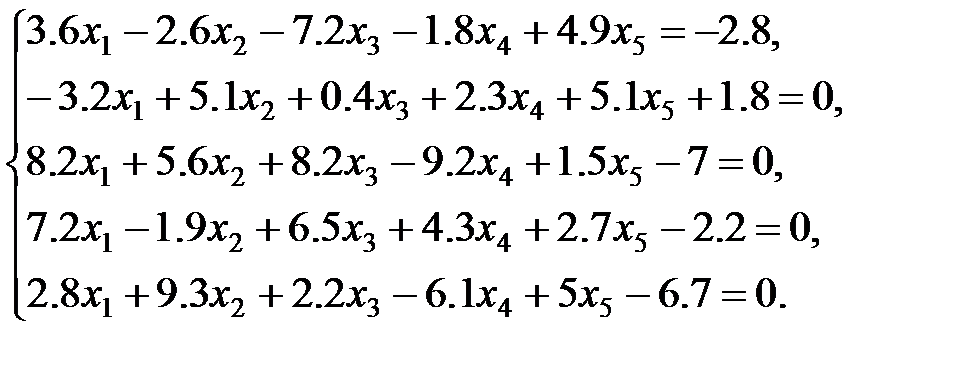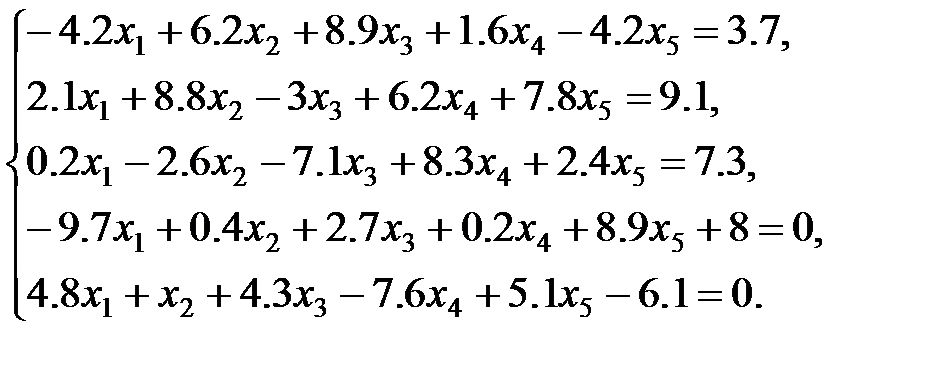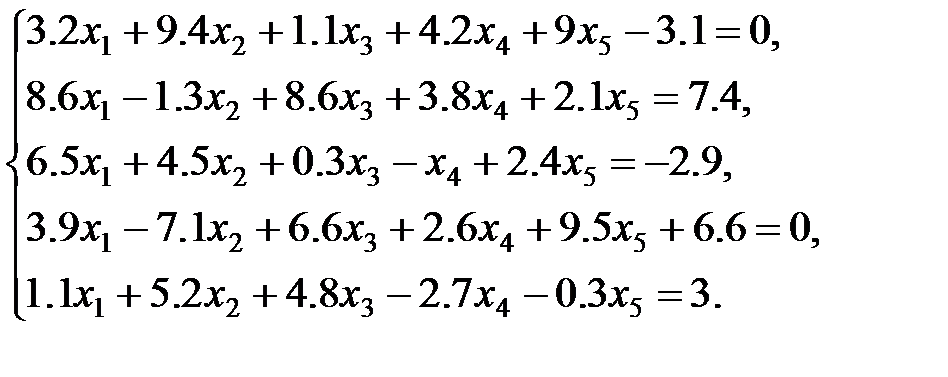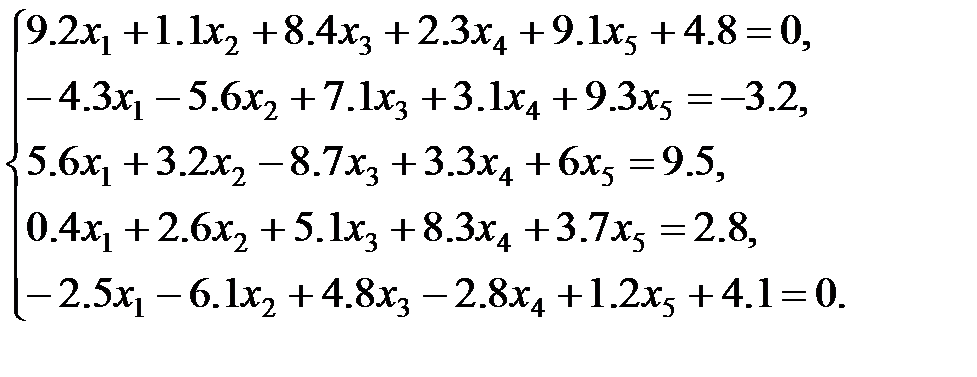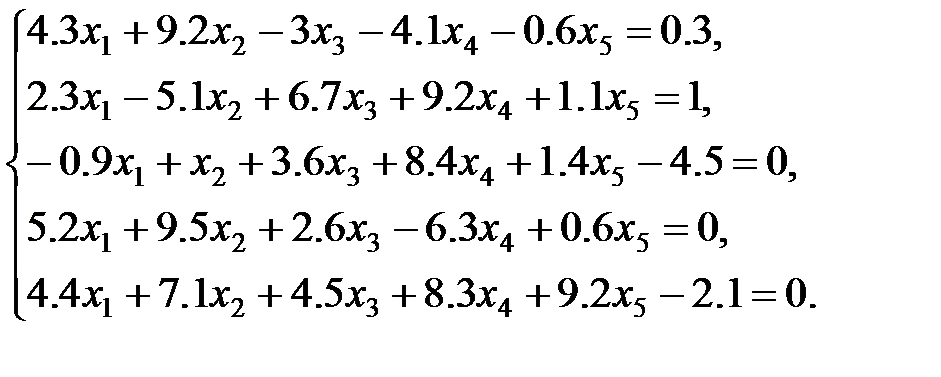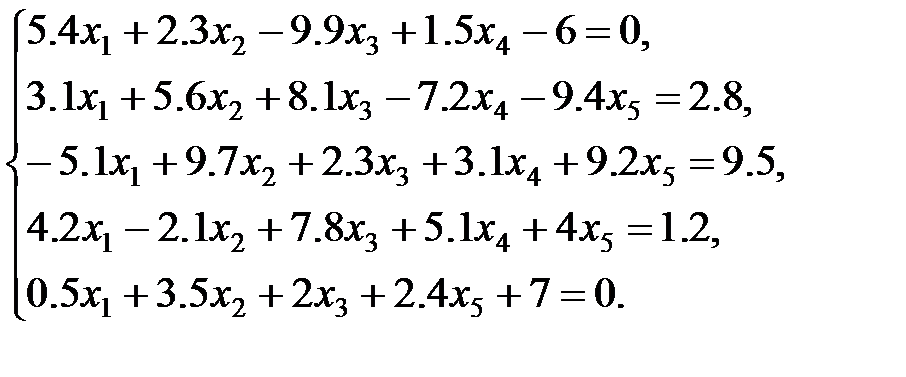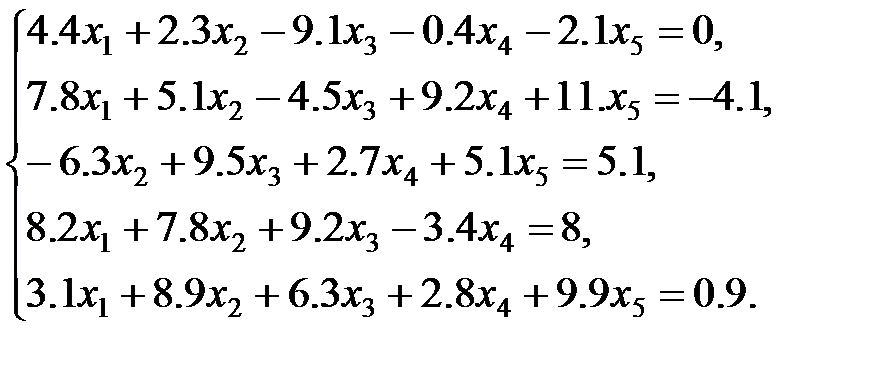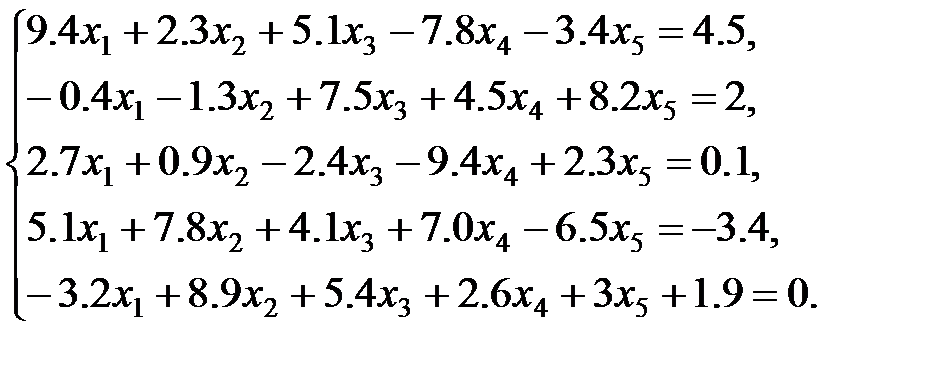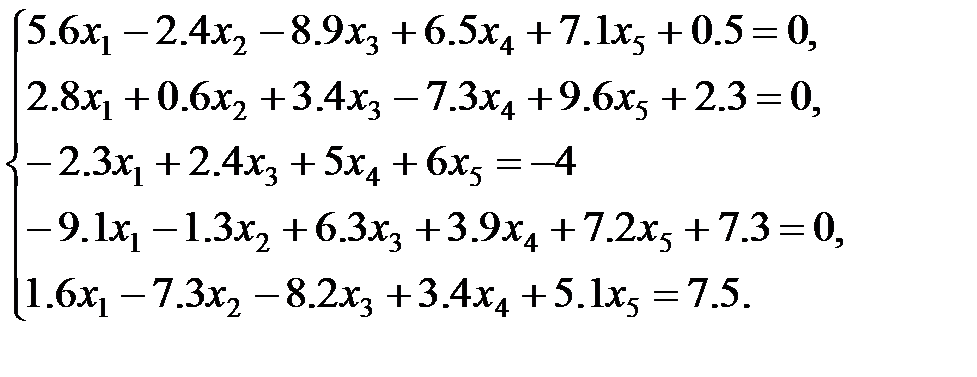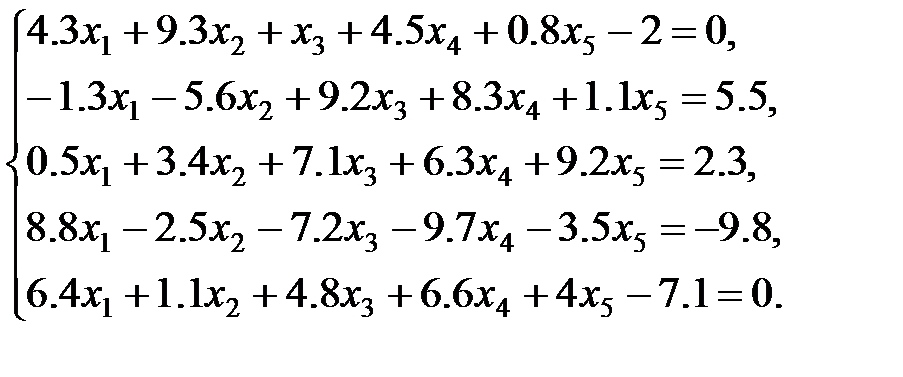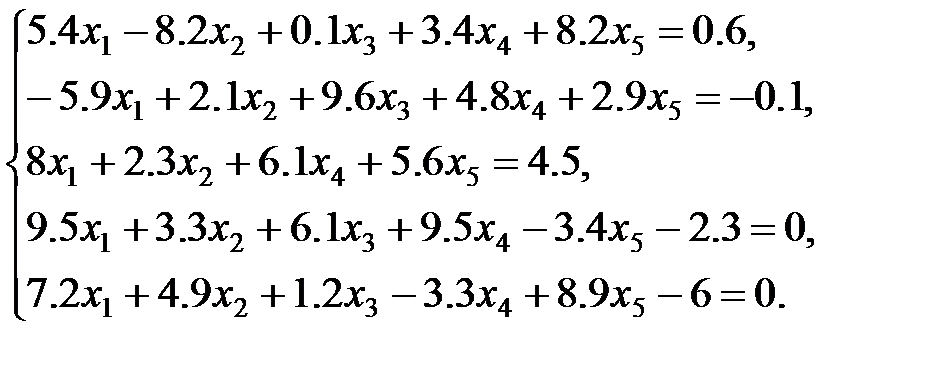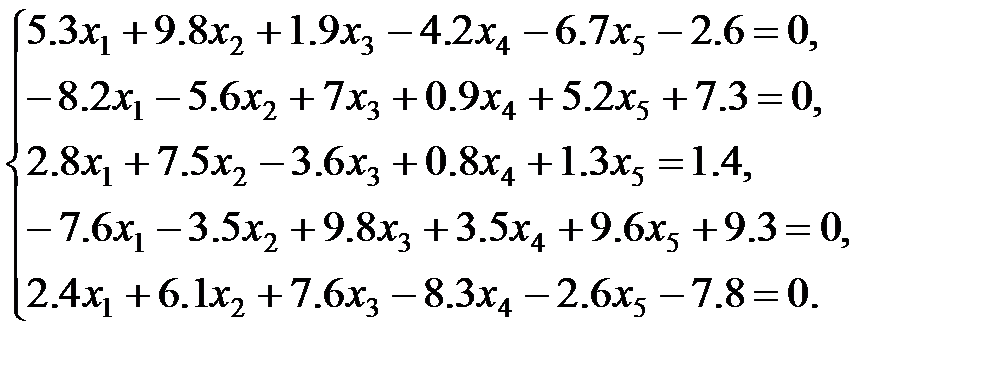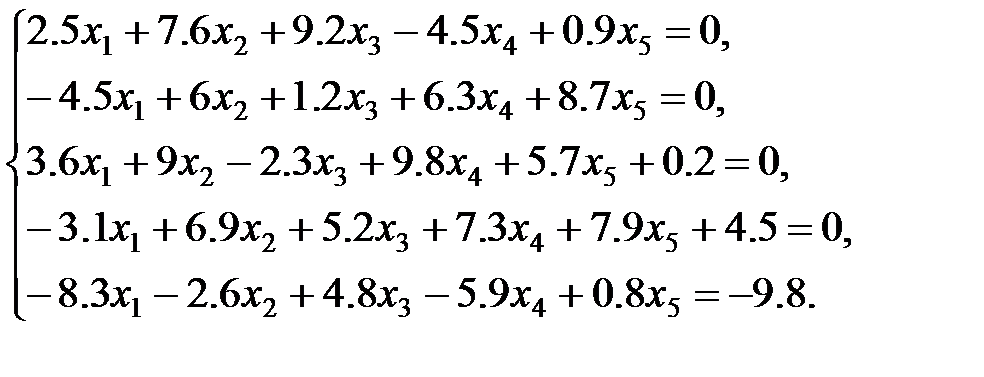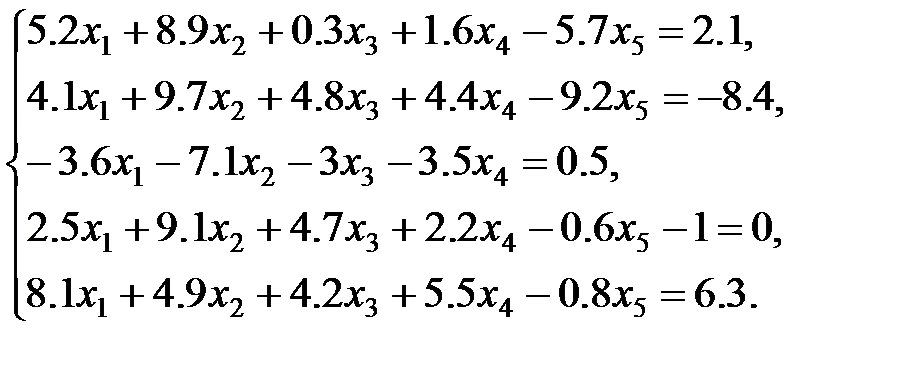Метод LU-разложенияЦель работы: · Знакомство с алгоритмом LU-разложения матрицы коэффициентов; · Применение метода LU-разложения к решению систем линейных уравнений; · Использование возможностей системы MATHCAD для выполнения LU-разложения. Постановка задачи: Найти решение системы линейных уравнений
Описание метода: Метод LU-разложения является одной из разновидностей метода Гаусса и заключается в представлении матрицы коэффициентов A в виде
Доказано, что если главные миноры матрицы A отличны от нуля, то разложение всегда возможно и единственно. При наличии LU-разложения решение системы
Из первого уравнения находим
Затем составляется система
Из последнего уравнения этой системы найдем
Для построения LU-разложения матрицы A создаются последовательно матрицы
и вычисляются матрицы
Последняя матрица Основное преимущество метода LU-разложение заключается в том, что столбец свободных членов при решении системы линейных алгебраических уравнений используется только на заключительном этапе, а наиболее трудоемкие операции по вычислению матриц L и U не требует знания вектора свободных членов b. Таким образом, если решается серия СЛАУ с одной и той же матрицей коэффициентов A, но разными правыми частями b, то очень выгодно один раз вычислить LU-разложение матрицы A, а уже за тем решать конкретные системы, меняя столбец свободных членов. Если матрица A СЛАУ содержит много нулей, то использование LU-разложения может существенно сократить объем вычислений. Можно проверить, что если какая-то строка матрицы A до первого ненулевого элемента содержит m нулей, то та же строка в матрице L будет содержать в начале m нулей. Если какой-то столбец в матрице A содержит до первого ненулевого элемента p нулей, то в матрице U этот столбец в своем начале будет иметь p нулей. Но наряду с достоинствами метод LU-разложения имеет и недостатки. Алгоритм LU-разложения может остановиться даже при невырожденной матрице A из-за деления на нуль при
Ход лабораторной работы: 1. Ввести матрицу коэффициентов A (n × n) и столбец свободных членов b (см. задания для самостоятельной работы). 2. Последовательно создать матрицы 3. Нашли 4. Найти матрицу
Легко проверяется, что
5. Найти решение системы 6. Найти решение системы 7. Выполнить проверку. 1) Для проверки разложения: Вычислить произведение матриц LU, сравнить с исходной матрицей A. 2) Для проверки решения: Посмотреть выполняется ли равенство
Пример: Найти решение системы линейных уравнений
Получим LU-разложение матрицы коэффициентов.
Требования к отчету: 1. Отчет должен быть представлен в электронном виде; 2. Отчет должен содержать: · Расчеты и проверку. · Ответы на вопросы: · Какова точность найденного решения; · Преимущество метода LU-разложения по сравнению с правилом Крамера и использованием обратной матрицы; · В чем заключается различие между методом Гауса и LU-разложением? · Недостатки метода.
Задания для самостоятельной работы: 1 вариант:
2 вариант:
3 вариант:
4 вариант:
5 вариант:
6 вариант:
7 вариант:
8 вариант:
9 вариант:
10 вариант:
11 вариант:
12 вариант:
13 вариант:
14 вариант:
15 вариант:
|

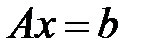 с помощью метода LU-разложения, где
с помощью метода LU-разложения, где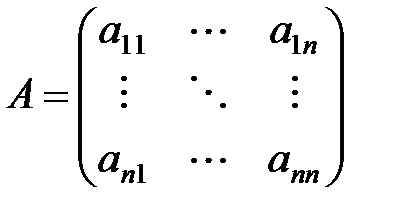 – невырожденная матрица коэффициентов размера
– невырожденная матрица коэффициентов размера 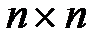 ,
,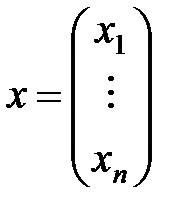 ,
, 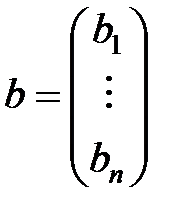 – столбец неизвестных и столбец свободных членов соответственно.
– столбец неизвестных и столбец свободных членов соответственно.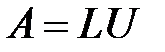 , где L - нижняя треугольная матрица с единицами на диагонали, U - верхняя треугольная матрица.
, где L - нижняя треугольная матрица с единицами на диагонали, U - верхняя треугольная матрица.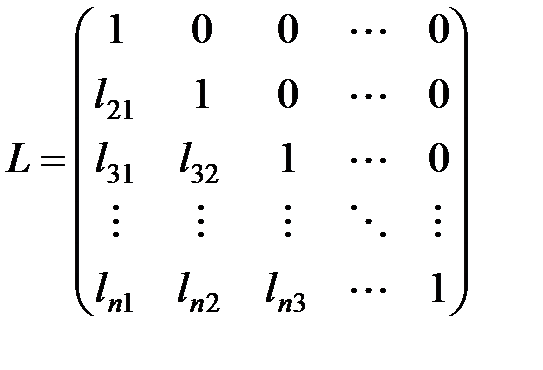
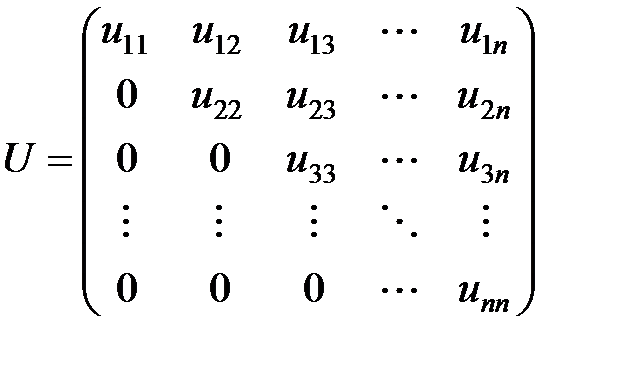
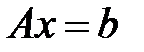 сводится к решению двух систем с треугольной матрицей:
сводится к решению двух систем с треугольной матрицей: 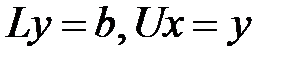 .Первая система имеет вид:
.Первая система имеет вид: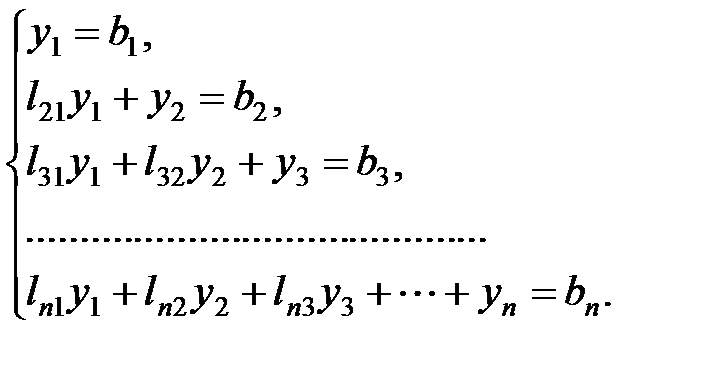
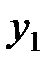 , из второго –
, из второго – 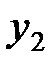 , и т.д. Запишем общую формулу:
, и т.д. Запишем общую формулу: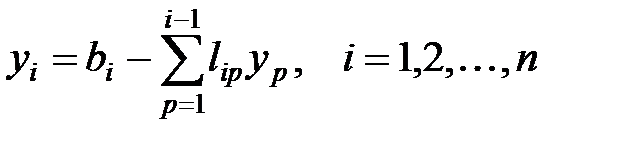 .
.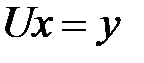 :
: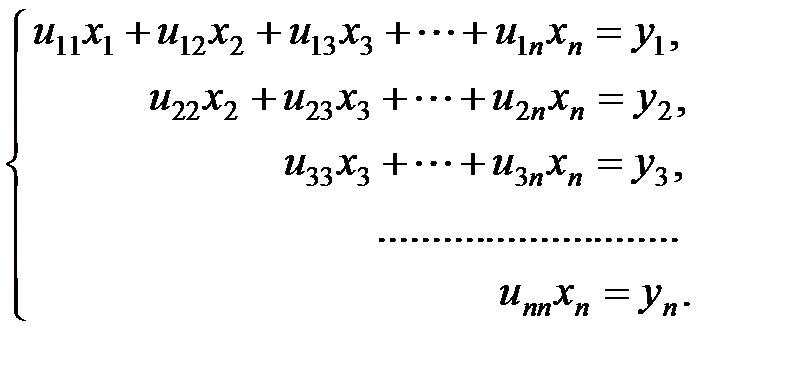
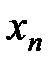 , из предпоследнего –
, из предпоследнего – 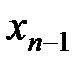 , и т.д. Получим формулу для решения системы
, и т.д. Получим формулу для решения системы 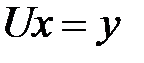 :
: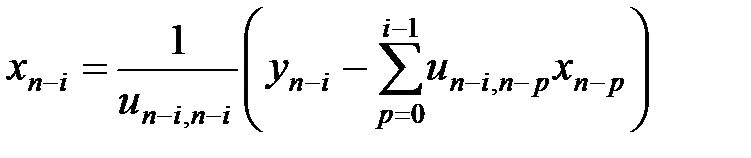 .
.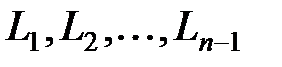 , где
, где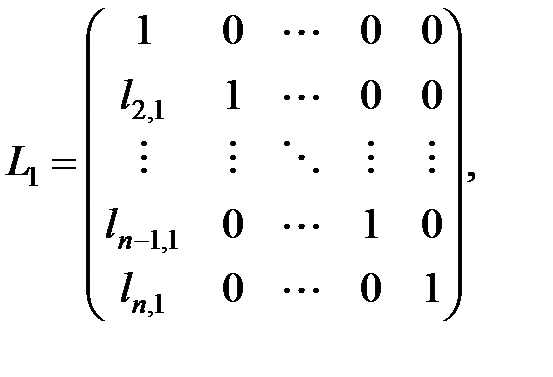
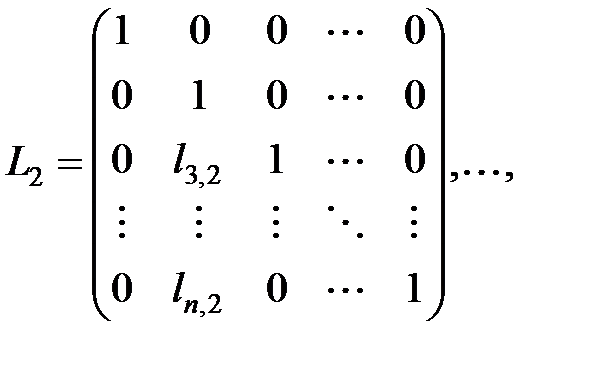

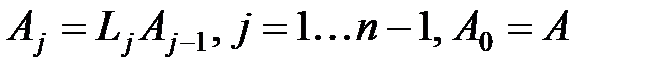 . Легко проверить, что умножение произвольной матрицы М порядка n на
. Легко проверить, что умножение произвольной матрицы М порядка n на 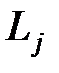 слева означает, что к строке с номером k,
слева означает, что к строке с номером k, 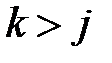 , прибавляется строка с номером j, умноженная на
, прибавляется строка с номером j, умноженная на 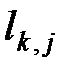 . Умножая матрицу
. Умножая матрицу 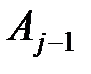 мы добиваемся, чтобы в j- ом столбце матрицы
мы добиваемся, чтобы в j- ом столбце матрицы 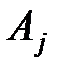 под диагональю стояли нули. Для этого берем
под диагональю стояли нули. Для этого берем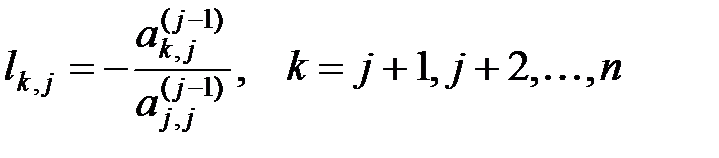 .
.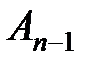 будет верхней треугольной. Она выражается через исходную матрицу
будет верхней треугольной. Она выражается через исходную матрицу 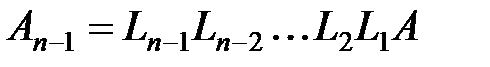 . Пусть
. Пусть 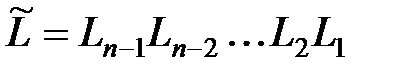 . Тогда
. Тогда 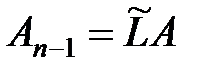 , откуда
, откуда 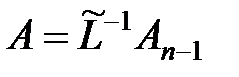 . Пусть
. Пусть 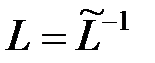 ,
, 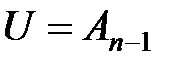 . Так как произведение нижних треугольных матриц дает нижнюю треугольную матрицу и обратная к нижней треугольной матрице будет нижней треугольной, то матрица L – нижняя треугольная. Нужное разложение
. Так как произведение нижних треугольных матриц дает нижнюю треугольную матрицу и обратная к нижней треугольной матрице будет нижней треугольной, то матрица L – нижняя треугольная. Нужное разложение 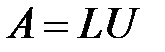 получено.
получено.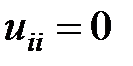 . Кроме того при ненулевом, но малом значении
. Кроме того при ненулевом, но малом значении 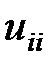 ошибки округлений в результате деления на
ошибки округлений в результате деления на 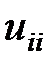 могут сильно возрастать и искажать получаемое решение.
могут сильно возрастать и искажать получаемое решение.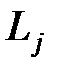 находятся по формулам:
находятся по формулам: 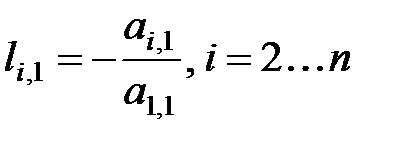 ;
; 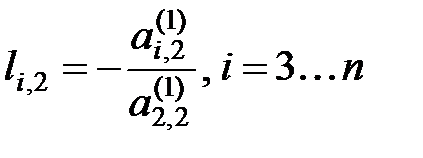 ; …;
; …; 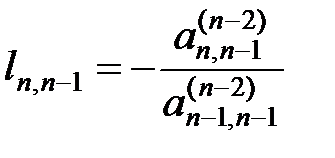 , где верхний индекс j элемента
, где верхний индекс j элемента 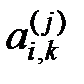 – индекс матрицы
– индекс матрицы 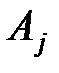 , а нижние индексы i, k – номер строки и номер столбца соответственно.
, а нижние индексы i, k – номер строки и номер столбца соответственно.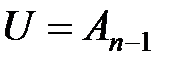 .
.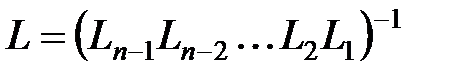 . Заметим, что в действительности обратную матрицу вычислять не приходится. По правилу обращения произведения получим
. Заметим, что в действительности обратную матрицу вычислять не приходится. По правилу обращения произведения получим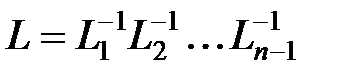 .
.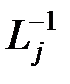 получается из
получается из 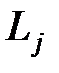 сменой знака у ненулевых элементов j -o столбца, стоящих ниже диагонали. По смыслу умножения на матрицу вида
сменой знака у ненулевых элементов j -o столбца, стоящих ниже диагонали. По смыслу умножения на матрицу вида 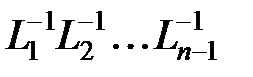 ненулевые элементы матрицы
ненулевые элементы матрицы 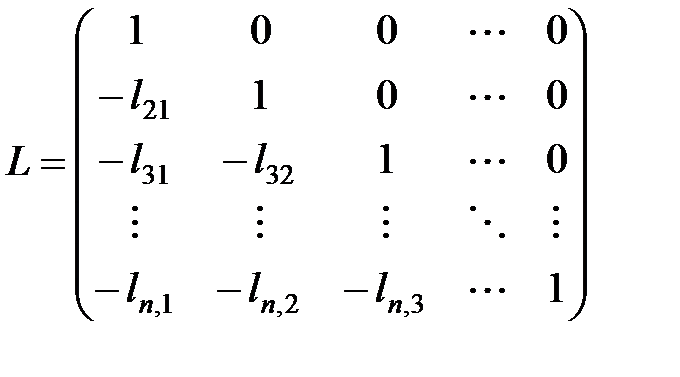
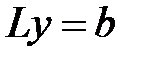 .
.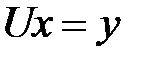 , записать решение исходной системы линейных уравнений.
, записать решение исходной системы линейных уравнений.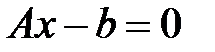 ?
?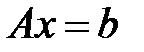 , где
, где
 Создаем единичную матрицу
Создаем единичную матрицу 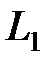 :
:
 Задаем цикл («..» ставится при нажатии «;»):
Задаем цикл («..» ставится при нажатии «;»):
 Находим коэффициенты
Находим коэффициенты 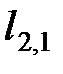 ,
, 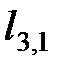 :
:


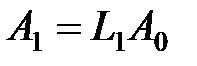 (произведение матриц требует порядка n 3 действий. Оптимальнее, вместо вычисления произведения, присвоить элементам матрицы те, которые не изменяются. Или же новую матрицу можно не создавать, а изменять изначальную), она имеет вид
(произведение матриц требует порядка n 3 действий. Оптимальнее, вместо вычисления произведения, присвоить элементам матрицы те, которые не изменяются. Или же новую матрицу можно не создавать, а изменять изначальную), она имеет вид 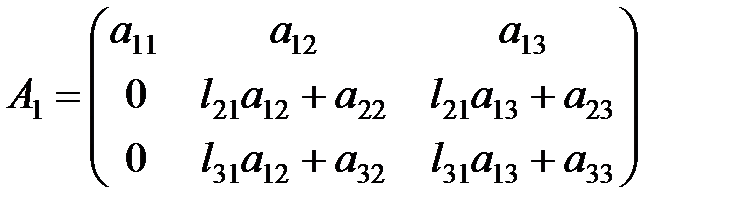 . Выполнили всего порядка n 2 действий:
. Выполнили всего порядка n 2 действий:




















 Разложение найдено верно:
Разложение найдено верно: