1о. Эвристические соображения.
В анализе изучаются дробно-рациональные функции вида 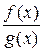 , где
, где 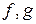 − многочлены. Мы их будем рассматривать как формальные выражения. При этом используем обычные операции:
− многочлены. Мы их будем рассматривать как формальные выражения. При этом используем обычные операции:
 , где
, где 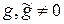 ;
; 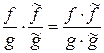 ;
;
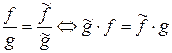 .
.
В этом случае две дроби определяют одну и ту же рациональную функцию.
2о. Точные определения.
Пусть 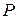 – поле,
– поле,  – кольцо многочленов над
– кольцо многочленов над 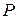 .
.
Определение 1. 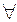 паре многочленов
паре многочленов  , где
, где 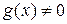 поставим в соответствие символ
поставим в соответствие символ 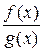 , называемый рациональной дробью с числителем
, называемый рациональной дробью с числителем  и знаменателем
и знаменателем 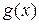 .
.
Замечание. Здесь используется термин «символ», т.к. мы не делим многочлены, хотя и иногда их можно разделить без остатка.
Определение 2. Рациональные дроби 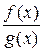 и
и 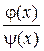 называются равными, если в кольце
называются равными, если в кольце  имеется равенство
имеется равенство
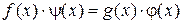 . .
| (1)
|
Свойства рациональных дробей.
1. 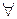 дробь равна самой себе.
дробь равна самой себе.
2. Свойство транзитивности: если  и
и 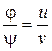
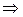
 .
.
Действительно,  ,
, 
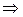
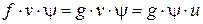 . Далее после деления на
. Далее после деления на  получим доказываемое равенство, т.к.
получим доказываемое равенство, т.к.  – кольцо без делителей нуля.
– кольцо без делителей нуля.
Объединим все равные между собой дроби в один класс. Тогда множество всех рациональных дробей разбивается на непересекающиеся классы равных между собой дробей. На множестве этих классов мы хотим определить операции так, чтобы оно было полем. Для этого надо проверять, что замена представителя класса другим не изменяет результат с точки зрения принадлежности классу.
Лемма 1. Рациональная дробь превращается в равную дробь, если её знаменатель и числитель умножаются или сокращаются на один и тот же многочлен, отличенный от нуля.
Доказательство. Действительно, так как из  и можно разделитьна
и можно разделитьна 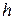 , то получаем, что операция не выводит из класса.■
, то получаем, что операция не выводит из класса.■
Сложение рациональных дробей определим как
\
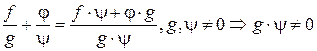
| (2)
|
Далее, если
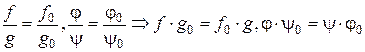 ,
, 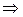 | умножая первое на
| умножая первое на  , а второе на
, а второе на  и складывая |
и складывая | 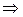

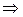
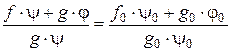
Т.о. если складывать 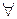 дробь одного класса с
дробь одного класса с 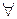 дробью другого класса, то результаты всегда лежат в одном и том же третьем классе. Этот класс называется суммой классов.
дробью другого класса, то результаты всегда лежат в одном и том же третьем классе. Этот класс называется суммой классов.
Коммутативность 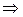 из (2), а ассоциативность доказывается прямыми вычислениями.
из (2), а ассоциативность доказывается прямыми вычислениями.
Дроби вида 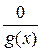 равны между собой и образуют нулевой класс. Это нуль относительно сложения. Действительно,
равны между собой и образуют нулевой класс. Это нуль относительно сложения. Действительно, 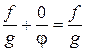 . Из равенства
. Из равенства  противоположного класса.
противоположного класса.
Умножение определим формулой
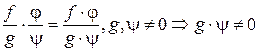
| (3)
|
Пусть 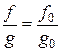 ,
, 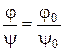
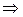
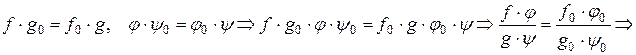 можно говорить о произведении классов равных между собой дробей.
можно говорить о произведении классов равных между собой дробей.
Коммутативность и ассоциативность 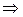 из (3), а дистрибутивность доказывается прямыми вычислениями.
из (3), а дистрибутивность доказывается прямыми вычислениями.
Элементы вида 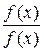 обозначают единицу.
обозначают единицу.
Если  нулевому классу, т.е.
нулевому классу, т.е.  определён класс
определён класс 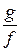 - обратный класс к
- обратный класс к 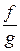 . Т.о. классы равных между собой рациональных дробей с коэффициентами из P образуют поле, обозначаемое P(x) – поле рациональных дробей.
. Т.о. классы равных между собой рациональных дробей с коэффициентами из P образуют поле, обозначаемое P(x) – поле рациональных дробей.
Многочлены – подмножество 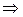
 − кольцо.
− кольцо.
Замечание. Аналогично над кольцом Z.
Определение 3. Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя.
Замечание. Дроби вида 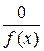 являются правильными.
являются правильными.
Лемма 2. Всякая рациональная дробь представима, притом единственным способом, в виде суммы многочлена и правильной дроби.
Доказательство. Пусть дана рациональная дробь 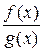 . Разделим
. Разделим  на
на 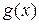 :
:
 , где
, где 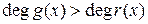
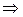
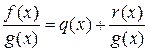 . Если наряду с полученным равенством имеет место
. Если наряду с полученным равенством имеет место 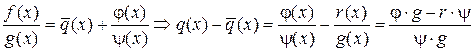 . Слева – многочлен, справа – правильная дробь
. Слева – многочлен, справа – правильная дробь 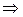
 , что и требовалось доказать. ■
, что и требовалось доказать. ■
Напоминание. Над 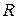 неприводимые многочлены имеют вид:
неприводимые многочлены имеют вид: 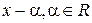 , и
, и 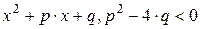 , т.е.
, т.е.  Над
Над 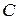 , неприводимые многочлены
, неприводимые многочлены  .
.
Определение 4. Правильная рациональная дробь 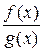 называется простейшей, если её знаменатель
называется простейшей, если её знаменатель 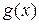 является степенью неприводимого многочлена
является степенью неприводимого многочлена  , т.е.
, т.е. 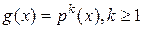 , и
, и  .
.
Теорема 1. Всякая правильная дробь разлагается в сумму простейших.
Доказательство. Вначале рассмотрим правильную рациональную дробь 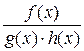 , где
, где 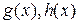 − взаимно простые, т.е.
− взаимно простые, т.е. 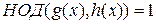 . Тогда найдутся многочлены
. Тогда найдутся многочлены  такие, что
такие, что  . Отсюда
. Отсюда  .
.
Пусть, деля  на
на  , получим остаток
, получим остаток  такой, что
такой, что  (4), где
(4), где 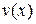 − многочлен. Так как
− многочлен. Так как 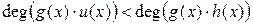 и
и  . Из (4) следует, что
. Из (4) следует, что  , где справа стоит сумма правильных дробей.
, где справа стоит сумма правильных дробей.
Если хотя бы один из знаменателей 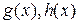 разлагается в произведение взаимно простых множителей, то можно выполнить дальнейшее разложение. Продолжая далее, получаем, что всякая правильная дробь разлагается в сумму нескольких простейших дробей, каждая из которых имеет знаменателем степень некоторого неприводимого многочлена. А именно, если для
разлагается в произведение взаимно простых множителей, то можно выполнить дальнейшее разложение. Продолжая далее, получаем, что всякая правильная дробь разлагается в сумму нескольких простейших дробей, каждая из которых имеет знаменателем степень некоторого неприводимого многочлена. А именно, если для 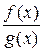 имеем, что
имеем, что  , где
, где 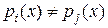 , если
, если 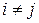 , то
, то
 , где справа стоят правильные дроби.
, где справа стоят правильные дроби.
Осталось рассмотреть 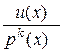 , где это правильная дробь, p(x) – неприводимый многочлен. Применим алгоритм деления с остатком и разделим
, где это правильная дробь, p(x) – неприводимый многочлен. Применим алгоритм деления с остатком и разделим  на
на  , остаток разделим на
, остаток разделим на 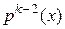 , и т.д. Имеем:
, и т.д. Имеем:

Так как степень  меньше чем у
меньше чем у  , а степень каждого из остатков
, а степень каждого из остатков  меньше
меньше 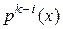 , то степень всех частных
, то степень всех частных 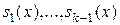 меньше, чем степень
меньше, чем степень  . Степень последнего остатка
. Степень последнего остатка  меньше, чем
меньше, чем  откуда следует, что
откуда следует, что 
 получаем:
получаем:
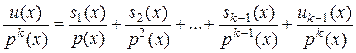 , т.е. получено искомое представление. ■
, т.е. получено искомое представление. ■
Следствие. Всякая правильная рациональная дробь обладает единственным разложением в сумму простейших дробей.
Доказательство. Пусть это неверно. Тогда вычитая из одного разложения другое, получаем поле приведения подобных в сумму простейших дробей, тождественно равную нулю. Пусть простейшие дроби содержат неприводимые многочлены 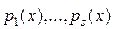 , причём максимальная степень каждого
, причём максимальная степень каждого  соответственно. Умножим всю сумму на
соответственно. Умножим всю сумму на  . Тогда все слагаемые, кроме одного – многочлены и осталось
. Тогда все слагаемые, кроме одного – многочлены и осталось  . Так как
. Так как 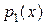 - неприводим, то числитель не делится на знаменатель, а все множители с ним взаимно просты
- неприводим, то числитель не делится на знаменатель, а все множители с ним взаимно просты 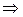 противоречие, т.к. нуль представлен в виде суммы многочлена и правильной дроби. ■
противоречие, т.к. нуль представлен в виде суммы многочлена и правильной дроби. ■
Пример.
Представить 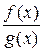 в виде суммы простейших дробей, где:
в виде суммы простейших дробей, где:
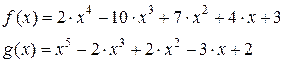
Решение.
Здесь 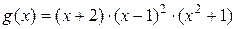 и
и 


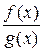 , где
, где 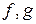 − многочлены. Мы их будем рассматривать как формальные выражения. При этом используем обычные операции:
− многочлены. Мы их будем рассматривать как формальные выражения. При этом используем обычные операции: , где
, где 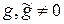 ;
; 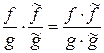 ;
;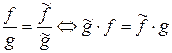 .
.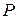 – поле,
– поле,  – кольцо многочленов над
– кольцо многочленов над 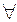 паре многочленов
паре многочленов  , где
, где 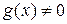 поставим в соответствие символ
поставим в соответствие символ  и знаменателем
и знаменателем 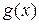 .
.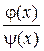 называются равными, если в кольце
называются равными, если в кольце 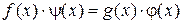 .
.
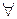 дробь равна самой себе.
дробь равна самой себе. и
и 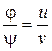
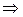
 .
. ,
, 
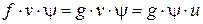 . Далее после деления на
. Далее после деления на  получим доказываемое равенство, т.к.
получим доказываемое равенство, т.к.  и можно разделитьна
и можно разделитьна 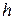 , то получаем, что операция не выводит из класса.■
, то получаем, что операция не выводит из класса.■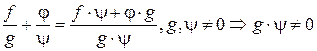
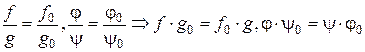 ,
,  , а второе на
, а второе на  и складывая |
и складывая | 
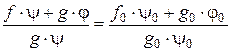
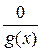 равны между собой и образуют нулевой класс. Это нуль относительно сложения. Действительно,
равны между собой и образуют нулевой класс. Это нуль относительно сложения. Действительно, 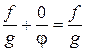 . Из равенства
. Из равенства  противоположного класса.
противоположного класса.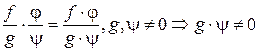
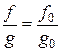 ,
, 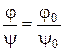
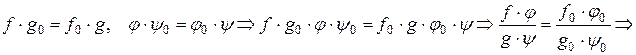 можно говорить о произведении классов равных между собой дробей.
можно говорить о произведении классов равных между собой дробей.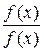 обозначают единицу.
обозначают единицу. нулевому классу, т.е.
нулевому классу, т.е.  определён класс
определён класс 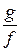 - обратный класс к
- обратный класс к 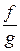 . Т.о. классы равных между собой рациональных дробей с коэффициентами из P образуют поле, обозначаемое P(x) – поле рациональных дробей.
. Т.о. классы равных между собой рациональных дробей с коэффициентами из P образуют поле, обозначаемое P(x) – поле рациональных дробей. − кольцо.
− кольцо.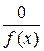 являются правильными.
являются правильными. , где
, где 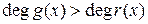
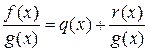 . Если наряду с полученным равенством имеет место
. Если наряду с полученным равенством имеет место 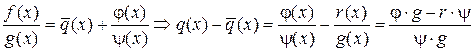 . Слева – многочлен, справа – правильная дробь
. Слева – многочлен, справа – правильная дробь  , что и требовалось доказать. ■
, что и требовалось доказать. ■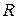 неприводимые многочлены имеют вид:
неприводимые многочлены имеют вид: 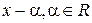 , и
, и 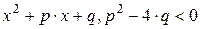 , т.е.
, т.е.  Над
Над 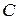 , неприводимые многочлены
, неприводимые многочлены  .
. , т.е.
, т.е. 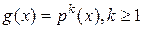 , и
, и  .
.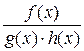 , где
, где 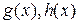 − взаимно простые, т.е.
− взаимно простые, т.е. 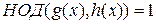 . Тогда найдутся многочлены
. Тогда найдутся многочлены  такие, что
такие, что  . Отсюда
. Отсюда  .
. на
на  , получим остаток
, получим остаток  такой, что
такой, что  (4), где
(4), где 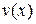 − многочлен. Так как
− многочлен. Так как 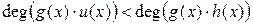 и
и  . Из (4) следует, что
. Из (4) следует, что  , где справа стоит сумма правильных дробей.
, где справа стоит сумма правильных дробей. , где
, где 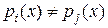 , если
, если 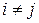 , то
, то , где справа стоят правильные дроби.
, где справа стоят правильные дроби.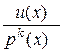 , где это правильная дробь, p(x) – неприводимый многочлен. Применим алгоритм деления с остатком и разделим
, где это правильная дробь, p(x) – неприводимый многочлен. Применим алгоритм деления с остатком и разделим  , остаток разделим на
, остаток разделим на 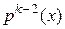 , и т.д. Имеем:
, и т.д. Имеем:
 , а степень каждого из остатков
, а степень каждого из остатков  меньше
меньше 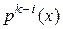 , то степень всех частных
, то степень всех частных 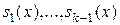 меньше, чем степень
меньше, чем степень  меньше, чем
меньше, чем 
 получаем:
получаем: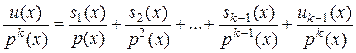 , т.е. получено искомое представление. ■
, т.е. получено искомое представление. ■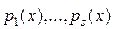 , причём максимальная степень каждого
, причём максимальная степень каждого  соответственно. Умножим всю сумму на
соответственно. Умножим всю сумму на  . Тогда все слагаемые, кроме одного – многочлены и осталось
. Тогда все слагаемые, кроме одного – многочлены и осталось  . Так как
. Так как 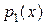 - неприводим, то числитель не делится на знаменатель, а все множители с ним взаимно просты
- неприводим, то числитель не делится на знаменатель, а все множители с ним взаимно просты 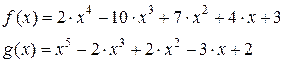
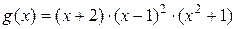 и
и 




