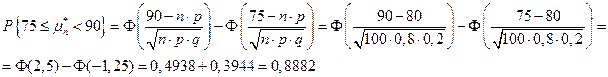Дисперсия. Дисперсия – какой разброс имеют возможные значения случайной величины от математического ожидания.
Дисперсия – какой разброс имеют возможные значения случайной величины от математического ожидания. Введём случайную величину
Затем решили перейти к Определение. Дисперсией случайной величины называется математическое ожидание квадрата соответствующей центрированной случайной величины.
Формулы для вычисления дисперсии: 1) дискретная случайная величина 2) непрерывная случайная величина Дисперсия имеет размерность квадрата случайной величины. Для наглядной оценки рассеивания удобно пользоваться характеристикой, размерность которой совпадает с размерностью случайной величины.
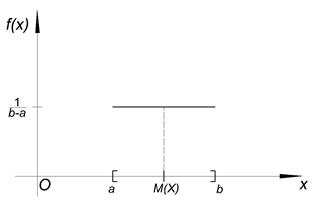
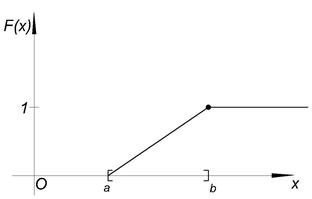
Математическое ожидание и дисперсия характеризуют наиболее важные черты распределения случайной величины – его расположение и степень разбросанности. Свойства дисперсии: 1°. 2°. 3°. Если X, Y – независимые случайные величины, то Примеры непрерывных случайных величин. 1. Равномерно распределённая на [ a, b ] случайная величина Х. Опыт: на отрезок [ a, b ] бросается точка
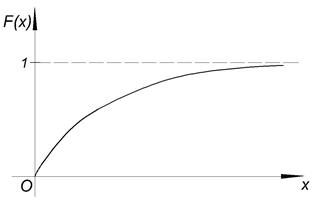
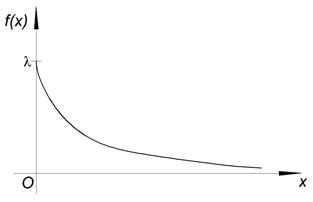
2. Показательное распределение.
§6. Нормальный закон распределения случайной величины.
Это наиболее часто встречающийся на практике закон распределения.
Убедимся в том, что а – математическое ожидание, а σ; – среднее квадратическое отклонение нормального распределения ( 1) Будем вычислять интеграл методом замены переменной
Замена
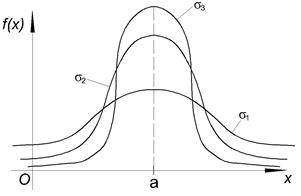
§7. Функция плотности, кривая Гаусса.
§8. Вероятность попадания на заданный интервал нормальной случайной величины.
Замена
Пример. Случайная величина подчинена нормальному закону
a =30; σ;=10, найти
§9. Вероятность заданного отклонения.
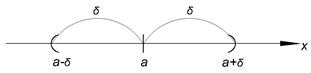
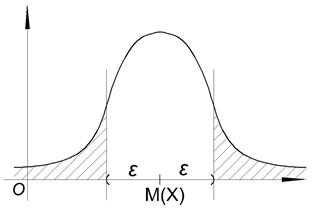
Пусть δ;>0 – заданное положительное число. Найти
§10. Правило трёх сигм.
Положим δ=3σ, найдём
Если случайная величина распределена нормально, то абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения. На практике правило используют так: если распределение неизвестно, но выполняется это правило, то есть основания предполагать, что случайная величина распределена нормально.
Предельные теоремы теории вероятностей устанавливают закономерности при массовом проявлении случайных явлений. Нельзя предсказать исход отдельного случайного явления, но оказывается, что средний результат массы случайных явлений является закономерным и может быть предсказан с большой степенью определённости.
§11. Закон больших чисел.
Закон больших чисел – это совокупность теорем, которые устанавливают с вероятностью как угодно близкой к единице, что наступит некоторое событие, зависящее от неограниченного увеличивающегося числа случайных факторов. Влияние каждого фактора мало по сравнению с суммарным действием всех факторов. Пусть дана последовательность случайных величин:
Говорят, что последовательность (1) удовлетворяет закону больших чисел, если т.е. с вероятностью, как угодно близкой к единице наступит событие, состоящее в том, что уклонение среднего арифметического достаточно большого числа случайных величин от среднего арифметического их математических ожиданий будет сколь угодно малым по абсолютной величине.
§12. Неравенство Чебышёва.
Даёт оценку вероятности больших уклонений случайной величины от математического ожидания. Х - случайная величина, D (X) – дисперсия, Доказательство. (проведём для непрерывной случайной величины)
§13. Теорема Чебышёва.
x1, x2, …, xn, … (1) 1. Случайные величины Xk – попарно независимы. 2. Дисперсии этих случайных величин равномерно ограничены: Тогда (1) удовлетворяет закону больших чисел. Доказательство. Рассмотрим случайную величину
Тогда запишем для этой случайной величины неравенство Чебышёва
§14. Теорема Бернулли.
Это частный случай теоремы Чебышёва. Производится n независимых опытов, каждый опыт имеет 2 исхода: успех – p, неудача – q.
Утверждение теоремы: Доказательство. Теорема сразу следует из теоремы Чебышёва, если заметить, что случайную величину
Докажем, что в этом случае выполняются условия теоремы Чебышёва: 1) xk – попарно независимы 2) дисперсии равномерно ограничены
Последовательность случайных величин x1 + x2 +…+ xn удовлетворяет всем условиям теоремы Чебышёва, поэтому она удовлетворяет закону больших чисел (*).
§15. Центральная предельная теорема.
Общий смысл центральной предельной теоремы заключается в следующем: если случайная величина представляет собой сумму слабо зависимых слагаемых и каждое слагаемое невелико по сравнению со всей суммой, то независимо от природы этих слагаемых, т.е. от того, какой они имеют закон распределения, с ростом числа слагаемых распределение этой случайной величины сближается с нормальным законом.
§16. Теорема Муавра-Лапласа.
Пусть производится n независимых опытов, каждый опыт имеет 2 исхода:
Рассмотрим случайную величину Утверждение теоремы:
(1) Вероятность попадания случайной величины Без доказательства. Нормальная сумма:
поэтому равенство (1) можно записать более подробно
Пример. Произведено 100 независимых испытаний (n =100), p =0,8. Найти вероятность того, что случайная величина
|


 - центрированная случайная величина.
- центрированная случайная величина.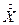 нельзя взять за характеристику рассеяния возможных значений, т.к.
нельзя взять за характеристику рассеяния возможных значений, т.к. 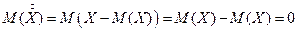 .
.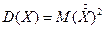 - дисперсия.
- дисперсия.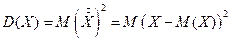
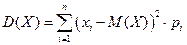
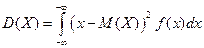
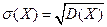 - среднее квадратическое отклонение случайной величины.
- среднее квадратическое отклонение случайной величины.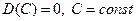 .
.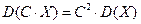 .
. .
.
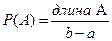
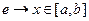
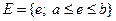
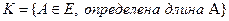
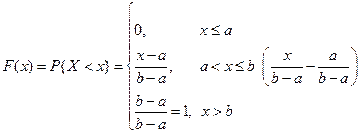
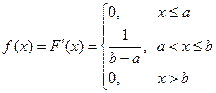
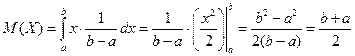
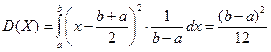
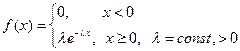
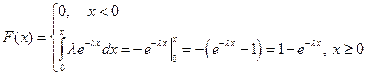
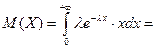
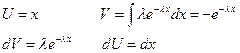
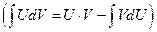

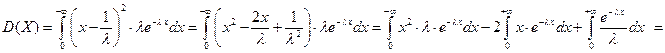
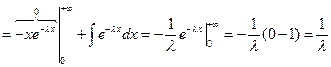
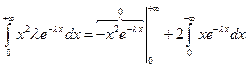
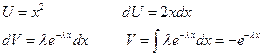




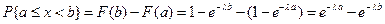
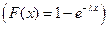
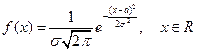 - это распределение также называется законом Гаусса.
- это распределение также называется законом Гаусса.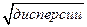 ).
).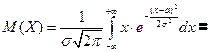
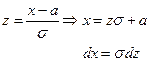 пределы интегрирования не меняются, т.к. замена линейная.
пределы интегрирования не меняются, т.к. замена линейная.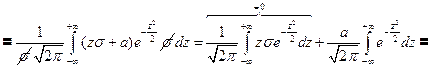
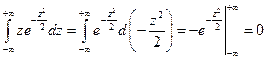
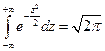 - неберущийся интеграл, интеграл Эйлера-Пуассона
- неберущийся интеграл, интеграл Эйлера-Пуассона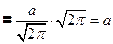
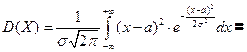
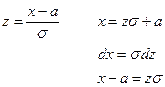
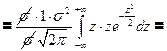
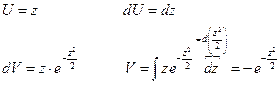
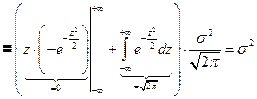
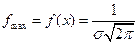
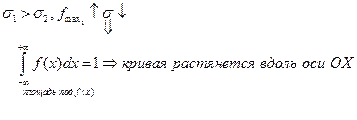 Если σ;=1, a =0, то
Если σ;=1, a =0, то 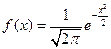 случайная величина имеет стандартное нормальное распределение.
случайная величина имеет стандартное нормальное распределение.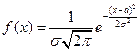
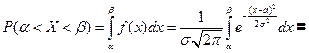

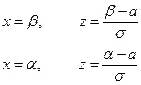
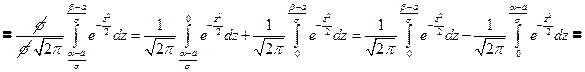
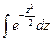 - неберущийся, т.е. не выражается через элементарные функции, пользуются табл. спец. функции, функцией Лапласа или интегралом вероятности:
- неберущийся, т.е. не выражается через элементарные функции, пользуются табл. спец. функции, функцией Лапласа или интегралом вероятности:  .
.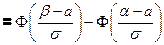 .
.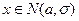
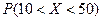 .
.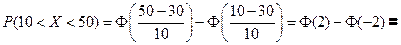
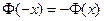
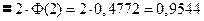 .
.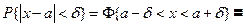
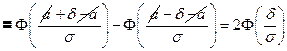
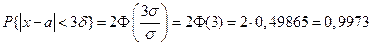

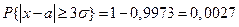
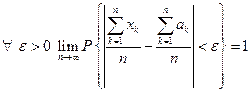 ,
,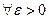 , тогда
, тогда 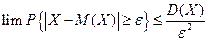 .
.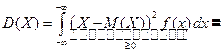
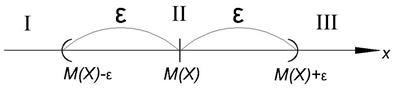

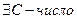 :
: 
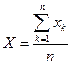
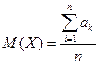
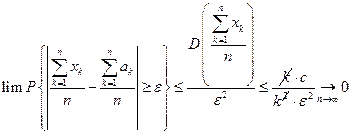
 .
.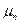 - суммарное число успехов за n испытаний.
- суммарное число успехов за n испытаний.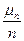 - частота успеха.
- частота успеха.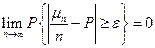 (*)
(*)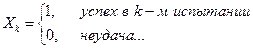
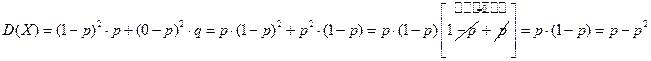

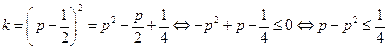
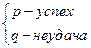
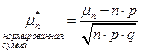
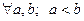
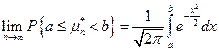
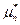 на (a, b) считается для нормальной случайной величины.
на (a, b) считается для нормальной случайной величины.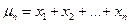
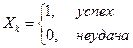
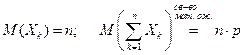
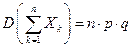 ,
,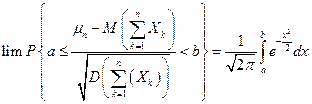 .
.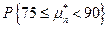 .
.