Применение графиков в решении уравненийУравнением с одним неизвестным называется равенство f (x) = g (x), в котором требуется найти неизвестную величину x. Пусть задано квадратное уравнение x 2 + рх + q = 0. Перепишем его следующим образом: х 2 = – рх – q и построим графики зависимостей y = x2 и y = – рх – q. График первой зависимости известен – это парабола; вторая зависимость – линейная. В том случае, когда х является решением уравнения, координаты точек обоих графиков равны между собой. Если прямая и парабола пересекаются, то абсциссы гочек пересечения являются корнями квадратного уравнения. Пример 3.1. Решить уравнение 4х2 –12 х + 7 = 0. Представим уравнение в виде х2 = 3 х – 7/4. Построим параболу у = х2 и прямую у = 3 х – 7/4 (рисунок 3.1). Парабола и прямая пересекаются в двух точках с абциссами x 1 = 0.8 и х 2 = 2.2.
Рисунок 3.1 – Графическое решение уравнения
Пример 3.2. Решить уравнение х2 – х + 1 = 0. Запишем уравнение в виде х 2 = х – 1. Построив параболу у = х2 и прямую у= х – 1 (рисунок 3.2), увидим, что их графики не пересекаются (рисунок 3.2) – значит, уравнение не имеет действительных корней.
Рисунок 3.2 – Графическое решение уравнения
Пример 3.3. Решить систему уравнений Построим в одной системе координат графики уравнений (рисунок 3.3): x 2 + y 2 = 25 и y = – x 2 + 2 x + 5.
Рисунок 3.3 – Графическое решение уравнения
Координаты любой точки построенной окружности являются решением первого уравнения, а координаты любой точки параболы – решением второго уравнения. Значит, координаты каждой из точек пересечения окружности и параболы удовлетворяют как первому уравнению системы, так и второму, т. е. являются решением рассматриваемой системы. Находим приближённые значения координат точек пересечения графиков: А(–2.2; –4.5), В(0; 5), С (2.2; 4.5), D (4; –3). Следовательно, система уравнений имеет четыре решения:
Подставив найденные значения в уравнения системы, можно убедиться, что второе и четвёртое из этих решений являются точными, а первое и третье – приближёнными. Пример 3.4. Решить уравнение sin x + cos x = 1. Тригонометрические уравнения решают как аналитически, так и графически. Рассмотрим графический способ решения на примере рисунка 3.4.
Рисунок 3.4 – Графическое решение уравнения
Построим графики функций y = sin x и y = 1 – cos x. Из графика видно, что уравнение имеет две корней: x = 2π· n, где [kgl].
[gl] Тема 4. Алгебраические уравнения. Диофантово уравнение [:]
Уравнение – аналитическая запись задачи о разыскании значений аргументов, при которых значения двух данных функций равны f (x, y,...) = g (x, у,...). Аргументы, от которых зависят эти функции, называются обычно неизвестными, а значения неизвестных, при которых значения функций равны, – решениями или корнями. О таких значениях неизвестных говорят, что они удовлетворяют данному уравнению. Алгебраические уравнения имеют следующий вид: P (x 1, …, xn) = Q (x 1, …, xn), где Р и Q – многочлены с коэффициентами из поля рациональных чисел. Линейное уравнение – это уравнение, обе части которого могут быть выражены многочленами (от неизвестных) первой степени. Линейное уравнение можно привести к виду: ах+b = 0, где а – ненулевой параметр, b – произвольный параметр. Линейное уравнение имеет единственное решение Квадратное уравнение – уравнение вида ах2 + bх + с = 0, где а ≠ 0. В общем случае уравнение решается так:
Число D = b2 – 4ас называется дискриминантом многочлена ах2 + bх + с = 0. Если D > 0, то уравнение имеет два различных вещественных корня. Если D = 0, то оба корня вещественны и равны. Если D < 0, то оба корня являются комплексными сопряжёнными числами. Квадратное уравнение вида x 2 + px + q = 0, в котором ведущий коэффициент (т. е. коэффициент при старшем члене) равен единице, называют приведённым. В этом случае решение такого уравнения выглядит следующим образом:
Теорема Виета. Сумма корней приведённого квадратного уравнения x 2 + px + q = 0 равна коэффициенту p, взятому с противоположным знаком, а произведение корней равно свободному члену q: x 1 + x 2 = – p; x 1· x 2 = q. В случае неприведённого квадратного уравнения ах2 + bх + с = 0:
Кубическое уравнение – уравнение вида ах3 + bх2 + сx + d = 0, где a ≠ 0. Заменяя в этом уранении x новым неизвестным y, связанным с x равенством y 3 + py + q = 0. где
Решение этого уравнения можно получить с помощью формулы Кардано. Пример 4.1. Решить уравнение Решение Возведём обе части этого уравнения в квадрат и получим x2 – 5 = 4, откуда следует, что x2 = 9, т. е. x 1,2 = ±3. Проверим, что полученные числа являются решениями уравнения. Действительно, при подстановке их в данное уравнение получаются верные равенства:
Следовательно, х1 = 3 или х2 = –3 – решения данного уравнения. Пример 4.2. Решить уравнение Решение Возведём в квадрат обе части уравнения, получим x = x 2 – 4 x + 4. После преобразований приходим к квадратному уравнению х2 – 5х + 4 = 0, корни которого х 1 = 1 и х2 = 4. Проверим, являются ли найденные числа решениями данного уравнения. При подстановке в него числа 4 получим верное равенство Ответ: х = 4. Пример 4.3. Решить уравнение
|

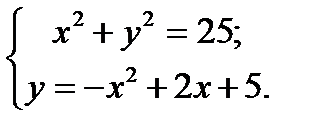
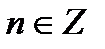 и x = π/2 + 2π· k, где
и x = π/2 + 2π· k, где 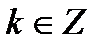 .
.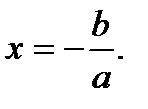
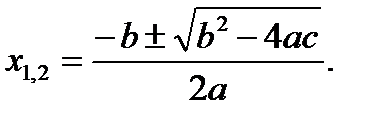
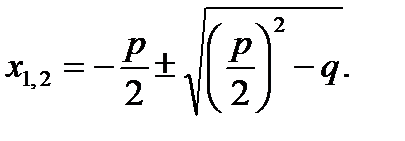
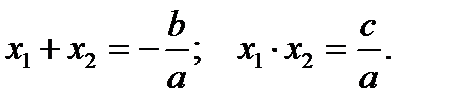
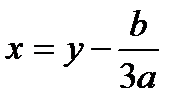 , уравнение можно привести к более простому (каноническому) виду:
, уравнение можно привести к более простому (каноническому) виду: .
.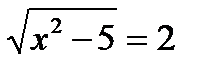 .
. и
и  .
.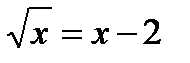 .
.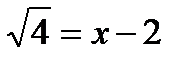 , т. е. 4 – решение данного уравнения. При подстановке же числа 1 получаем в правой части –1, а в левой части число 1. Следовательно, 1 не является решением уравнения; говорят, что это посторонний корень, полученный в результате принятого способа решения.
, т. е. 4 – решение данного уравнения. При подстановке же числа 1 получаем в правой части –1, а в левой части число 1. Следовательно, 1 не является решением уравнения; говорят, что это посторонний корень, полученный в результате принятого способа решения. .
.


