Передаточная функция, соответствующая уравнению (1), имеет вид
т.е. по динамическим свойствам термометр является инерционным звеном второго порядка. Коэффициент передачи (чувствительность) К и постоянные времени T22 и T1 - это параметры математической модели, подлежащие определению при выполнении лабораторной работы. Если быстро перенести датчик - термоэлектрический преобразователь из нагретого термошкафа в сосуд с холодной водой, то его входная величина - температура q изменится ступенчато от начального значения qндо конечного значения qк, а выходная величина термометра - показания прибора N - будет изменяться значительно медленнее. Записанные на диаграмме потенциометра показания, изменяющиеся от начального значения Nндо конечного значения Nк, будут представлять собой кривую разгона термометра. При построении графика изменения во времени входной температуры и кривой разгона принято показывать не текущие значения входной и выходной величин qiи Ni, а их отклонения от начальных значений: Dqi= qi- qн; DNi= Ni– Nн. При этом максимальные значения отклонений будут равны: Dq0= qк- qн; DNуст= Nк– Nн. Для термоэлектрического термометра изменение показаний на выходе после окончания переходного процесса (новое установившееся значение DNуст) будет равно по размеру ступенчатому изменению температуры на входе Dq0, поэтому коэффициент передачи (чувствительность) термометра К=1 ОС/ОС. Одним из методов определения значений параметров математической модели динамики термометра по его кривой разгона является "метод площадей", изложенный в монографии [3]. В соответствии с ним ось абсцисс над кривой разгона необходимо разбить на n равных по длине отрезков с интервалом времени Dt - так, чтобы на этих интервалах кривая разгона мало отличалась от прямой линии. В графу 1 таблицы 1 необходимо занести значения моментов времени ti, при этом t0 = 0, t1 = Dt, t2 = 2Dt и т.д. В графу 2 нужно записать отклонения показаний прибора DNiот начального значения в конце каждого интервала. Затем значения отклонений DNi в конце каждого интервала следует разделить на установившееся значение DNусти полученные значения
занести в графу 3 таблицы 1. Таблица 1 - Промежуточные результаты расчетов
В графу 4 таблицы 1 требуется записать значения разностей [1-s(i×Dt)]. После этого может быть рассчитано значение постоянной времени Т1 по формуле
Затем необходимо ввести новую безразмерную переменную Q = t/T1, рассчитать значения произведений i×DQ и разностей (1- i×DQ), в которых DQ=Dt/T1, и записать их в графу 6 таблицы 1. Далее нужно рассчитать значения произведений [1-s(i×Dt)](1- i×DQ) и записать результаты в графу 7 таблицы 1. После этого может быть рассчитано значение постоянной времени T22 по формуле
Проверка адекватности математической модели динамики термометра проводится сравнением ординат кривой разгона и переходной характеристики, являющейся решением уравнения (1), при значении входной величины Dq(t) = Dqо= q к- q н. Вид переходной характеристики зависит от вида корней характеристического уравнения
Для термоэлектрического термометра корни характеристического уравнения будут отрицательными вещественными. Если обозначить их как
Если корни равны конкретным значениям
|

 (2)
(2) (3)
(3)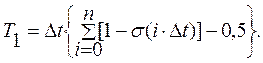 (4)
(4) (5)
(5) (6)
(6) тогда переходная функция может быть записана
тогда переходная функция может быть записана (7)
(7) .
.


