Общая задача приближения по методу наименьших квадратов.Пусть Обобщенным полиномом m-й степени Pm(x) будем называть выражение следующего вида:
где a0, a1, a2, …, am – произвольные постоянные. Дадим обобщение результатов предшествующих двух пунктов в применении к приближению в смысле среднеквадратического при помощи обобщенных полиномов. При этом мы ограничимся случаем непрерывного аргумента (промежутка), так как случай ряда дискретных точек может быть рассмотрен по аналогии. Ставим следующую задачу. Требуется подобрать такие значения коэффициентов a0, a1, a2, …, am в обощенном полиноме (7), чтобы интеграл
т.е.
принял наименьшее значение. Приравнивая нулю частные производные интеграла I по всем ak получим следующую систему уравнений:
или
Систему (9) можно записать в компактном виде:
где введем следующие обозначения:
Определитель системы (9) запишем в виде:
Определитель (12) есть определитель Грамма. Следовательно, Система (9), а также вычисления, связанные с ее решением значительно упрощаются, в том случае, когда система функций
Система (9) в этом случае дает:
Числа ak, определяемые по формуле (14), называются коэффициентами Фурье функции f(x) относительно ортогональной системы функций В качестве примера ортогональной системы функций можно указать систему тригонометрических функций 1, cos x, sin x, cos 2x, sin 2x, …, cos mx, sin mx, ортогональную на отрезке
Отметим, что по аналогии со случаем приближения при помощи степенных многочленов в некоторых случаях вместо интеграла (8) рассматривают интеграл более общего вида:
где Система функций
Коэффициенты обобщенного полинома будут определяться равенствами:
При приближении функции по способу наименьших квадратов в качестве системы функций В этих случаях обощенный полином Pm(x) в конечном счете сводится к обыкновенному степенному полиному. В качестве примера рассмотрим случаи полиномов Лежандра и полиномы Чебышева. n-й полином Лежандра модно определить следующей формулой:
Полагая n=0,1,…,5 получим первые шесть полиномов Лежандра:
Используя формулу (19), интегрированием по частям можно убедиться в справедливости равенств:
Таким образом, полиномы Лежандра образуют ортогональную систему полиномов на отрезке [-1;1]. Полиномы Чебышева Tn(x) определяется равенством:
где По формуле (22) получим первые шесть полиномов Чебышева:
Непосредственным подсчетом можно убедиться, что:
т.е. полиномы Чебышева образуют на отрезке [-1;1] ортогональную систему полиномов с весом Пример. Требуется аппроксимировать функцию Для аппроксимации с весом
где ak согласно (14) и (21) определяются равенствами:
Подставляя сюда многочлены Lk(x) из (20), непосредственным подсчетом получаем:
Для аппроксимации с весом
Коэффициенты ak согласно (14) и (24) определяются равенствами:
Подставляя сюда Tk(x) из (23), получаем:
и Отметим, что приближение, получаемое с помощью полиномов Чебышева, учитывает, в большей степени значения приближаемой функции у концов отрезка [-1;1]; а приближение, получаемое с помощью полиномов Лежандра, учитывает все значения приближаемой функции в промежутке [-1;1] в одинаковой степени.
|

 - заданная на отрезке [a,b] система линейно независимых и непрерывных функций.
- заданная на отрезке [a,b] система линейно независимых и непрерывных функций. (7)
(7) (8)
(8)

 (9)
(9) (10)
(10) (11)
(11) (12)
(12) , т.к. система
, т.к. система 
 ортогональна на отрезке [a,b], то есть имеют место равенства:
ортогональна на отрезке [a,b], то есть имеют место равенства: при
при  . (13)
. (13)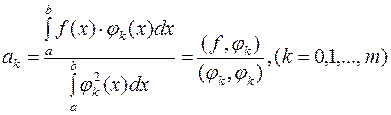 . (14)
. (14) , так как интегрированием легко показать справедливость следующих равенств:
, так как интегрированием легко показать справедливость следующих равенств: (15)
(15) при
при  (16)
(16) - функция, такая же, как и в (6’).
- функция, такая же, как и в (6’). при
при  (18)
(18) (19)
(19) (20)
(20) (21)
(21) (22)
(22) (целое).
(целое). (23)
(23) при
при 
 (24)
(24)
 на отрезке [-1;1] полиномом четвертой степени с весом
на отрезке [-1;1] полиномом четвертой степени с весом  а также с весом
а также с весом  .
.









