РАЗДЕЛ 1. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИОсновные формулы
Кинематика поступательного движения
1. Скорость при прямолинейном движении в общем случае
V 2 = Vx2 + Vy2 + Vz2.
2. Ускорение
a 2 = ax2 + ay2 + az2
3. Уравнения кинематики равноускоренного поступательного движения: V = V0 + a ×t, S = V0 t + a ×t2/2, где V – скорость тела в момент времени t; V0 – начальная скорость; a – ускорение движения тела; S – путь, пройденный за время t; t – время движения тела. 4. Полное ускорение при криволинейном движении a2 = at2 + an2, где aτ = dV/dt – тангенциальное ускорение; an = V2/R – нормальное ускорение.
Кинематика вращательного движения
5. Угловая скорость при вращательном движении в общем случае
6. Угловое ускорение
7. Уравнения кинематики равноускоренного вращательного движения: ω = ω0 + e t, j = ω0 t + e t2/2, где ω; – угловая скорость в момент времени t; ω0 – начальная угловая скорость; e – угловое ускорение, с которым вращается тело; t – время вращения тела; j – угол поворота за время t. 8. Угловая скорость при равномерном вращательном движении ω = j/t = 2π/T = 2π ν, где T – период обращения; ν; – частота обращения, т. е. число оборотов в единицу времени. 9. Формулы, связывающие угловые и линейные величины при рассмотрении движения вращающегося тела: S = j R, V = ω R, аt = e R, an = ω 2 R = V2/R, где R – радиус траектории, по которой движется тело; at – тангенциальное ускорение; an – нормальное или центростремительное ускорение.
|

 = Vx
= Vx  + Vy
+ Vy  + Vz
+ Vz  ,
,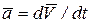 = ax
= ax 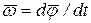 .
. .
.


