Интегрирование рациональных дробей
Задача интегрирования рациональной дроби сводится к умению интегрирования только правильных рациональных дробей, так как интегрирование целой части дроби (многочлена) не сложная. Если решена задача разложения правильной дроби на сумму простых дробей, то дальше надо уметь интегрировать простые дроби. Покажем, как интегрировать такие дроби. I. II.
III.
Интегрирование дроби IV типа проводится аналогично интегрированию дроби III типа. Пример 22.
[ D = 16 – 52 < 0 Þ дробь III типа.]
Ответ: Пример 23.
Ответ:
Итак, любая рациональная дробь интегрируема. Для этого необходимо выполнить следующие действия. 1) Если дробь является неправильной, выделить ее целую часть. То есть представить в виде:
где Tm-n (x) и Rr (x) – многочлены степени m-n и r соответственно (причем r<n). 2) Разложить правильную рациональную дробь 3) Вычислить интегралы от многочлена Tm-n (x) и каждой из простых дробей, полученных на шаге 2). Пример 24. 1) Дробь
Поэтому можно записать:
2) Полученную правильную дробь
Отсюда следует: Значит, подынтегральная рациональная дробь представима в виде:
3) Найдем интеграл:
Ответ:
|
,
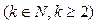
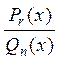на сумму простых дробей
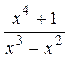- неправильная рациональная дробь. Выделим ее целую часть:
разложим на сумму простых дробей:
